[백준(python)] 2042번 : 구간 합 구하기

이번 문제는 지난번 문제에 이어 구간트리를 이용해보는 실전 문제이다.

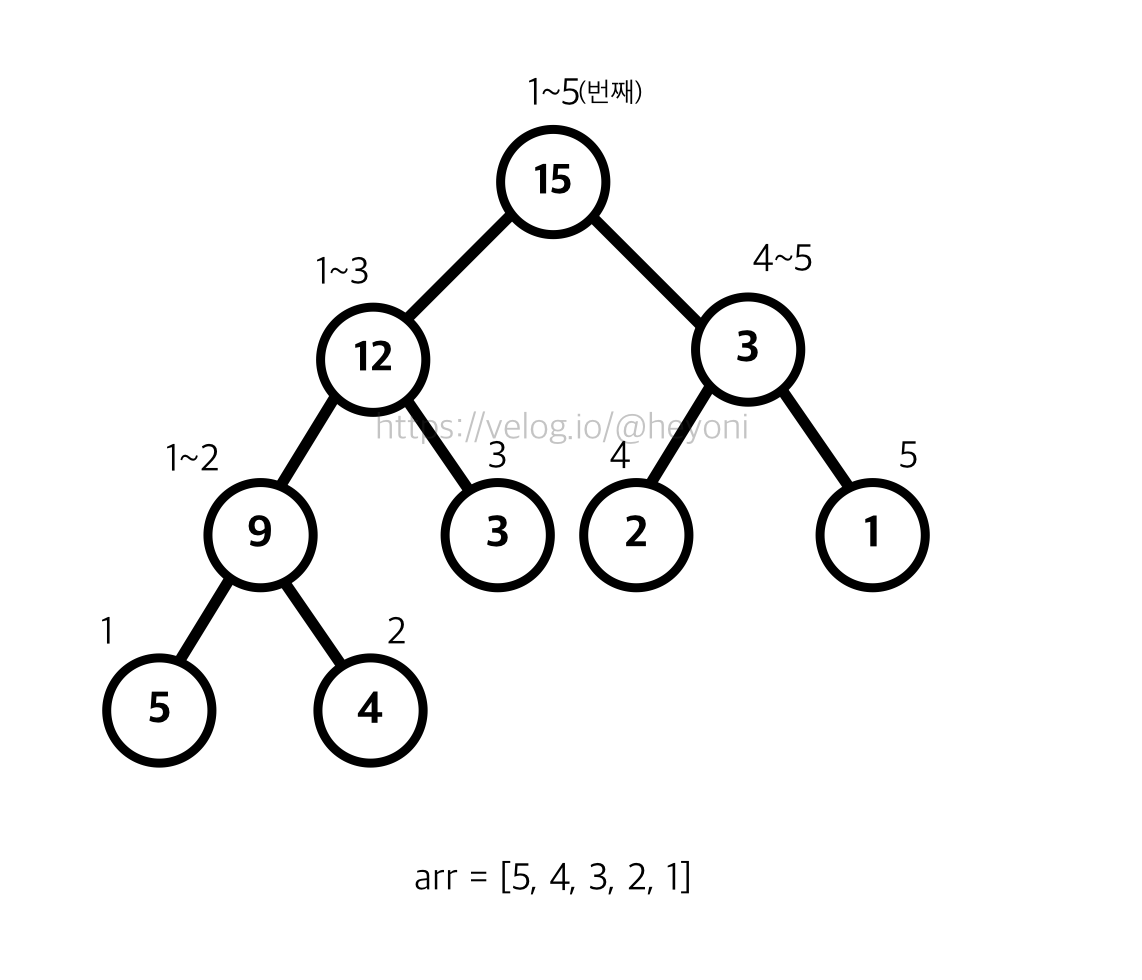
지난번 알고리즘 풀이에서 설명했던 사진을 그대로 가져왔다.
*사진에서 노드 위에 붙어있는 숫자는 우리가 일반적으로 사용하는 순서(1번째, 2번째...)이다. 개발자들이 사용하는 0부터 시작하는 순서가 아님!

여기서 세그먼트 트리를 만들기 위해 풀어보자면, 아래와 같은 사진이 나온다.

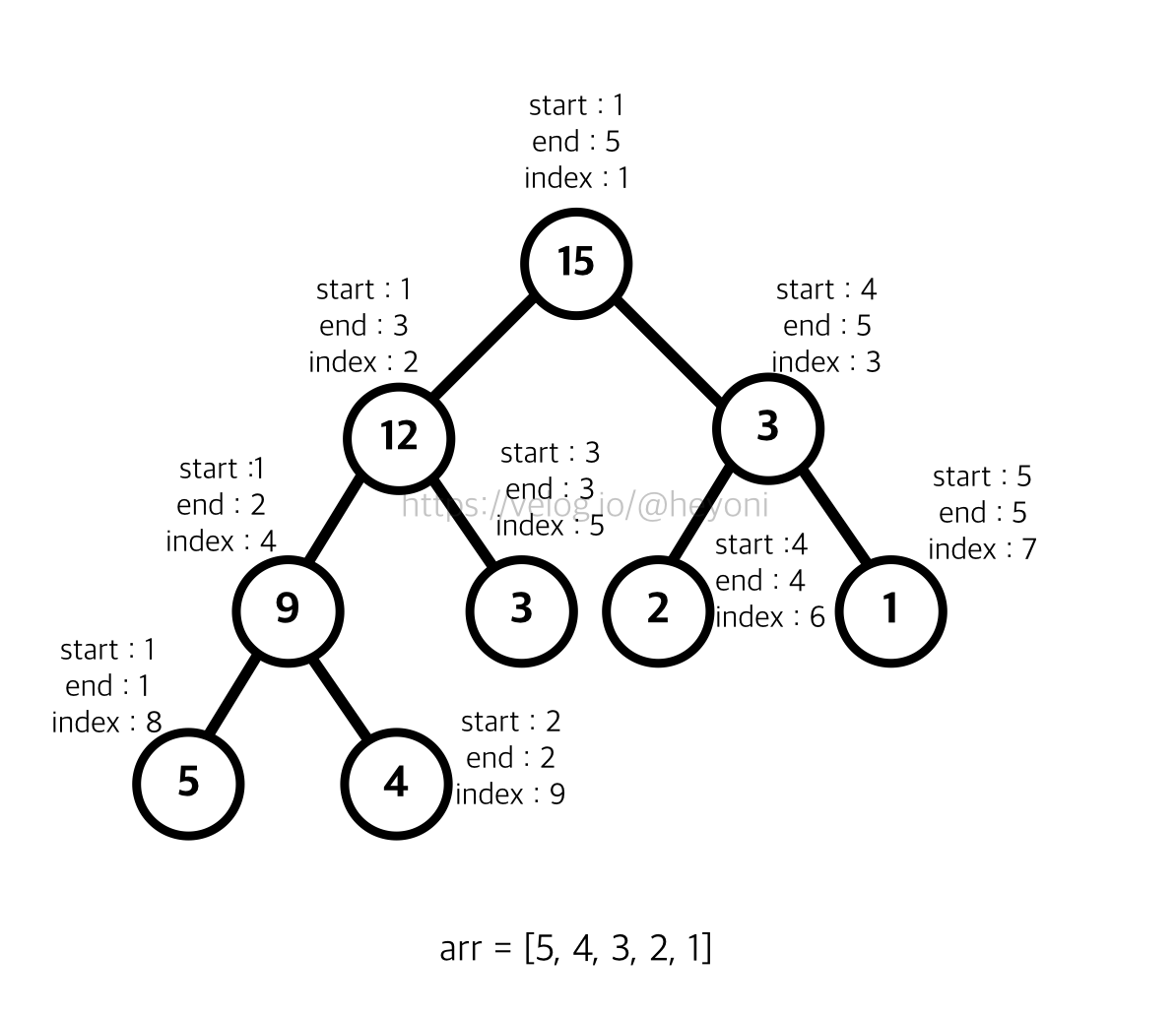
index가 1인 노드는 1부터 5까지 더한 27이라는 값을 노드에 담고있고,
index가 2인 노드는 1부터 3까지 더한 12라는 값을 노드에 담고있다.
같은 방법으로 트리를 그려볼 수 있을 것이다.

글로 잘 이해가 가지 않는다면 반드시 손으로 그려 볼 것!

그럼 이 트리를 어떻게 프로그램으로 구현할 수 있냐면,
위에서 말했던 index 값을 토대로 리스트에 저장하면 된다!
매우 간단하쥬?

즉, 위 트리는
리스트[0, 27, 12, 3, 9, 3, 2, 1, 5, 4] 표현할 수 있다.
(맨 앞에 0은 직관적으로 보기 위한 의미없는 수 입니다.)

1. 트리 만들기

그럼 이 트리를 직접 구현해보고 리스트에 넣는 코드를 짜보자.
이 트리를 만들기 전 가장 중요한 개념은

1. 현재 노드는 왼쪽 아래 노드와 오른쪽 아래 노드를 더한 값이다.
2. start와 end가 같아지는 때는 리프노드, 즉 맨 아래 노드라는 뜻이다.
3. 위 개념을 가지고 재귀함수를 만들 수 있다.

# 1. 트리 만들기
def init(start, end, index):
	# start와 end가 같다면 리프노드이다.
    if start == end:
        segment_tree[index] = l[start-1]
        return segment_tree[index]
	
    # 현재 노드는 왼쪽 아래 노드와 오른쪽 아래 노드를 더한 값이다.
    mid = (start+end) // 2
    segment_tree[index] = init(start, mid, index*2) + init(mid+1, end, index*2+1)
    return segment_tree[index]

위 코드가 이해가 안된다면 반드시 손으로 그려보세요.

2. 트리에서 값 찾기

트리를 구현해주었으면 이제 우리가 원하는 값인 부분합을 찾아줘야 한다.
마찬가지로 재귀함수로 구현해볼 수 있다.
아까 트리를 만들면서 1. 현재 노드는 왼쪽 아래 노드와 오른쪽 아래 노드를 더한 값이다.라는 것을 이해했을 것이다.
찾는 것도 마찬가지로 위 개념을 이용해서 구현하면 된다.

# 2. 트리에서 값 찾기
def find(start, end, index, left, right):
	# 찾으려는 범위가 start~end 범위보다 클 경우
    if start > right or end < left:
        return 0
        
    # 찾으려는 범위가 segment tree 노드안에 구현되어 있을 경우
    if start >= left and end <= right:
        return segment_tree[index]

	# 코드를 동작시키기 위한 기본 코드
    # 현재 노드는 왼쪽아래 + 오른쪽아래 노드이다.
    mid = (start + end) // 2
    sub_sum = find(start, mid, index*2, left, right) + find(mid+1, end, index*2+1, left, right)
    return sub_sum

3. 값 바꿔주기

값을 바꿔주는 것도 어렵지 않다.
다만 주의해야 할 점이, 값을 바꿔주는 것은 바꿔줄 값의 노드가 관여하고 있는 모든 값들을 찾으면서 바꿔줘야 한다.
그림을 다시 보자.

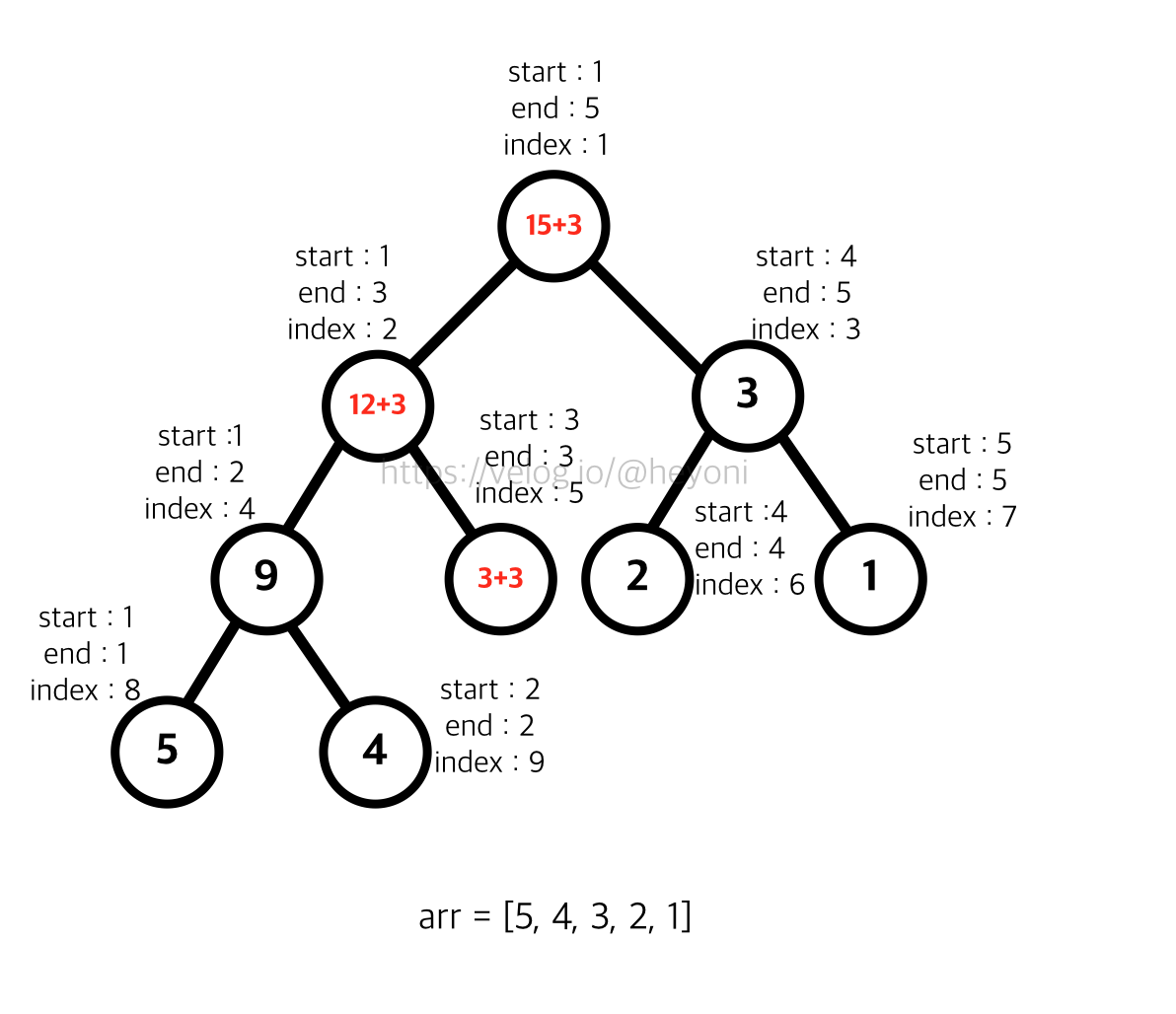
나는 3이라는 리프노드를 6으로 바꿔주고 싶지만, 현재 노드와 관련된 부모 노드들도 변환해주어야 한다.
이 점을 유념하며 구현하도록 하자.

def update(start, end, index, update_idx, update_data):
	# update 하려는 범위가 초과될 경우
    if start > update_idx or end < update_idx:
        return
    
    segment_tree[index] += update_data
	
    # 리프노드까지 바꿔주었으면 재귀함수를 끝낸다.
    if start == end:
        return

	# 내가 관여하고 있는 노드들을 찾아서 바꿔준다 -> 재귀함수로 구현
    mid = (start + end) // 2
    update(start, mid, index*2, update_idx, update_data)
    update(mid+1, end, index*2+1, update_idx, update_data)

이렇게 되면 모든 기능들은 구현이 된 것이다.

4. 제출 코드

마지막으로 제출 코드를 첨부하겠다.

# 0. 입력받기
import sys
input = sys.stdin.readline
from math import ceil, log

N, M, K = map(int,input().split())

l = []
segment_tree = [0]*(N*4)


# 1. 트리 만들기
def init(start, end, index):
	# start와 end가 같다면 리프노드이다.
    if start == end:
        segment_tree[index] = l[start-1]
        return segment_tree[index]
	
    # 현재 노드는 왼쪽 아래 노드와 오른쪽 아래 노드를 더한 값이다.
    mid = (start+end) // 2
    segment_tree[index] = init(start, mid, index*2) + init(mid+1, end, index*2+1)
    return segment_tree[index]

       
# 2. 트리에서 값 찾기
def find(start, end, index, left, right):
	# 찾으려는 범위가 start~end 범위보다 클 경우
    if start > right or end < left:
        return 0
        
    # 찾으려는 범위가 segment tree 노드안에 구현되어 있을 경우
    if start >= left and end <= right:
        return segment_tree[index]

	# 코드를 동작시키기 위한 기본 코드
    # 현재 노드는 왼쪽아래 + 오른쪽아래 노드이다.
    mid = (start + end) // 2
    sub_sum = find(start, mid, index*2, left, right) + find(mid+1, end, index*2+1, left, right)
    return sub_sum


# 3. 트리 값 바꿔주기
def update(start, end, index, update_idx, update_data):
	# update 하려는 범위가 초과될 경우
    if start > update_idx or end < update_idx:
        return
    
    segment_tree[index] += update_data
	
    # 리프노드까지 바꿔주었으면 재귀함수를 끝낸다.
    if start == end:
        return

	# 내가 관여하고 있는 노드들을 찾아서 바꿔준다 -> 재귀함수로 구현
    mid = (start + end) // 2
    update(start, mid, index*2, update_idx, update_data)
    update(mid+1, end, index*2+1, update_idx, update_data)


for _ in range(N):
    l.append(int(input()))

init(1, N, 1)

for _ in range(M+K):
    a, b, c = map(int,input().split())
    if a == 1:
        temp = c - l[b-1]
        l[b-1] = c
        update(1, N, 1, b, temp)

    elif a == 2:
        print(find(1, N, 1, b, c))

혹시나 설명이 잘못된 부분이 있으면 댓글 부탁드립니다.