MSC #3

dohoon·2021년 2월 24일

백준 그룹 : 빡알수 풀이

목록 보기

3/8

tistory에서 작성한 글을 옮겨왔습니다.

후기

MSC는 기본적인 문제들을 빠른 시간 내에 풀어내는 것이 목적입니다. 하지만 오늘 같은 경우, 문제의 난이도가 약간 높은 느낌이 없지 않았습니다.

그래서, 제일 먼저 거르고 보는 영어 문제를 넣는 것이 문제 선택의 폭을 줄이는 결과를 초래한다는 생각에 앞으로는 한글 문제만을 다루기로 했습니다.

그리고 junse1님이 브론즈의 개수를 2개로 늘리는 것이 좋겠다는 의견을 제시해 주셔서 반영하기로 했습니다.

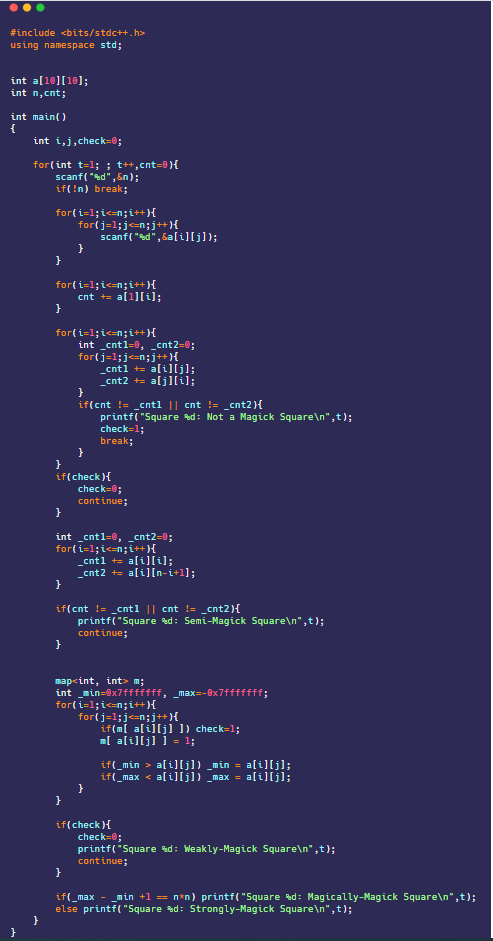
Ⓐ Magickology (2189)

by mc_ progw12

이 문제는 영어 문제입니다.

문제를 번역하는 데에 어려움이 있을 수 있었고, 또한 구현이 간단하지만은 않아서 많이 손절당한 문제입니다.

문제 번역

n*n의 격자 상태의 수 판을 받아서 다음 중 어떤 사각형인지 판별해라.

Not Magick : 각각의 행/열의 수들의 합들이 모두 같지는 않다.
Semi-Magick Square : 각각의 행/열의 수들의 합들이 모두 같지만, 두 대각선 위의 수들의 합들까지는 같지 않다.
Weakly-Magick Square : 각각의 행/열/대각선의 수들의 합이 모두 같다.
Strongly-Magick Square : Weakly-Magick Square 중 모든 수가 다 다른 사각형이다.
Magically-Magick Square : Strongly-Magick Square 중 차이가 1씩 나는 수열로 바꿔 쓸 수 있는 사각형. (사각형의 모든 수를 오름차순 정렬했을 때 인접한 두 수의 차이가 항상 1인 사각형)

문제 풀이

지문만 읽어봐도 구현이 미친 문제라는 것을 알 수 있습니다.

먼저, 보다 간단한 구현을 위해 대표로 1행의 모든 수들의 합을 구해 cnt에 저장해줍니다.
그런 다음, 각각의 가로, 세로줄의 수들의 합을 구합니다. (보다 간단한 구현을 위해 i번째 행과 j번째 열을 동시에 탐색했습니다.)
탐색을 하다가 합이 cnt와 다른 줄이 하나라도 나오면 not ~ 을 출력하고 탐색을 종료합니다.

여기서 탐색이 종료 되지 않았다면, 두 대각선도 탐색하고 탐색 종료 여부를 판단합니다.
만일 아직도 탐색이 끝나지 않았다면, 맵을 만들며 탐색을 시작합니다. (입력되는 정수의 범위를 모르기에..)

탐색을 하면서, 맵의 a[i][j]번 인덱스에 1을 대입하며 a[i][j]가 등장하였음을 체크해줍니다.
중간에 a[i][j]가 중복해서 나왔음이 확인되었다면 탐색을 마친 후 weakly를 출력해줍니다.
또한, 탐색 중에 계속하여 a[i][j] 값들의 min값, max값을 경신해 줍니다.

이렇게 하는 이유는, '모든 값이 다른가?'를 쉽게 구하려고 하기 때문입니다.

만일, '겹치는 수가 없고(겹치는 수가 있었다면 if(check)에서 걸려서 weakly를 출력하고 빠져나갔을 것입니다.) max값과 min값이 차이에서 1을 더한 것이 n*n과 같나?' 라는 말이 Strongly Square의 조건과 같기 때문에 그렇게 하였습니다.

맞은 사람이 필자 포함 11명인 기적인 문제

Ⓑ 타일 채우기 (2133)

by hgmhc

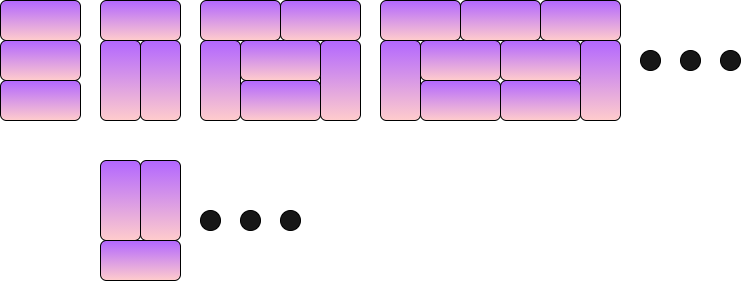
만들 수 있는 모든 모양들
타일 채우기 문제는 DP의 대표적인 유형입니다.

아니, 고등학교 점화식 단원에서도 제일 대표적이었죠. (지금은 빠졌지만...)

문제 풀이

문제 지문은 너무나도 직관적이기 때문에 굳이 풀어쓰지 않겠습니다.
이 문제의 포인트는 이겁니다.

직사각형으로 정형화된 형태를 다루는 것이 아니라면,
점화식을 세우는 것이 매우 까다로워진다는 것..!

(물론 적당히 복잡한 형태에 대해서 점화식 3개를 만든 후 합치는 방법도 있지만, 밑에 소개할 방법을 적용하는 것이 가능할 때에는 밑의 방법을 이용하는 것이 더 쉽습니다.)

그래서 타일들로 조합할 수 있는 모든 모양들을 나열해 봅시다.
위의 그림과 같이요.
패턴이 확고하게 보입니다, 그쵸?

그럼 이를 바탕으로 점화식을 세워봅시다.
$dp_n = dp_{n-2}+2\times (dp_{n-2}+dp_{n-4}+dp_{n-6}+\cdots)$

이것은 이해가 안 된다면 댓글로 남겨주세요. (그룹 회원은 DM 남겨주세요)

그런데 뒤에 꼬리가 길게 늘어지는 것을 볼 수 있죠?
그 부분을 없애지 않으면 $O(n^2)$ 시간 동안 공들여서 일일이 다 더해야 할 것입니다.

그래서 점화식을 세울 때 자주 사용하는 기법인,
이른바 꼬리 자르기 기법을 이용하도록 하겠습니다.

$\;\;\;[dp_n = dp_{n-2}+2\times (dp_{n-2}+dp_{n-4}+dp_{n-6}+\cdots)]$

$-[dp_{n-2} = dp_{n-4}+2\times (dp_{n-4}+dp_{n-6}+dp_{n-8}+\cdots)]$

$\;\;\;[dp_n-dp_{n-2} = dp_{n-2}-dp_{n-4}+2\cdot dp_{n-2}]$

꼬리가 잘려나갔죠?

그럼 이제 이항해서 정리해봅시다.

$dp_n = 4\cdot dp_{n-2}-dp_{n-4}$

이제 다 끝났습니다.
초항만 설정해주면 됩니다.

$n$ 이 3일 때까지만 설정하면 됩니다.

$dp_0 = 1, \; dp_1 = 0, \; dp_2 = 3, \; dp_3 = 0$

이제 구현은 여러분의 몫입니다!
모범 코드를 올려볼까 고민했지만, 너무 완벽한 1차원 DP이기 때문에
올리는 것이 무의미하다고 판단됩니다.

-끄읕-

p.s. 일반항을 직접 계산했습니다. DP 보다도 더 빠른 속도를 냅니다.

$dp_n=\frac{(1-\sqrt{3})\cdot (2-\sqrt{3})^{\frac{n}{2}}+(1+\sqrt{3})\cdot (2+\sqrt{3})^{\frac{n}{2}}}{2\sqrt{3}}$

Ⓒ Breed Assignment (5841)

by mc_ progw12
이 문제 역시 영어 문제라 푼 사용자 수가 적은 문제입니다.

N이 15이므로 간단하게 백트래킹으로 해결합시다.

백트래킹을 할 때 '1을 탐색하고 1과 연결된 애들을 탐색하고..' 이러다 보면 그래프 이론이 되어버리기 때문에 그냥 한 소 씩 차례대로 모든 가능한 경우의 수를 따지면서 탐색을 하면 됩니다. 만일 모든 소들이 조건이 없더라도 나올 수 있는 최대 경우의 수는 $3^{15} (=14,348,907)$ 이므로 시간초과가 뜰 염려가 없습니다.

먼저 소의 관계를 배열에 표시해줍니다. ('같다' = 1, '다르다' = -1)

그다음, 소의 색깔을 1,2,3으로 생각하고 ch 배열을 만듭니다.

ch[i] == 1이라는 것은 'p번째 소는 색깔 i일 수 없다.' 라는 것을 의미합니다.

i번째 소는 1부터 i-1번째와의 관계만 신경 써서 i번째 소의 가능한 색깔을 ch 배열로 추려냅니다.

이때, 가능한 경우가 0일 수도 있습니다. 예를 들어, S 1 3, S 2 3으로 주어 질 때, 1과 2 모두 조건 없이 배열되어 색이 각각 2와 3으로 지정됐다고 칩시다. 그러면 다음 3번째 소는 색깔이 2인 첫 번째 소와도 같아야 되고, 색깔이 3인 두 번째 소와도 같아야 됩니다. 하지만 이 둘을 모두 충족하는 색깔은 없으므로 경우의 수는 0이 됩니다.

이제 마지막 처리를 합니다.

for문을 돌면서, !ch[i] (= p번째 소가 색깔 i 인 경우가 가능하다.) 라면 소의 색깔을 i로 표시해주고, f(p+1)을 호출합니다. 함수 호출 후에는 다시 소의 색깔을 0 (= 없음) 으로 되돌려 줍니다.

Ⓓ 뒤집힌 덧셈 (1357)

by junse1
이 문제의 경우에는 char로 받고, 그걸 뒤집는 짓을 하거나, int로 받고 10으로 나누고,나머지를 저장한뒤에 그것을 수로 만들어서 더하는 방법도 있습니다. 그러나,string을 쓰면 한방에 풀립니다. reverse를 쓰면 string을 뒤집을 수 있는데,이것을 이용하면 빠르게 코드를 짤 수 있습니다.
코드는 밑에

문자열 함수를 애용합시다

Ⓔ 골드바흐의 추측 (9020)

by hgmhc
저는 급하게 풀다보니 이 문제를 두 포인터 기법을 이용하는 문제로 착각했습니다.
하지만, 합을 이루는 두 소수는 $n/2$ 를 기준으로 정확히 대칭을 이루기에
두 포인터와 시간 복잡도가 동일하면서도 더 짧은 구현이 가능해집니다.

일단, 에라토스테네스의 체를 이용하여 소수를 미리 모두 구해두어야 합니다.
그 후에 앞서 말한 방식으로 탐색을 진행하여 최초로 등장하는 두 쌍을 출력하면 됩니다.