TBC #2

tistory에서 옮겨왔습니다

후기

오늘은 새로운 admin 2명에게 문제 출제를 맡겼습니다.
오늘은 E번을 1번이라도 확인 해보았다면, 풀 수 있는 문제가 존재했습니다.
만약, E를 풀지 못하셨다면... 공부가 더 필요하다는 뜻입니다...

Ⓐ 쇠막대기 (10799)

by hgmhc

정확한 구현이 중요해요.

이 문제에서 틀릴 수 있는 포인트는 1가지인 것 같습니다.

')'로 닫으면서 내려가는 순간에도 하나의 막대기가 마무리 되어서 별개로 생각을 해야되는데, 그렇지 못하는 경우 말입니다.

일반적으로는 레이저를 쏘는 부분에서만 막대기의 개수를 증가시킬 것이라고 생각을 하기 때문이죠.

-끄읕-

Ⓑ 스택 수열 (1874)

by hgmhc

문제 이해가 안 되서 고생했습니다.

문제 이해

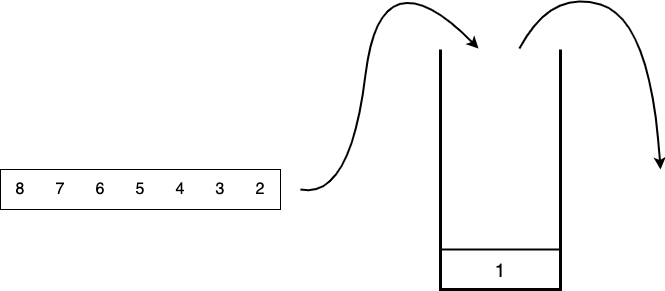
다음과 같은 방식으로 스택에 수를 넣고 빼는 시행을 반복하여
주어진 '스택 수열'을 만드는 것이 목표입니다.

이걸 이해했다면 구현은 상당히 쉽습니다.

구현

미리 배열 arr에 오름차순 형태로 값들을 저장한 뒤,
하나씩 스택 s에 넣어줍니다.

만약에 스택 s에서 지금 필요한 '스택 수열'의 원소가 등장한다면,
while문을 통해 '스택 수열'의 원소가 없을 때까지 뽑아줍니다.

그리고서 다시 스택에 값을 저장하는 과정을 거쳐줍니다.

Ⓒ 3으로 나누어 떨어지지 않는 배열 (2938)

by hgmhc
간단한 수학적 관찰이 필요한 문제입니다.
모든 입력을 3에 대한 나머지로서 관찰해봅시다.

$(x,y)$를 인접한 두 쌍이라 생각합시다. 순서는 고려하지 않습니다.

모두 적었습니다.

각각 나머지별로 집합 $A, B, C$라고 합시다.

다음의 경우들로 나눠봅시다.

$i)\; |A|=|B|+|C|$
ex)$0_{1010102010201010201020}1$

$ii)\; |A|=|B|+|C|+1$
ex)$0_{1012010201020102010101}0$

$iii)\; |A|<|B|+|C|$
ex)$11_{010201010201010}222$

어떠신가요?
이해가 확 되죠?
사실 저도 못 풀었어요.

Ⓓ 사냥꾼 (8983)

by hgmhc

이번 셋에서 제일 어려운 문제였어요.

그만큼 또 중요하기도 했습니다.
이 문제는 관점을 바꾸는 전략을 사용해야 합니다.

이 전략은 PS를 차치하고서라도,
논리적인 모든 활동에서 자주 쓰이지요.

무슨 말인고 하니, 사대를 기준으로 동물들을 잡는 것이 아니라 동물들을 기준으로 사대에 잡히는 가를 생각하자는 것입니다.

왜 그럴까요?

문제 풀이

기하적인 문제에서 공통적인 통찰이 하나 있습니다.

평면은 무지막지하게 넓기 때문에 좌표 하나하나를 따지는 류의 방식으로 풀 수 있는 문제는 극히 드뭅니다.
따라서 관찰해야 하는 점들에 대해서만 작업을 수행합니다.

이런 이유로 인해, 사대를 기준으로 일일이 범위 내에 동물이 있는가를 따지는 방법은 제일 먼저 배제하게 됩니다.

그럼 다음으로 떠오르는 아이디어는 사대를 기준으로 모든 동물들을 확인하는 것입니다.

이 과정은 시간이 너무 오래 걸립니다.
그렇다면, 동물들의 좌표를 정렬해서 생각해보면 시간을 줄 것 같네요.

하지만!
저 생각을 하셨다면 구현이 매우 더러워질 것이다라는 생각을 쉽게 하실 수 있습니다.

이 때, 관점을 바꿔주어야 합니다.
아! 동물을 기준으로 사대를 판단하자!
이 상태로 이진 탐색을 이용한다면 빠르게 결과를 도출할 수도 있겠다!

그럼 이제 구현을 해봅시다.

구현

$p$가 각 사대의 위치를 나타냅니다.

동물의 관점에서 사대를 보기로 했으니,
동물의 좌표는 배열에 저장하지 않아도 됩니다.

매 반복마다 동물의 좌표에 대해 사대들을 살펴보면 되기 때문이죠.

그 다음은 이진 탐색입니다.
$y \leq l$만 만족한다면 그 동물은 잡힐 가능성이 존재하게 됩니다.

그들에 대해서만 탐색을 진행하면 됩니다. (그리고 그렇지 않은 경우를 배제하지 않는다면 이상한 상황이 발생하므로 주의하세요.)

$x-(l-y)\leq p_k \leq x+(l-y)$인 자리를 찾아줍니다.

설명이 약간 허술한 느낌은 있지만 어느 부분을 보강해야 할지 잘 모르겠네요...
그러니 댓글로 질문 남겨주세요. (DM이 더 빨라요)

Ⓔ 큐 (10845)

by hgmhc

쉬운 문제가 너무 뒤에 나왔네요.
그래서 안 푸신 분들은 앞으로는 모든 문제를 한 번씩 읽어보시길 바랍니다.
만약, 못 푸셨다면 STL 공부를 다시 해주세요ㅠ