완전 탐색 알고리즘 중 하나인 DFS/BFS는 그래프를 탐색하는데 사용하는 알고리즘이다.

DFS/BFS 문제를 풀 때는 이 알고리즘을 직접 구현하고 상황에 맞게 수정하는 과정이 핵심적인 부분이지만, 실제 문제를 풀기 위해서는 입력받는 값들을 프로그램 상에 저장하는 전처리 과정이 필요하다.

이번 글에서는 입력된 그래프를 프로그램 상으로 저장하는 방법을 알아보고자 한다.

*이 글은 DFS/BFS를 공부한다면 먼저 풀어볼 백준 1260번의 입력 값을 기준으로 작성되었다.

백준 1260번 DFS와 BFS

그래프

우선 그래프에 대한 이해가 필요하다.

컴퓨터 상에서 그래프는 vertex(정점) 과 edge(간선)으로 이루어진 자료구조를 말한다.

그림으로 봤을 때 원 부분이 vertex(정점), 선 부분이 edge(간선)이고, 이를 입력 받을 때에는 정점 사이의 연결 관계(간선의 유무 여부)를 입력받는다.

그림의 1번 정점과 연결되어 있는 정점은 2번, 5번 정점으로 이를 입력 받을 때는, 띄어쓰기를 기준으로

1 2
1 5

라고 입력받게 되는 것이다. 이는 백준 1260번의 입력 예시에 잘 나와 있다.

(위의 그래프와 백준 1260번의 예제를 토대로 그린 그래프는 다르다. 단지 입력 형식이 같다는 뜻이다.)

또한 그림은 간선의 방향이 없는 무방향 그래프이므로
1 2
2 1
이 동일 표현임을 알 수 있다.

인접행렬과 인접 리스트

그래프의 대한 이해와 입력 형식에 대한 이해를 마쳤으니, 그래프를 저장하는 방식에 대해 알아보고자 한다.

그래프를 저장하는 방식에는 여러 가지가 있지만, 이번 포스팅에서는 간단하게 연결 여부만 확인하는 인접 행렬과 인접 리스트 방식만 설명할 것이다.

인접 행렬

인접 행렬은 그래프 간의 연결 관계(간선의 존재여부)를 행렬로 표현한 것이다.
이번 포스팅에서는 간선의 개수가 아닌 간선의 존재 여부만을 확인하기로 했으므로, 0과 1만으로 값을 나타낸다.

간선이 존재하지 않으면(정점이 연결되어 있지 않다면) 0, 간선이 존재하면(정점이 서로 연결되어 있으면) 1로 표시한다.

다음 그래프를 행렬로 나타내면 다음과 같다.

• 정점의 개수가 6개이고, 모든 정점간의 연결 관계를 나타내야 하므로 6*6 행렬이 생성되었다.
• 왼쪽부터 차례대로 1,2,3,4,5,6 정점 순이고, 위쪽부터 차례대로 1,2,3,4,5,6 정점 순이다. A[1][2] 와 A[2][1]은 1번과 2번 정점 사이의 관계(간선의 존재 유무)를 나타내는 것이다. 그래프 상으로 1번과 2번은 연결되어 있으므로 값은 모두 1이다.
• 정점 1번과 정점 1번의 관계는 A[1][1] 하나만 존재한다. 자기자신끼리의 관계는 무조건 0으로 표시한다. A[2][2], A[3][3] 모두 0이다.

구현하기에 앞서

1) 이 코드는 백준 1260번의 입력값을 기준으로 작성되었다.
2) 시작 정점이 1인 경우 인덱스 값을 조정하지 않기 위해 주어진 정점의 개수보다 +1만큼 크기를 더해 생성하였다.

## n:정점의 개수
n = int(input())
## 행렬 생성
lst = [[0] * n for i in range(n)]
## 행렬 한줄 씩 출력
for i in range(n):
    print(lst[i])

위 코드를 실행하게 되면 n을 5로 입력 했을 때

[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]

모든 요소값을 0으로 초기화한 5*5 이중 리스트가 생성되게 된다. 크기에 딱 맞게 생성한 게 아니냐고 묻는다면 그게 맞다.
하지만 리스트의 인덱스 값은 0부터 시작하므로, 후에 DFS/BFS를 구현하거나 디버깅을 할 때 알아보기 불편하다는 단점이 생긴다.

이런 불편함을 최소화하기 위해 정점의 개수가 5라면 6*6행렬을 만들어주고 [1][1]인덱스부터 저장을 시켜주는 것이다.
[0][i],[i][0]은 0으로 초기화해주고 깡그리 무시한다.

예시
n=5일 때,
1 3을 입력받으면,(1번 정점과 3번 정점이 서로 연결되어 있다.)

정점에 딱 맞게 초기화 했을 때,
[0, 0, 1, 0, 0]
[0, 0, 0, 0, 0]
[1, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]

봤을 땐 편하지만, 정점 1과 정점 3의 연결 여부를 확인하기 위해선 [0][2], [2][0] 값을 참조해야 한다.

정점 +1만큼 초기화 했을 때,
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]

정점 1과 정점 3의 연결 여부를 확인 할 때, 인덱스 값 그대로[1][3], [3][1]을 확인하면 되므로 참조할 때 훨씬 편하다.

구현

import sys
## n : 정점의 개수, m : 간선의 개수, v : 시작 정점
n,m,v= map(int, sys.stdin.readline().split())
## 그래프를 저장할 행렬 생성, 기본 값은 0으로
graph = [[0] * (n+1) for i in range(n+1)]
## 정점 연결 관계 입력(간선의 개수가 m이므로 정점간의 관계도 m개이다. 따라서 m번 반복한다.)
for i in range(m):
    x,y = map(int, sys.stdin.readline().split())
    ## 정점끼리 연결되어 있으면 1로 수정
    graph[x][y] = graph[y][x] = 1
## 행렬 출력
for i in range(m):
    print(graph[i])

인접 리스트

인접 리스트는 그래프에 연결된 정점들을 연결 리스트로 구현하는 방법이다. 파이썬은 리스트로 구현한다.

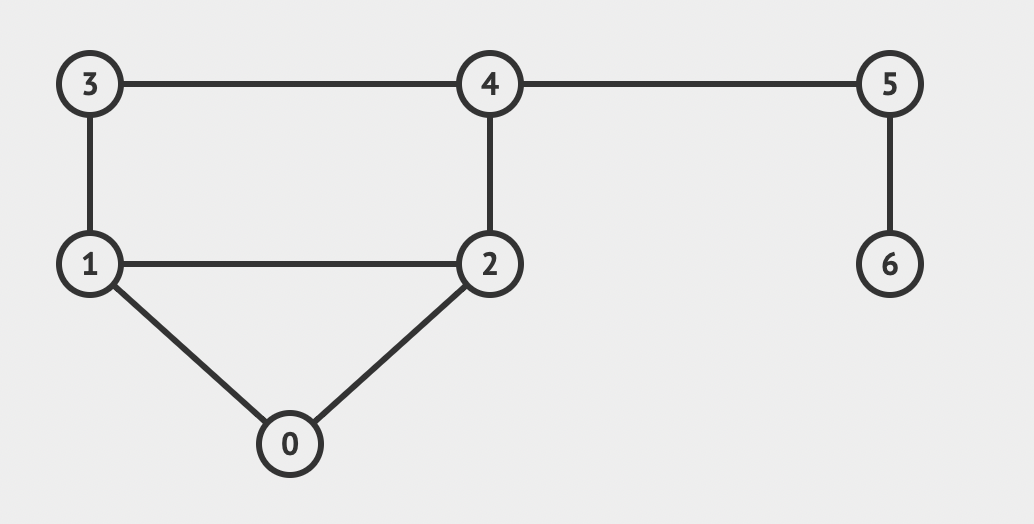
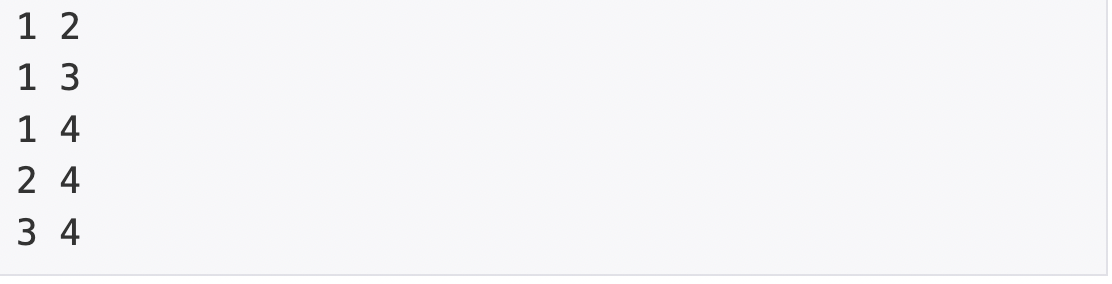
이런 그래프가 있다면, (이해를 돕기 위해 시작 정점이 0인 그래프를 가져왔다.)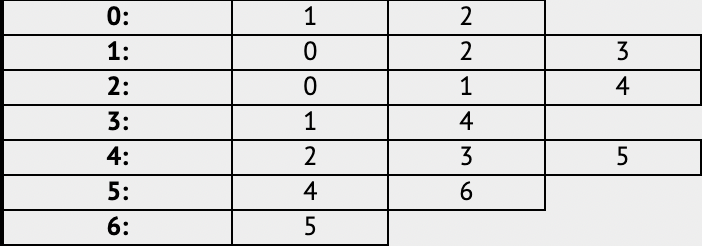

이런 식으로 저장이 되게 된다.
0:, 1:, 2: 부분을 정점의 번호라고 생각하면 된다. 정점의 번호는 인접 리스트의 인덱스 값으로 저장이 된다.

0번 정점에는 1번, 2번 정점이 연결되어 있으므로,
0번 인덱스에는 [1,2]가,
1번 정점에는 0번 2번 3번 정점이 연결되어 있으므로,
1번 인덱스에는 [0,1,2]가 저장이 된다.

구현

백준 1260번은 시작 정점이 1이므로 인덱스 값을 참조하기 쉽게, n+1만큼 생성하고 정점 값 그대로 참조한다.

## n : 정점의 개수, m : 간선의 개수 , v 시작 정점 번호
n,m,v = map(int, sys.stdin.readline().split())

## 인접 리스트 생성 
graph = [[] for i in range(n+1)]

## 정점간의 연결 관계 입력
for i in range(m):
    x,y = map(int, sys.stdin.readline().split())
    if x == y:
        graph[x].append(y)
    else:
        graph[x].append(y)
        graph[y].append(x)
## 정렬 후 출력        
for i in range(len(graph)):
    graph[i].sort()
    print(graph[i])

인접 행렬과 인접 리스트 비교

인접 행렬

• 구현이 비교적 쉽다.
• 두 정점 간의 인접 여부를 확인할 때, 인덱스 값만 참조하면 되므로 시간 복잡도가 O(1)이다. 후술할 인접 리스트보다 빠르다.
• 메모리를 많이 차지한다. 정점의 개수가 N개라면 이번 포스팅에서 구현한 방식으로는 O((N+1)^2)의 공간 복잡도가 든다.
• 정점에 비해 간선이 적으면(희소 그래프)이면 비효율적이다.

인접 리스트

• 구현이 비교적 어렵다.
• 두 정점 간의 인접 여부를 확인할 때 시간 복잡도는 최악의 경우 리스트를 모두 검색해야 하기 때문에 O(N)이다.
• 메모리를 덜 차지한다.