선형 회귀

• 선형 회귀: 하나 이상의 특성(설명변수, x)과 연속적인 타킷 변수(응답 변수, y) 사이의 관계를 모델링 하는 것.
  • 단순 회귀: 특성 한개
  • 다중 회귀: 특성 여러 개

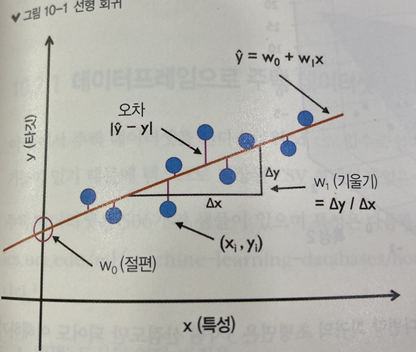
• 회귀직선: 위 그림처럼 데이터와 가장 잘 맞는 직선
• 오프셋(잔차,오차) : 이 회귀 직선과 훈련 샘플 사이의 직선 거리

탐색적 데이터 분석

이상치를 감지하고 데이터 분포를 시각화하거나 특성 간의 관계를 나타내는 데 도움

• 예) 산점도 행렬, 상관관계 행렬(공분산 행렬)

최소 제곱 선형 회귀 모델

: 훈련 샘플까지 수직거리의 제곱합(오차의 제곱합)을 최소화하여 가장 적합한 선형 모델(직선)을 찾는 방법

왜 제곱합일까?

• 그냥 합이면 0이 되버리는 문제 발생 -> 양수/음수 상쇄 문제를 해결하고,큰 오차에 민감하게 반응하기 위해서!

so, 회귀 모델이 오차에 큰 영향을 받는 것! > 이상치 처리 방법 고민!

RANSAC

이상치를 함부로 제거할 수는 없음
why? 해당 분야의 지식뿐만 아니라 데이터 과학자로서 식견도 필요하기 때문

이상치를 제거하는 방식 대신 RANSAC!!!!

• 이상치가 포함된 데이터에서, 데이터를 무작위로 샘플링하여 반복적으로 모델을 추정하고, 가장 많은 내부점을 가지는 모델을 선택하는 알고리즘
  => 이상치에 영향을 받지 않는 모델을 반복적 생성, 반복 샘플링 과정에서 이상치가 포함된 모델은 내부점 개수가 적기 때문에 자동으로 제거

[원리]
1. 랜덤 샘플링: 데이터에서 임의로 일부 샘플을 선택해 모델을 추정 (예: 직선 모델에 두 점 선택).
2. 잔차 계산: 나머지 데이터와 모델 간의 거리를 계산하고, 거리가 임계값 이하인 데이터를 내부점으로 간주.
3. 모델 평가: 내부점의 개수를 세어 모델을 평가하고, 가장 많은 내부점을 가진 모델을 최적 모델로 선택.
4. 반복: 위 과정을 여러 번 반복하여 이상치의 영향을 최소화한 최적 모델을 찾음 = 즉 내부점 개수가 많은!

회귀에 규제 적용

규제: 과대적합 문제를 방지 by 부가 정보 손실(ex. 일부 정보 무시)

• 규제 증가 -> 모델가중치값 감소

• 라쏘(L1규제)

  • 비용함수에 가중치의 절댓값 합을 추가한 모델
  • 일부 가중치를 0으로 만듦 -> 특성 선택 효과, 일부 특성의 가중치를 0으로 만들어 모델이 해당 특성을 완전히 무시하도록 만듦

• 릿지 회귀(L2규제)

  • 비용 함수에 가중치의 제곱합 추가한 모델
  • 가중치를 0에 가깝게 만들지만, 완전히 0으로는 X ->모델의 복잡도를 완화하면서 모든 특성을 활용. 또는 덜 중요한 특성의 정보가 약화

• 엘라스틱 넷

결정 트리 회귀

• 결정 트리 장점: 비선형 데이터를 다룰 때 특성 변환 불필요
• 가중치가 적용된 특성 조합을 고려하는 것이 아니라 한 번에 하나의 특성만 평가!(특성 값의 크기보다는 각 노드의 임계값을 기준으로 분할하는 방식에 의존하므로, 결정트리에서는 특성 정규화나 표준화가 필요X)

랜덤 포레스트 회귀

• 단일이 아닌 여러개의 결정트리를 사용하니 단일 결정 트리보다 더 나은 일반화 성능 나타남
• 왜? 무작위성이 모델의 분산을 낮추기 때문
• 장점: 이상치에 덜 민감하고 하이퍼파라미터 튜닝이 많이 필요X -> 유일한 하이퍼파라미터는 앙상블의 트리 개수