문제

---

11주차 아이템 줍기

풀이

알고리즘

---

먼저 이 문제는 구현과 BFS로 이루어진 문제이다.

1. 이 문제는 입력으로 받는 직사각형의 좌표, 캐릭터 좌표, 아이템 좌표를 모두 2배 해줌으로써 문제를 쉽게 풀어낼 수 있다.
   (이것만 알았다면 문제의 80%는 푼 거나 다름없다. 이유는 아래에서 설명하겠다.)

	characterX *= 2, characterY *= 2, itemX *= 2, itemY *= 2;

2. 각 직사각형들의 대각에 위치하는 좌표를 입력 받았으니, 배열을 통해서 표현해준다.
   필자는 직사각형을 1로 표현해주겠다.

    for (int i = 0; i < rectangle.size(); i++)
    {
    	// 입력으로 받은 직사각형의 좌표도 모두 2배로 늘린다
        for (int j = 0; j < rectangle[0].size(); j++)
            rectangle[i][j] = rectangle[i][j] * 2;
		
        x1 = rectangle[i][0], y1 = rectangle[i][1];
        x2 = rectangle[i][2], y2 = rectangle[i][3];

	// 직사각형의 시작좌표부터 대각에 있는 끝 좌표까지 모두 1을 입력해주었다.
        for (int y = y1; y <= y2; y++)
            for (int x = x1; x <= x2; x++)
                board[y][x] = 1;
    }

3. 각 직사각형들의 테두리만 BFS로 돌 것이므로 직사각형의 내부는 모두 0으로 채워준다.

    for (int i = 0; i < rectangle.size(); i++)
    {
        x1 = rectangle[i][0], y1 = rectangle[i][1];
        x2 = rectangle[i][2], y2 = rectangle[i][3];
	// 간단하게 시작 좌표 + 1 ~ 끝 좌표 - 1 까지 돌면 직사각형 내부만 돌 수 있다.
        for (int y = y1 + 1; y < y2; y++)
            for (int x = x1 + 1; x < x2; x++)
                board[y][x] = 0;
    }

4. BFS

    queue<pair<int, int>> q;
    q.emplace(characterY, characterX);
    while (!q.empty())
    {
        int y = q.front().first;
        int x = q.front().second;
        q.pop();

	// 아이템 좌표에 도달했으므로 탐색 종료
        if (y == itemY && x == itemX)
            break;

        for (int i = 0; i < 4; i++)
        {
            int nextY = y + dy[i];
            int nextX = x + dx[i];

            if (board[nextY][nextX] == 1)
            {
                q.emplace(nextY, nextX);
                // 다음 좌표 = 현재 좌표 + 1 로 얼마나 이동했는지 표시해준다.
                // 미로 탐색과 같은 이치
                board[nextY][nextX] = board[y][x] + 1;
            }
        }
    }

왜 좌표를 모두 2배로 늘려줘야 할까?

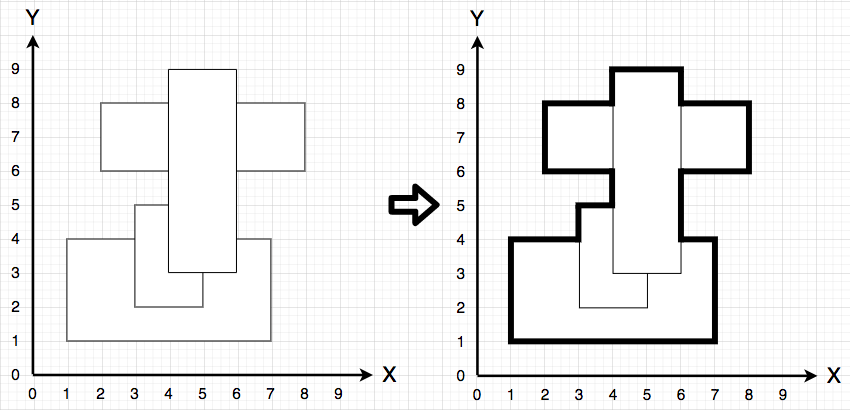
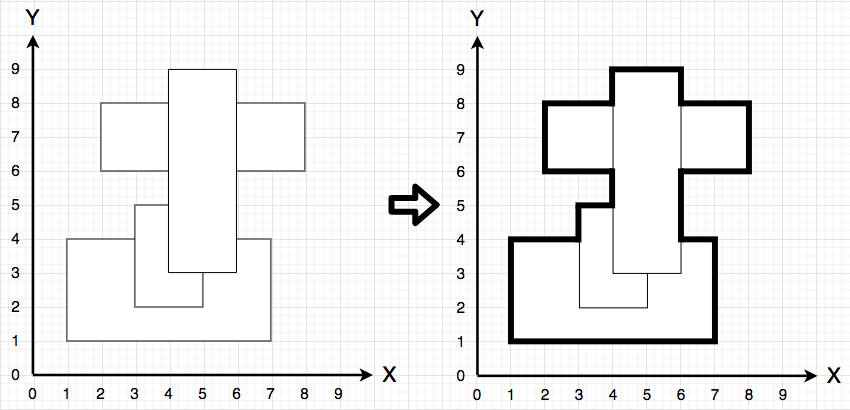
• 먼저 위의 그림을 보자.
  위 그림은 테스트 케이스 1번을 위의 알고리즘 3번까지 끝낸 모습이다.(상하가 반전되어 있다. 배열은 [0,0]이 위쪽인 것이 자연스러우므로)
  왼쪽은 좌표를 2배로 늘리지 않은 원본의 모습이라고 할 수 있고, 오른쪽은 좌표를 2배 늘려서 표현한 것이다.

• 이런 식으로 좌표를 2배 늘리는 것이 문제를 푸는 데에 무슨 도움을 주는지 직접 해보고 깨닫는다면 더 좋을 것이다.

• 마저 설명하자면, 좌표값을 배열에 그대로 표현하려다 보면 왼쪽 그림의 주황색 박스처럼 테두리가 겹쳐져 표현되는 경우가 생긴다.

• 그 상태로 왼쪽의 그림을 BFS로 탐색할 시에 두갈래 길을 만나게 되는 경우가 존재하게 된다.
  그렇다면 BFS는 아이템이 있는 좌표에 도달은 하겠지만, 두 갈래 길 중 최단 경로를 선택하여 우리에게 전달해줄 것이다.
  이는 곧 테두리를 정상적으로 돌지 않았다는 의미와 같다.

• 하지만 오른쪽과 같이 좌표를 처음부터 2배로 늘려주면 테두리가 겹치는 문제가 해결되고, 이는 곧 BFS가 두 갈래 길을 만나는 경우도 사라지게 됨을 의미한다.
  이런 식으로 좌표를 단순히 2배로 늘림으로써 문제를 쉽게 풀어낼 수 있는 것이다.

코드

---

#include <string>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;

// 동 서 남 북
int dy[] = {0, 0, 1, -1};
int dx[] = {1, -1, 0, 0};

int solution(vector<vector<int>> rectangle, int characterX, int characterY, int itemX, int itemY)
{
    int answer = 0;
    
    // 1. 캐릭터 좌표, 아이템 좌표 모두 2배로 늘린다.
    characterX *= 2, characterY *= 2, itemX *= 2, itemY *= 2;
    // board: 직사각형을 표현할 배열이다.(문제에 직사각형을 나타내는 모든 좌표값은 50이하라고 했지만, 
    // 우리는 모든 좌표값에 대해 2배를 할 것이므로 50*2=100이므로 좌표값은 최대 100이 될 것이다.)
    vector<vector<int>> board(110, vector<int>(110));
    
    // 직사각형의 시작점과 끝점
    int x1, y1, x2, y2;
    
    // 2. 직사각형을 board 배열에 모두 입력해준다.
    for (int i = 0; i < rectangle.size(); i++)
    {
        for (int j = 0; j < rectangle[0].size(); j++)
            rectangle[i][j] = rectangle[i][j] * 2;

        x1 = rectangle[i][0], y1 = rectangle[i][1];
        x2 = rectangle[i][2], y2 = rectangle[i][3];

        for (int y = y1; y <= y2; y++)
            for (int x = x1; x <= x2; x++)
                board[y][x] = 1;
    }

    // 3. 직사각형의 내부는 모두 0으로 채워준다.
    for (int i = 0; i < rectangle.size(); i++)
    {
        x1 = rectangle[i][0], y1 = rectangle[i][1];
        x2 = rectangle[i][2], y2 = rectangle[i][3];

        for (int y = y1 + 1; y < y2; y++)
            for (int x = x1 + 1; x < x2; x++)
                board[y][x] = 0;
    }

    // 4. BFS
    queue<pair<int, int>> q;
    q.emplace(characterY, characterX);
    while (!q.empty())
    {
        int y = q.front().first;
        int x = q.front().second;
        q.pop();

        if (y == itemY && x == itemX)
            break;

        for (int i = 0; i < 4; i++)
        {
            int nextY = y + dy[i];
            int nextX = x + dx[i];

            if (board[nextY][nextX] == 1)
            {
                q.emplace(nextY, nextX);
                board[nextY][nextX] = board[y][x] + 1;
            }
        }
    }

    // 좌표를 모두 2배로 늘려서 계산했으니 answer에는 2로 나눈 아이템의 좌표값을 넣어주면 정답이다.
    answer = board[itemY][itemX] / 2;
    return answer;
}

int main()
{
    vector<vector<int>> rectangle = {{1, 1, 7, 4}, {3, 2, 5, 5}, {4, 3, 6, 9}, {2, 6, 8, 8}};
    int characterX = 1;
    int characterY = 3;
    int itemX = 7;
    int itemY = 8;

    solution(rectangle, characterX, characterY, itemX, itemY);
}

여담

오래간만의 위클리 챌린지 레벨 3이었다. 안그래도 한 번 레벨 3이 나올 때가 된 거 같다는 생각은 하고 있었는데, 막상 나온 걸 보고서는 지레 겁먹고 오늘에서야 각잡고 풀었다.
사실 위의 '좌표를 2배로 늘린다'라는 아이디어만 생각해낼 수 있다면 레벨 2나 다름 없다.(물론 그게 어려워서 레벨3이겠지만)

그래도 생각보다 오래 걸리지는 않았고 3주차의 레벨 3문제보다는 훨씬 쉽다고 느껴졌다. 이 글을 읽는 여러분도 그렇게 느꼈을까?
어쩌면 그간 해왔던 노력 덕분에 이렇게 느끼는지도 모르겠다. 3주차 때와 비교해서는 알고리즘만 80문제 정도는 더 풀어봤으니까.

곧 졸업이 다가오면서 정말 하루도 빠지지 않고 공부와 취준으로 바쁘게 지내는데 오늘 넷마블 서류&코딩테스트를 합격했다.
그래도 해왔던 노력이 허투루 한 것은 아니었다는 느낌도 들고 오묘한 느낌이다.
다음주는 넷마블테스트를 보기 위해서 용산으로 긴 여정을 떠날 예정이다.
여러분들도 같이 화이팅 하셨으면 좋겠다!