
5.3 비선형 자료 구조
비선형 자료 구조란 일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조를 말한다. 일반적으로 트리나 그래프를 말한다.
5.3.1 그래프
그래프는 정점과 간선으로 이루어진 자료구조를 말한다.
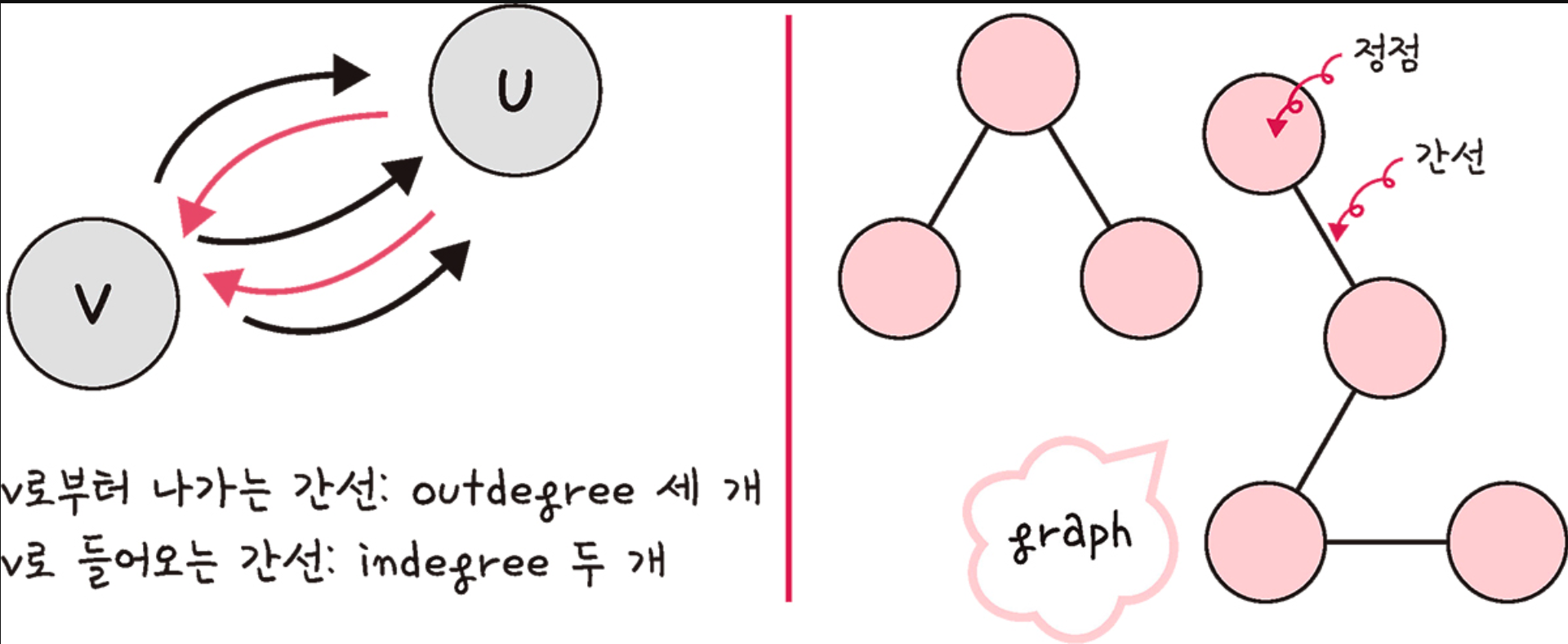
- 정점(Vertex): 그래프에서 하나의 개체를 나타내는 점으로 표현한다.
- 간선(Edge): 정점과 정점 사이를 연결하는 선으로 표현된다.
- 단방향 간선(Directed Edge): 방향성이 있는 간선이다.
- 양방향 간선(Undirected Edge): 방향성이 없는 간선이다.
- outdegree: 특정 정점에서 나가는 간선의 개수이다.
- indegree: 특정 정점으로 들어오는 간선의 개수이다.
가중치(Weight): 그래프의 간선에 부여된 값으로 해당 간선을 통해 이동하는 비용이나 거리를 나타낸다.
5.3.2 트리(Tree)
- 그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있다.
- 트리 구조로 배열된 일종의 계층적 데이터 집합이다.
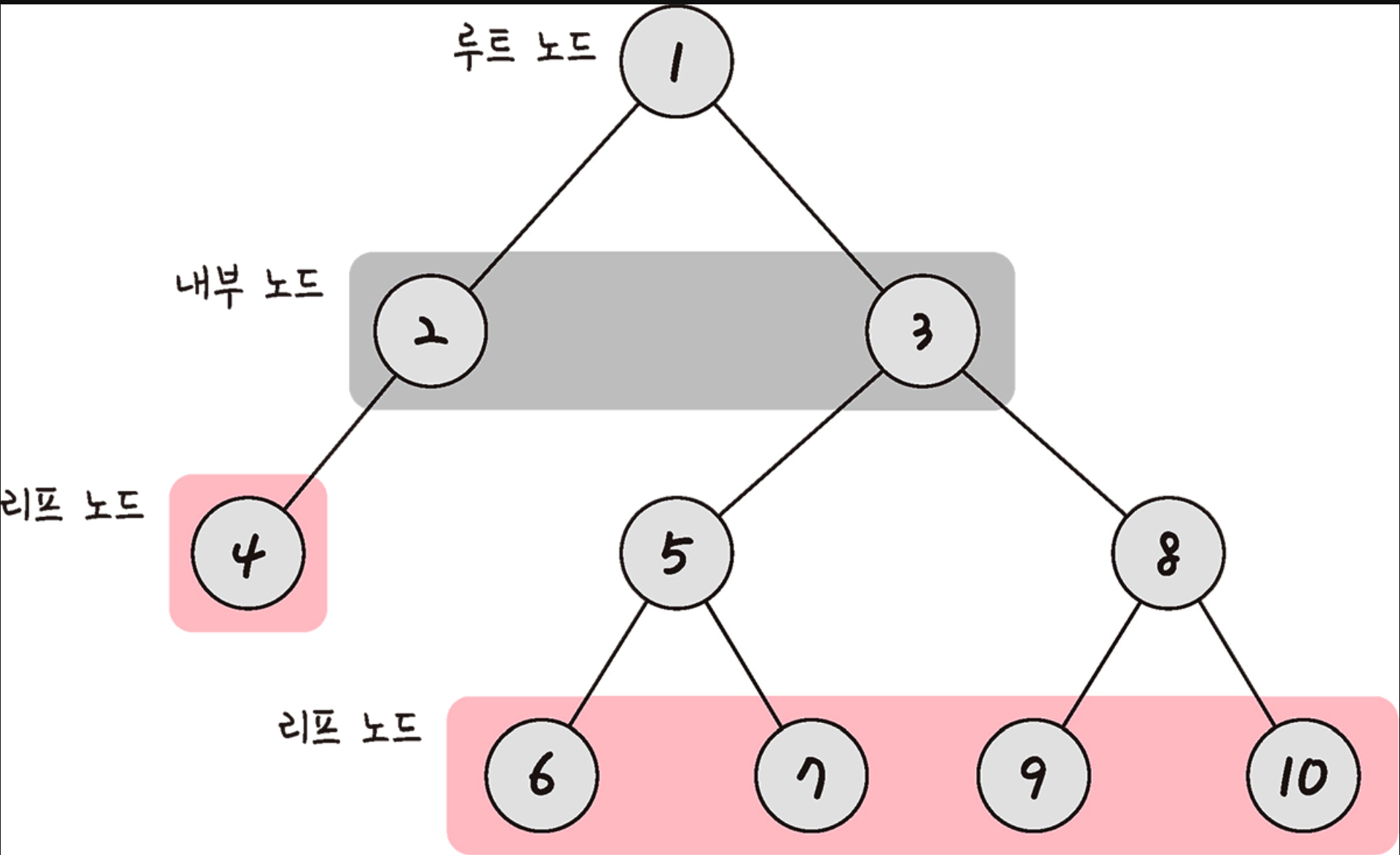
- 루트 노드, 내부 노드, 리프 노드 등으로 구성된다.
루트 노드(Root Node): 트리의 최상단에 위치해서 부모가 없는 노드
내부 노드(Internal Node): 루트 노드와 리프 노드 사이에 있는 노드
리프 노드(Leaf Node): 트리의 끝단에 위치해서 자식이 없는 노드
트리의 특징
트리는 그래프의 일종이며 다음 특징을 가진다는 점이 다르다.
- 부모, 자식 계층 구조를 가진다.
- 같은 경로 상에서 어떤 노드보다 위에 있으면 부모 노드, 아래에 있으며 자식 노드가 된다.
- 간선의 수 = 노드의 수 - 1 이다.
- 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 존재한다.
트리의 구성
트리는 루트 노드, 내부 노드, 리프 노드로 이루어져 있다.
루트 노드
가장 위에 있는 노드.
보통 트리 문제가 나오고 트리를 탐색할 때 루트 노드를 중심으로 탐색하면 문제가 쉽게 풀리는 경우가 많다.
내부 노드
루트 노드와 리프 노드 사이에 있는 노드.
리프 노드
리프 노드는 자식 노드가 없는 노드.
트리의 높이와 레벨
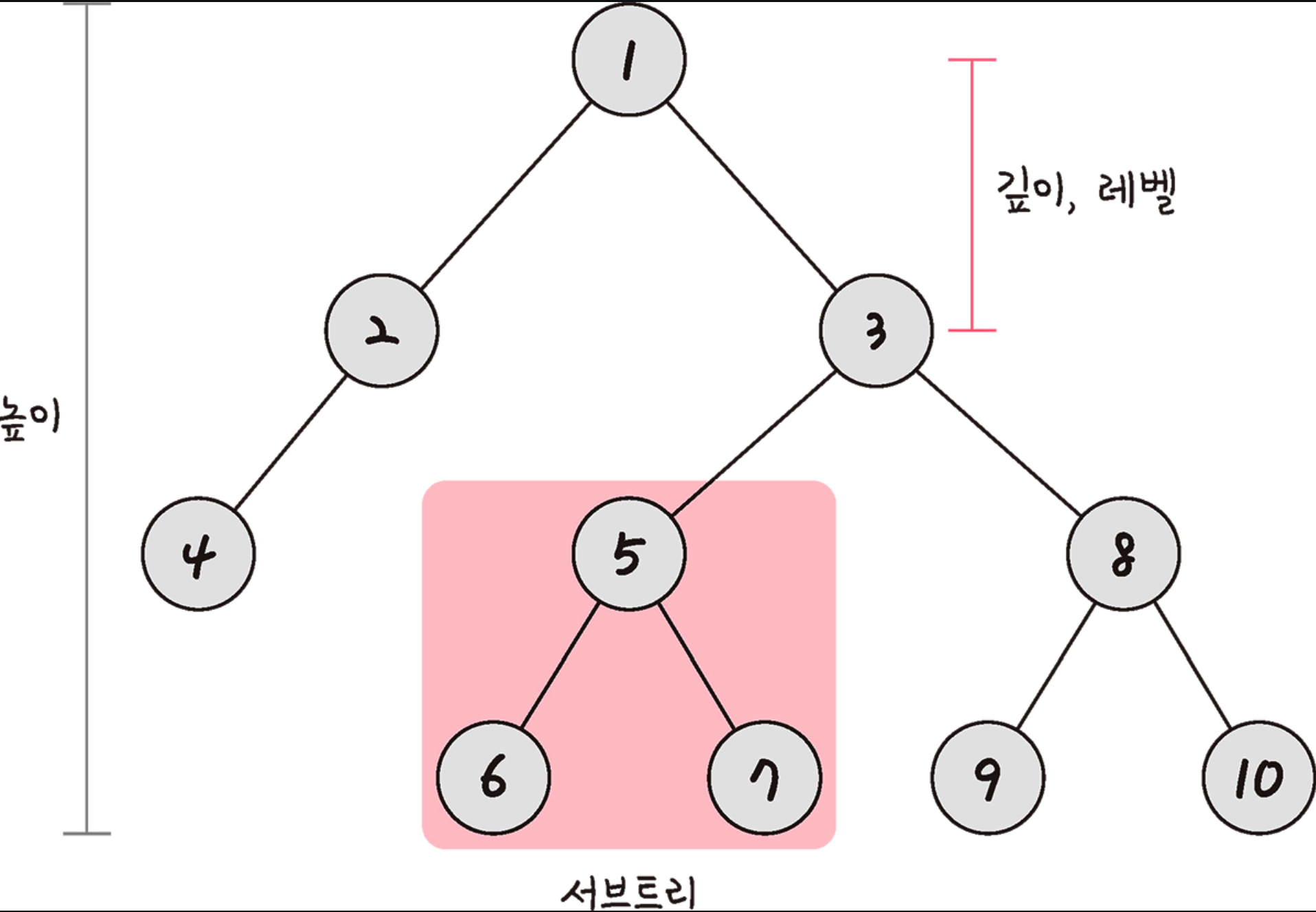
- 깊이(Depth): 루트 노드부터 특정 노드까지 최단 거리로 갔을 때의 거리이다.
- 높이(Height): 루트 노드로부터 리프 노드까지 거리 중 가장 긴 거리이다.
- 레벨(Level): 트리 계층 구조에서 각 층을 나타낸다. 보통 깊이와 같은 의미를 가진다.
- 서브트리(Subtree): 트리 내에 있는 부분집합을 의미한다.
이진 트리
이진 트리는 자식의 노드 수가 두 개 이하인 트리를 의미한다.
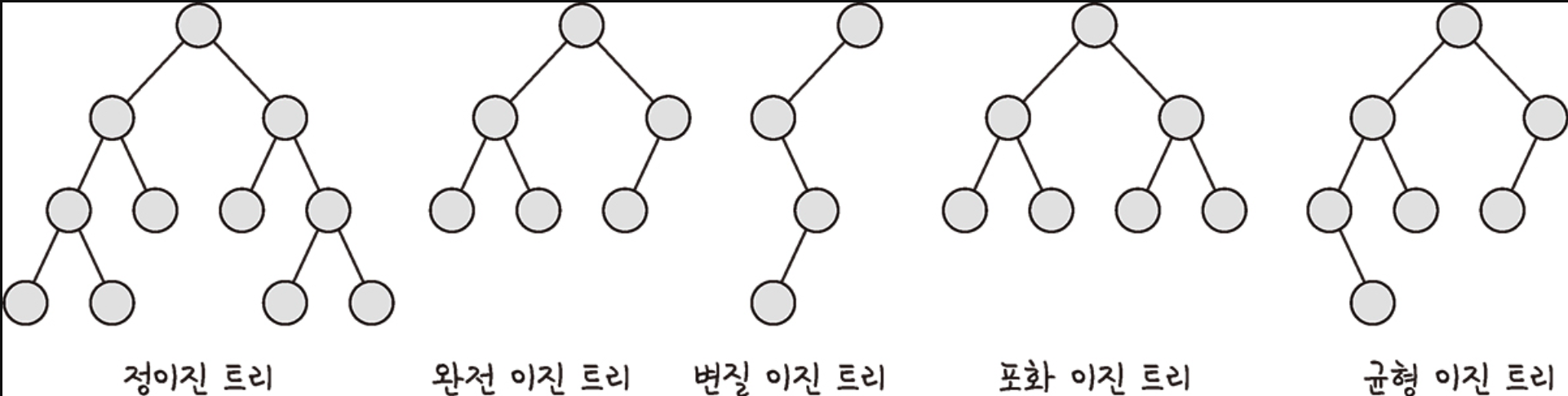
- 정이진 트리(full binary tree): 자식 노드가 0 또는 두 개인 이진 트리이다.
- 완전 이진 트리(complete binary tree): 왼쪽에서부터 채워져 있는 이진 트리이다.
- 변질 이진 트리(degenerate binary tree): 자식 노드가 하나밖에 없는 이진 트리이다.
- 포화 이진 트리(perfect binary tree): 모든 노드가 꽉 차 있는 이진 트리이다.
- 균형 이진 트리(balanced binary tree): 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리이다.
이진 탐색 트리
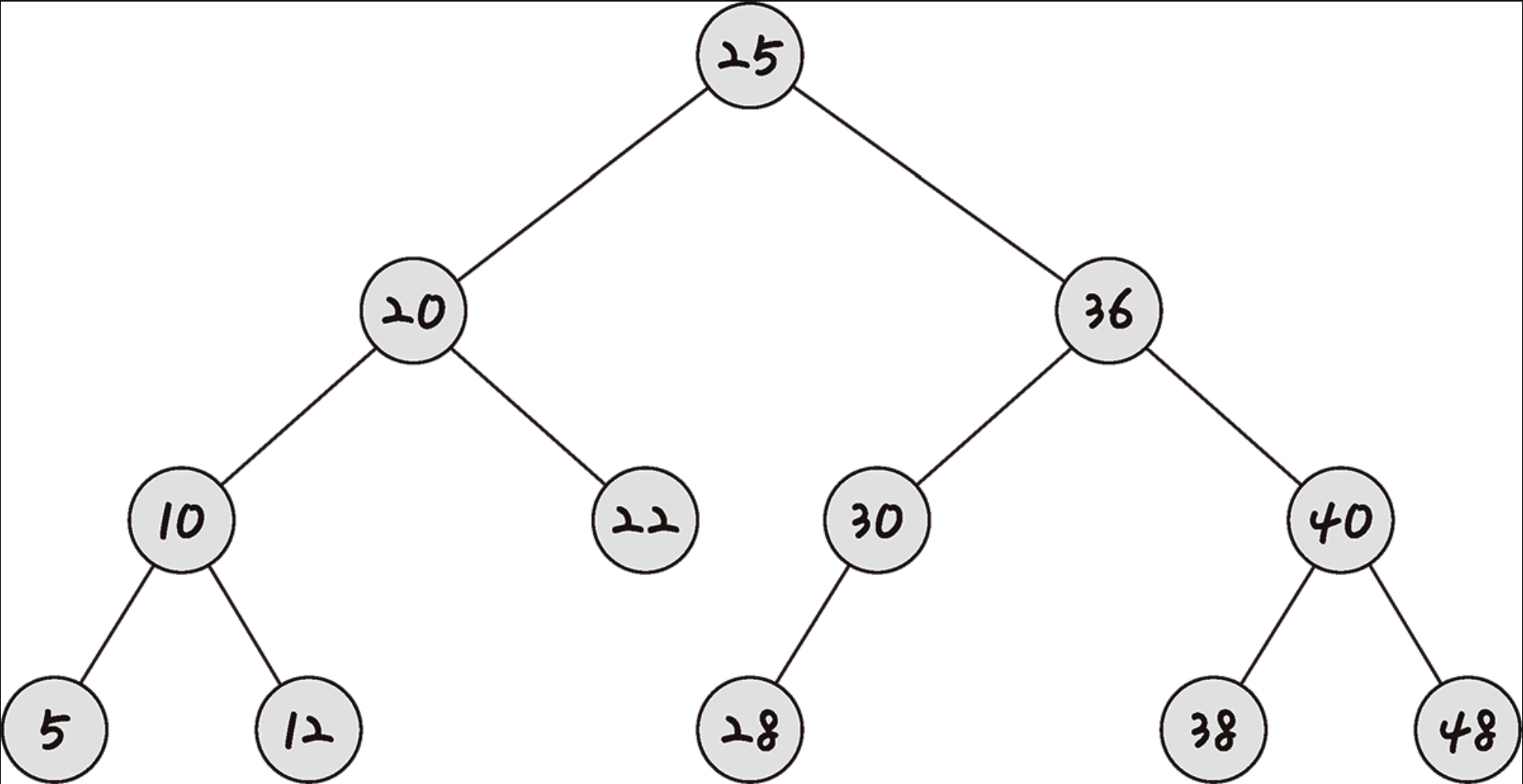
- 노드의 왼쪽 하위 트리에는 노드 값보다 작은 값이 있는 노드만 포함된다.
- 노드의 오른쪽 하위 트리에는 노드 값보다 큰 값이 있는 노드만 포함된다.
비선형적 이진 탐색 트리와 선형적 이진 탐색 트리
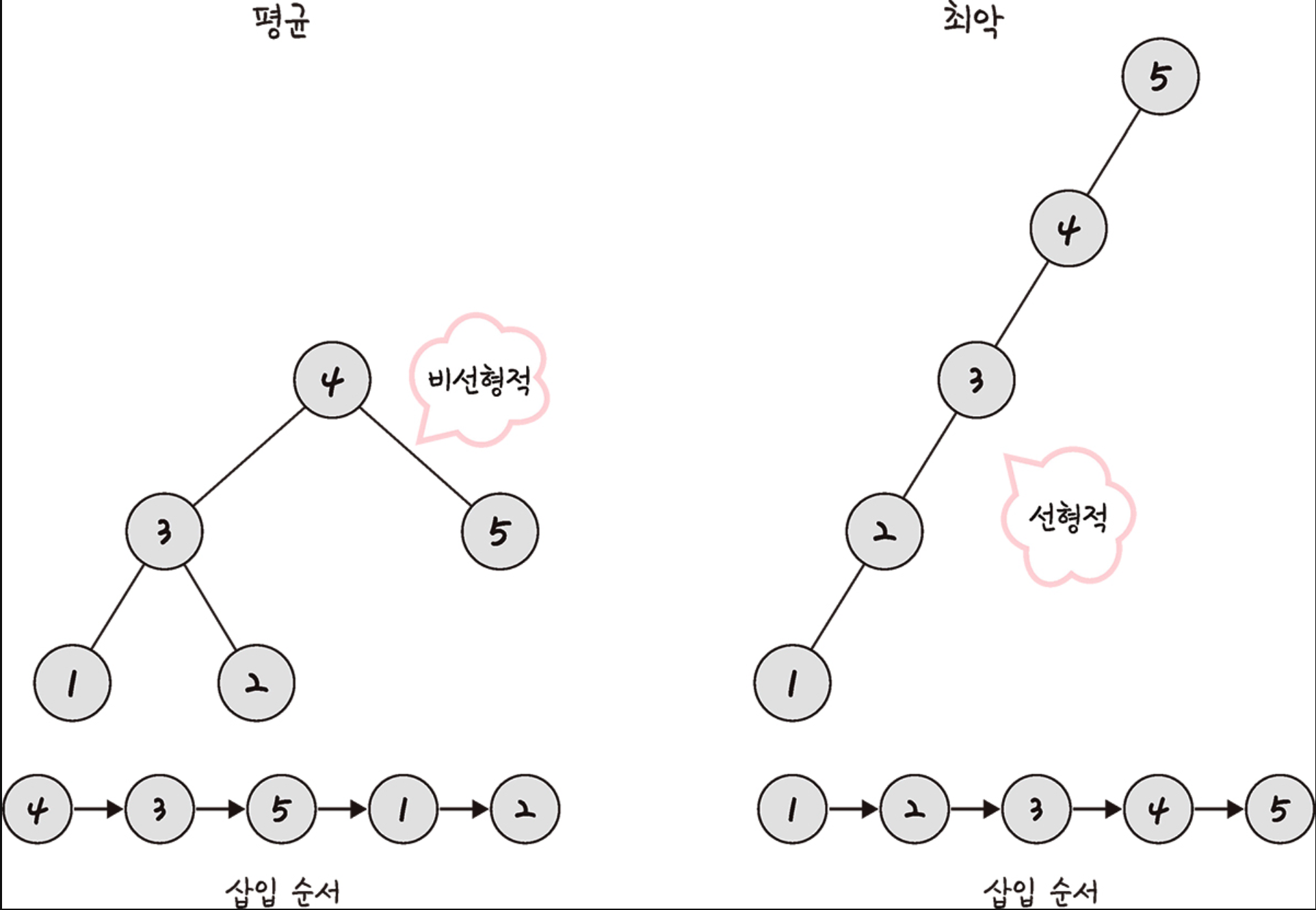
이진 탐색 트리는 특정 순서로 요소를 삽입하면 트리의 구조가 달라질 수 있다.
- 비선형적 이진 탐색 트리(Non-linear Binary Search Tree): 보통 요소를 찾을 때 O(logn)이 걸린다.
- 선형적 이진 탐색트리(Linear Binary Search Tree): 최악의 경우 O(n)이 걸린다.
AVL 트리
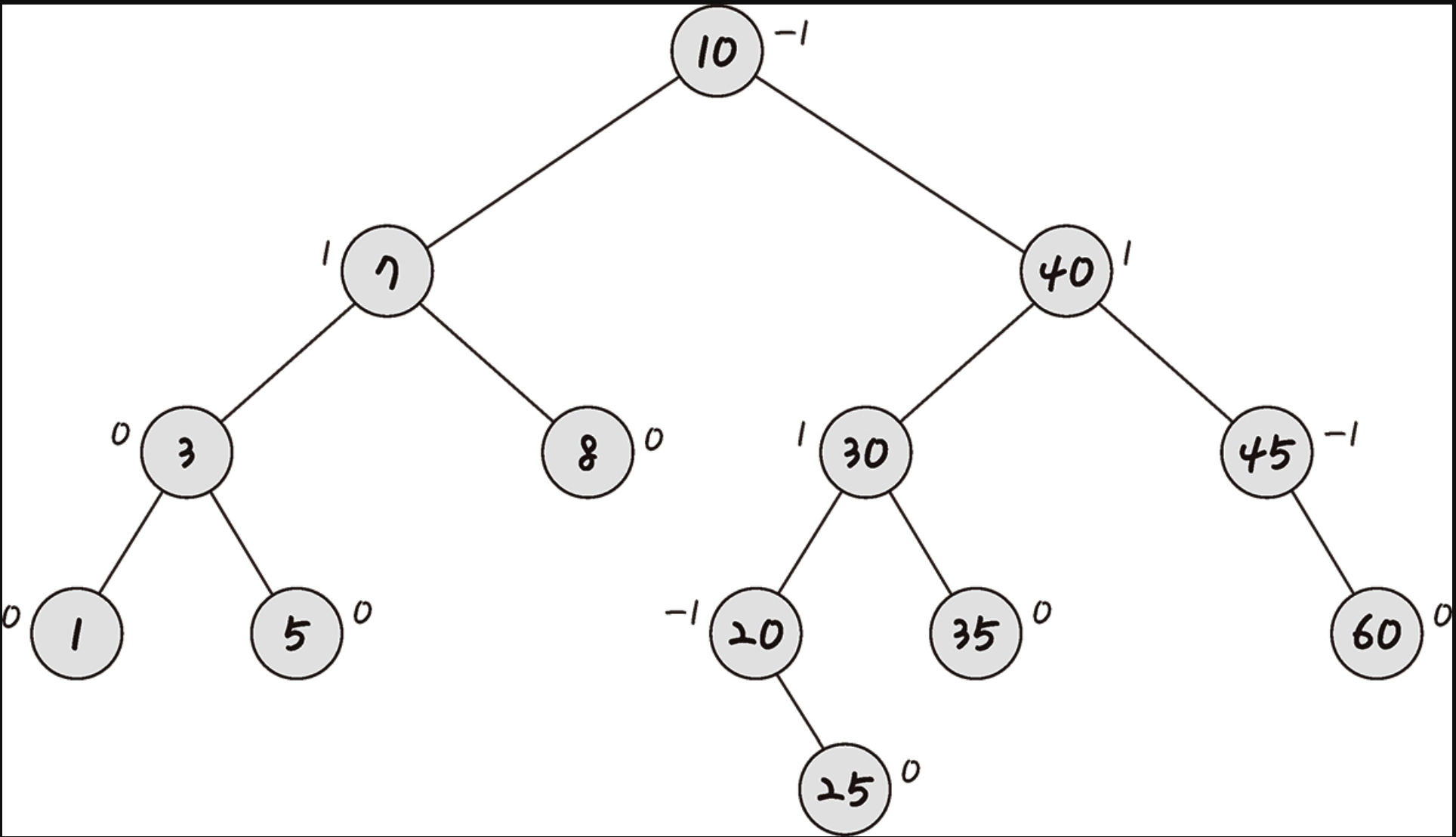
- 선형적인 트리가 되는 것을 방지하고자 스스로 균형을 잡는 이진 탐색 트리이다.
- 두 자식 서브트리의 높이는 항상 최대 1만큼 차이 난다.
- 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)이다.
레드 블랙 트리
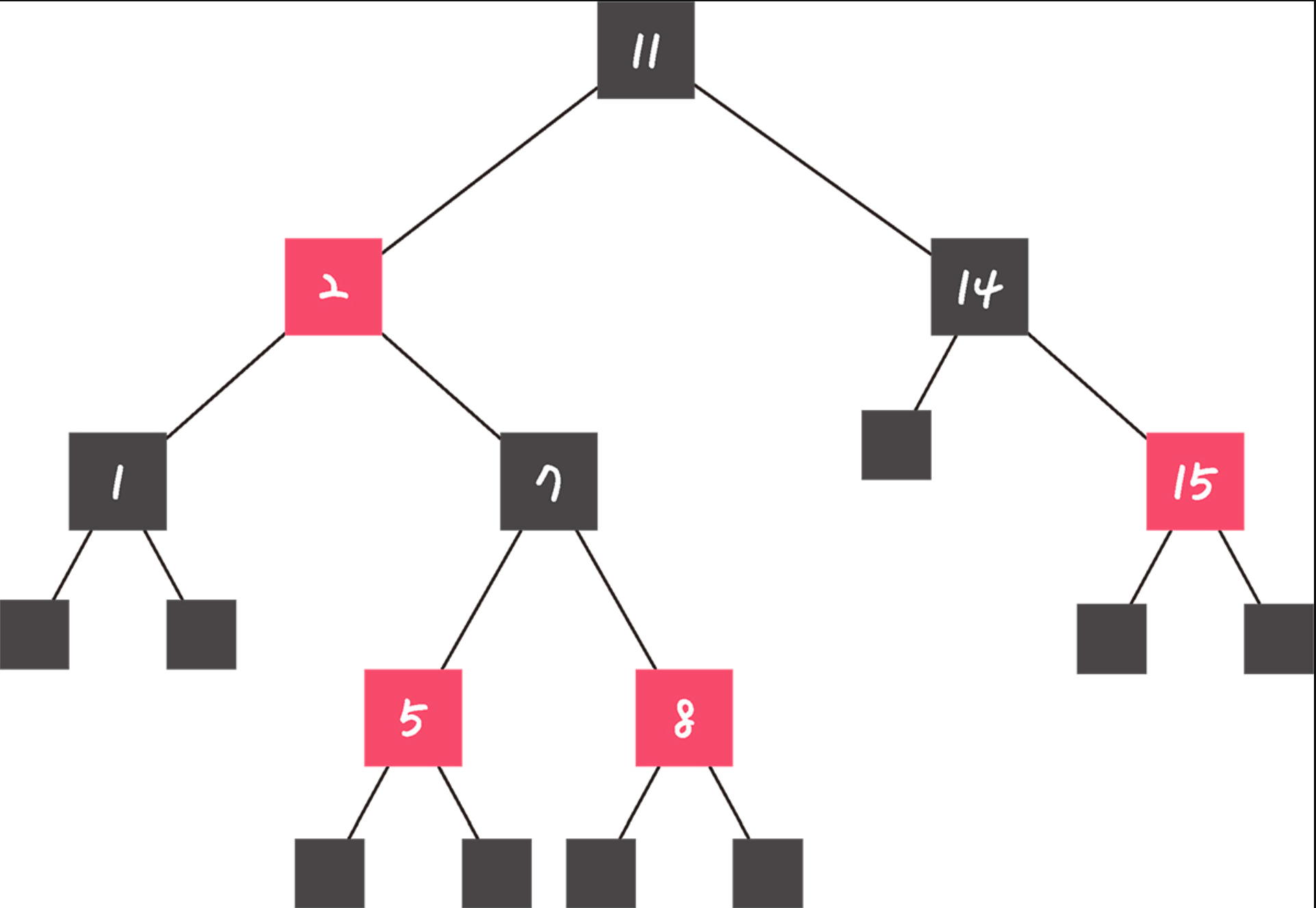
- 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하며, 삽입 및 삭제 중에 트리가 균형을 유지하도록 하는 데 사용된다.
- 모든 리프 노드와 루트 노드는 블랙이고 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다.
- 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)이다.
5.3.3 힙(Heap)
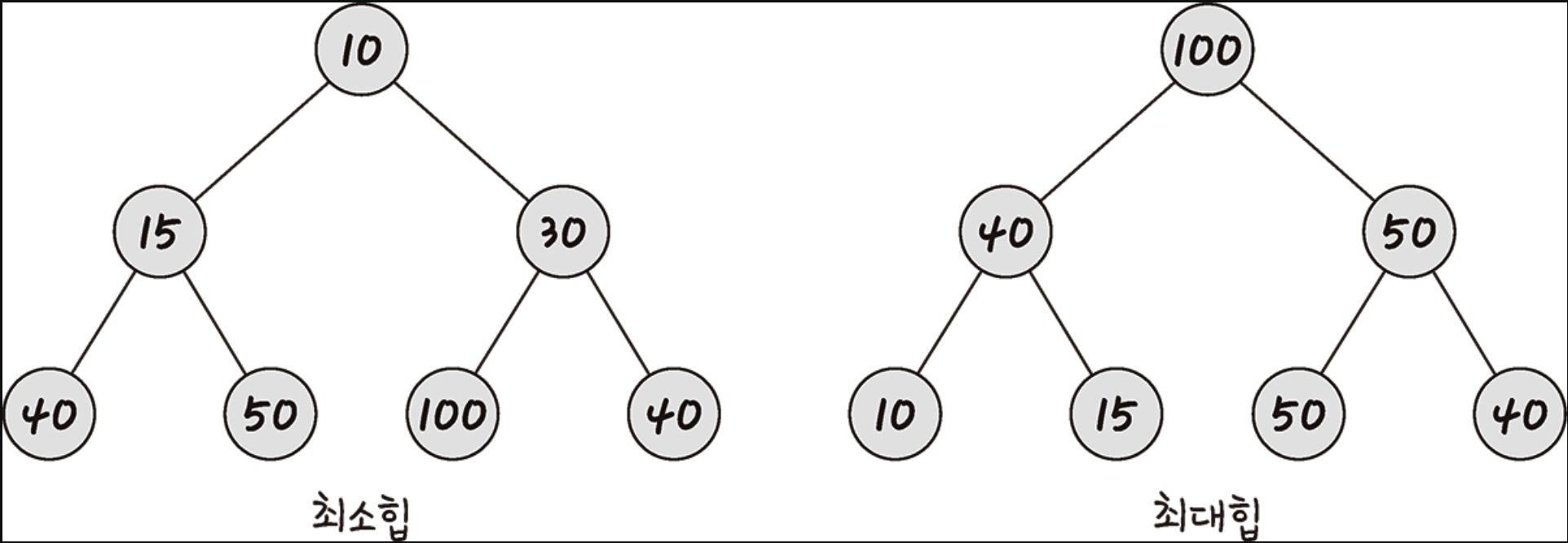
힙은 완전 이진 트리 기반의 자료 구조이며, 최소힙과 최대힙 두 가지가 있고 해당 힙에 따라 특정한 특징을 지킨 트리를 말한다.
- 최대힙: 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 한다.
- 최소힙: 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 작아야 한다.최대힙과 최소힙 모두 특정 노드에서 자식 노드와의 관계도 해당 특징이 재귀적으로 이루어져야 한다.
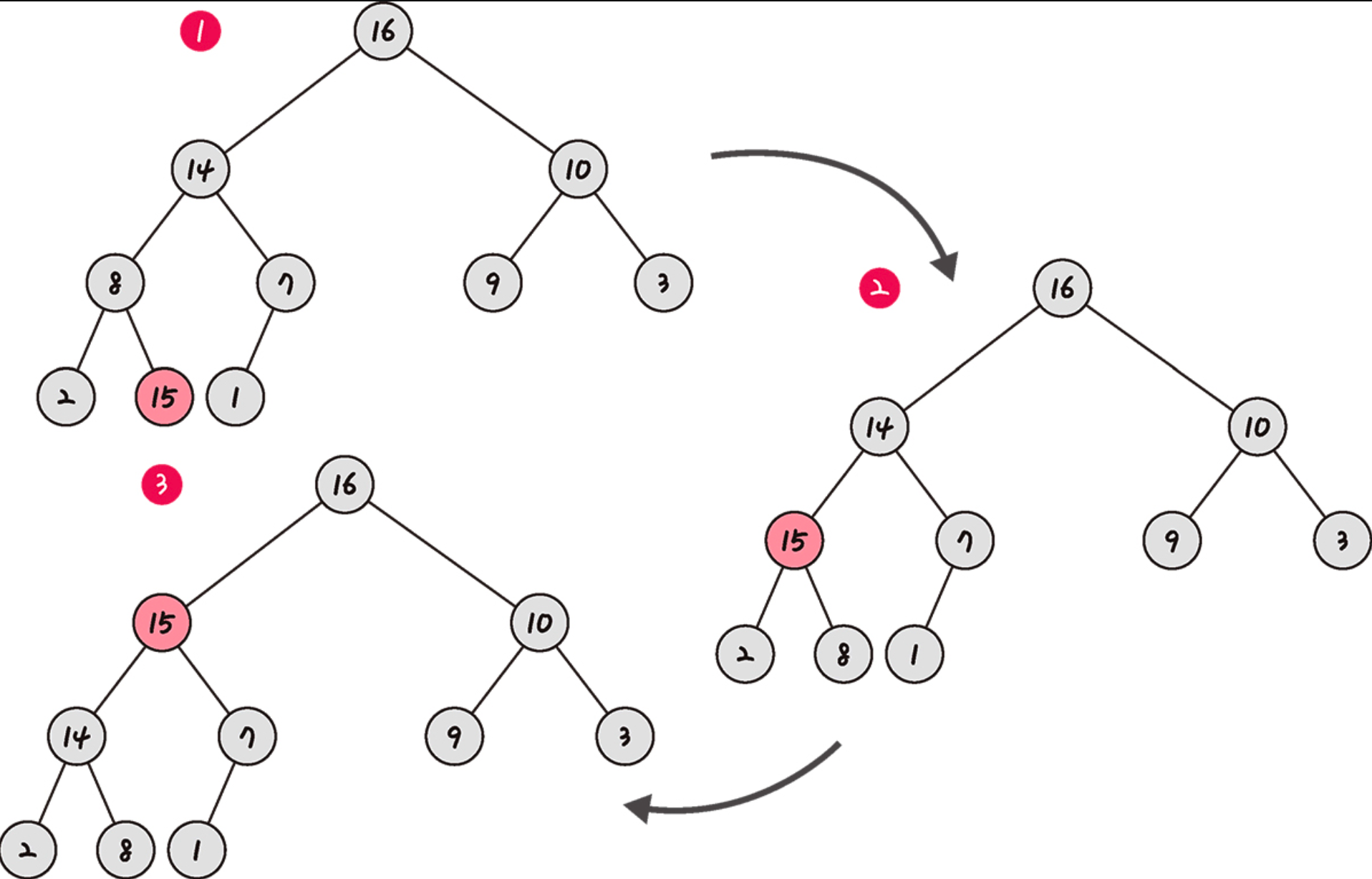
최대힙의 삽입
- 새로운 요소를 힙의 마지막 노드에 추가한다.
- 새로운 요소를 부모 노드들과 비교하며, 부모 노드보다 크다면 두 노드를 교환한다. 이를 반복하여 새로운 요소가 자신의 위치를 찾을 때까지 진행한다.
- 힙의 성질을 만족할 때까지 계속해서 요소를 부모 노드와 비교하며 교환하는 과정을 반복한다.
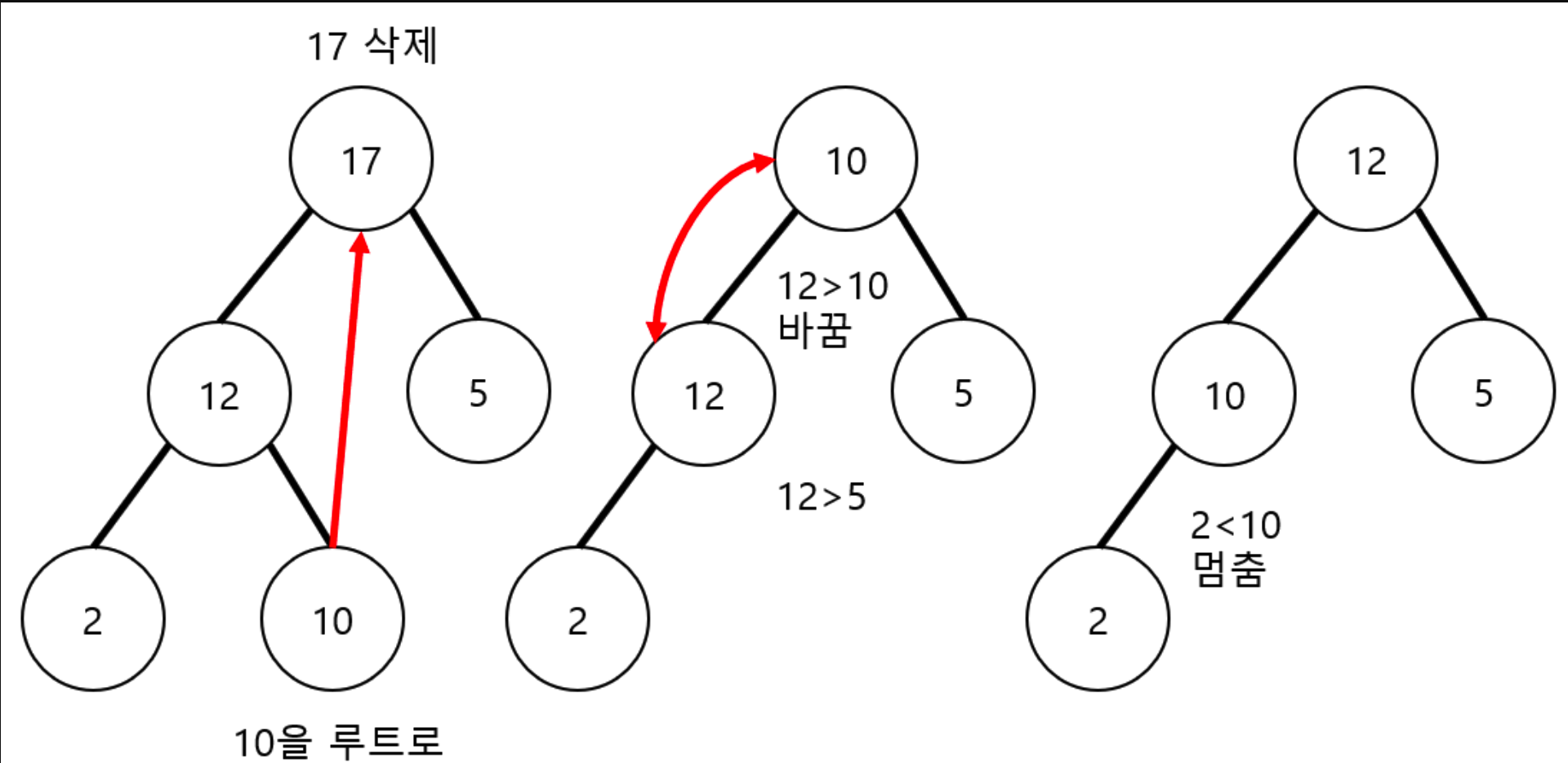
최대힙의 삭제
- 최대힙에서 최댓값은 항상 루트 노드에 위치하게 된다.
- 루트 노드를 삭제하고, 힙의 마지막 노드를 루트 노드의 위치로 가져온다.
- 새로운 루트 노드를 자식 노드들과 비교하며, 두 자식 노드 중 더 큰 값과 비교하여 자식 노드와 교환한다. 이를 반복하여 새로운 루트 노드가 자신의 위치를 찾을 때까지 진행한다.
- 힙의 성질을 만족할 때까지 계속해서 노드를 자식 노드와 비교하며 교환하는 과정을 반복한다.
5.3.4 우선순위 큐(Priority Queue)
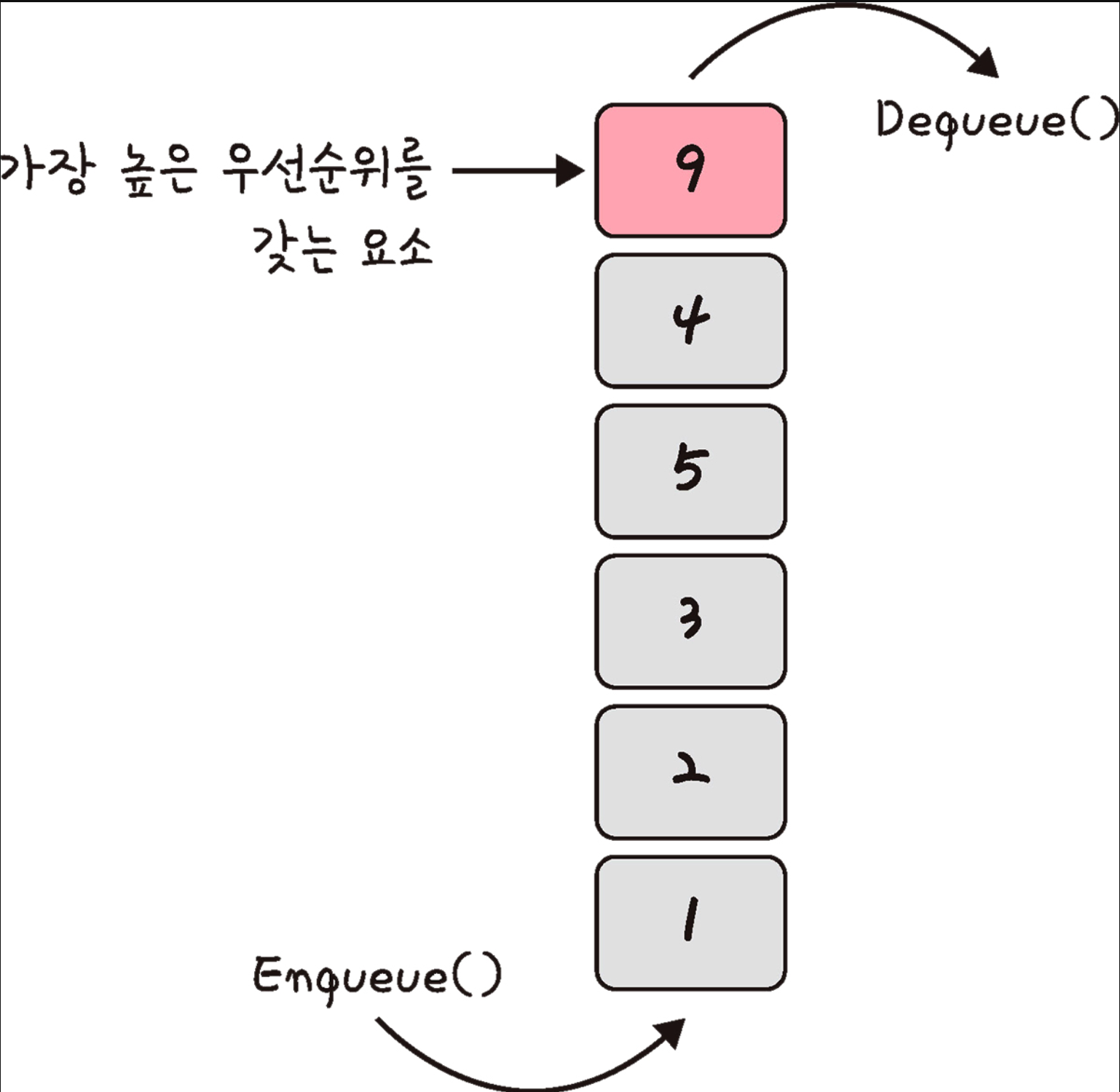
- 우선순위 큐는 일반적으로 힙(heap)이라는 자료 구조를 기반으로 구현된다.
- 우선순위 대기열이라고도 한다. 우선순위에 따라 작업이나 요소를 처리하는 대기열을 의미한다.
- 대기열에서 우선순위가 높은 요소가 우선순위가 낮은 요소보다 먼저 제공되는 자료 구조이다.
5.3.5 맵(Map)
- 맵은 키와 값을 쌍으로 저장하는 자료 구조이다. 하나의 키는 하나의 값에 대응된다.
- 맵에서 키는 유일해야 한다. 값에 접근하거나 값을 변경하는데 사용되기 때문이다.
- 맵은 중복된 값을 허용한다. 서로 다른 키에 대해 같은 값을 가질 수 있다는 의미이다.
- 주로 String : int 형태로 값을 할당해야할 때 사용한다.
- 자바에서 Map을 사용하기 위해 HashMap과 TreeMap 등의 클래스를 활용한다.
- HashMap
해시 기반으로 요소를 저장한다. 순서가 중요하지 않은 경우에 사용된다.
검색, 삽입, 삭제에 평균적으로 O(1)의 시간 복잡도를 가진다.- TreeMap:
요소를 정렬된 순서로 저장한다. 정렬된 집합을 필요로 할 때 사용된다.
삽입, 조회, 수정, 삭제의 연산에 O(log n)의 시간 복잡도를 가진다.
5.3.6 셋(Set)
- 셋은 동일한 요소를 중복해서 저장하지 않는 자료 구조이다. 동일한 값을 가진 요소를 추가하려고 하면 무시된다.
- 주로 중복을 제거하고 고유한 값만을 유지하려는 경우에 사용된다.
- 자바에서 Set을 사용하기 위해 HashSet과 TreeSet 등의 클래스를 활용한다.
- HashSet:
해시 기반으로 요소를 저장한다. 순서가 중요하지 않은 경우에 사용된다.
검색, 삽입, 삭제에 평균적으로 O(1)의 시간 복잡도를 가진다.- TreeSet:
요소를 정렬된 순서로 저장한다. 정렬된 집합을 필요로 할 때 사용된다.
삽입, 조회, 수정, 삭제의 연산에 O(log n)의 시간 복잡도를 가진다.
5.3.7 해시 테이블
- 해시 테이블은 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블이다.
- 삽입, 삭제, 탐색 시 평균적으로 O(1)의 시간 복잡도를 가지며 unordered_map으로 구현한다.
- 작은 크기의 캐시 메모리로도 프로세스를 관리하도록 할 수 있다.
