💡 백준 1120: 문자열
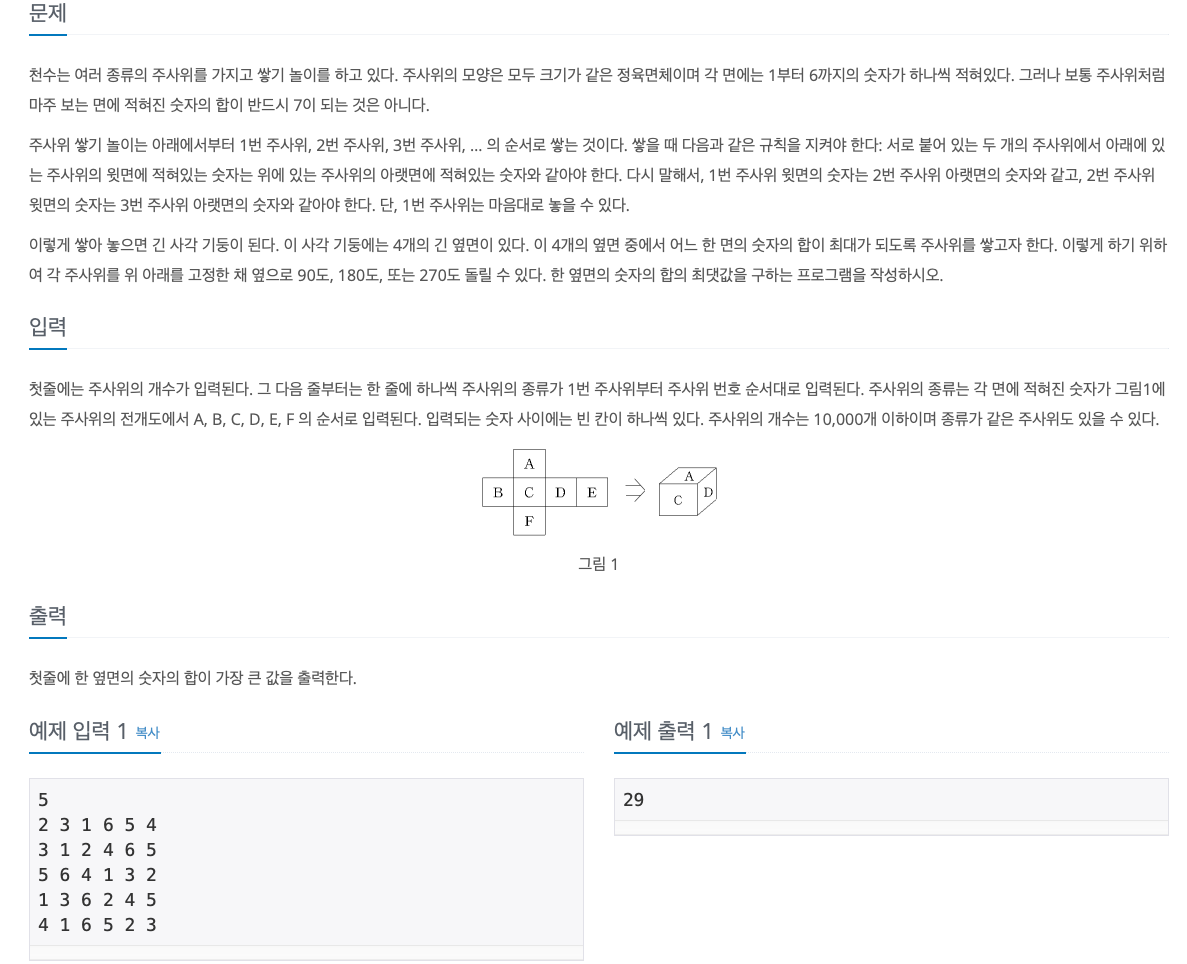
아래, 위 2면을 제외한 옆 4면 중 한 면을 일렬로 세울 수 있는 경우 중 합이 가장 큰 경우를 찾아 출력
🌱 코드 in Python
알고리즘: Brute Force
import sys
t = int(sys.stdin.readline())
dice_list = [list(map(int, sys.stdin.readline().split())) for i in range(t)] # 주사위 2차원 배열로 저장
max_sum = 0 # 출력값 초기화
def find_max(dice, bottom): # 탐색할 주사위 배열, 그 주사위의 아랫면에 있어야 할 숫자를 인자로 받음
for i in range(6):
if dice[i] == bottom: # 전달받은 주사위 배열을 돌며 아랫면 숫자가 있는 인덱스 판별
break
if i == 0: # 아랫면 인덱스가 0일 경우
return(dice[5], max(dice[1], dice[2], dice[3], dice[4])) # 이 주사위의 윗면이자 다음 주사위의 아랫면은 5번 인덱스가 되며, 나머지 남은 4면 중 가장 큰 값이 해당 주사위의 옆면이 됨
elif i == 1:
return (dice[3], max(dice[0], dice[2], dice[4], dice[5]))
elif i == 2:
return (dice[4], max(dice[0], dice[1], dice[3], dice[5]))
elif i == 3:
return (dice[1], max(dice[0], dice[2], dice[4], dice[5]))
elif i == 4:
return (dice[2], max(dice[0], dice[1], dice[3], dice[5]))
elif i == 5:
return (dice[0], max(dice[1], dice[2], dice[3], dice[4]))
for i in range(1, 7): # 가장 첫번째 주사위의 1 ~ 6 숫자 중 어떤 숫자를 처음 아랫면으로 놓고 시작했을 때 가장 큰 값이 되는 지 파악하기 위해 for 문 순회
n_bottom = i # 첫번째 주사위의 아랫면 숫자 결정
sum = 0 # 매 반복문의 합 초기화
for j in range(t): # 주사위의 갯수만큼 반복
n_bottom, ret = find_max(dice_list[j], n_bottom) # 탐색할 주사위, 그리고 그 주사위의 new_bottom을 전달하고, 반환값으로 다음 주사위의 new_bottom과 최대값을 받음
sum += ret # 탐색한 주사위의 최댓값 합산
if max_sum < sum: # 첫번째 주사위의 1 ~ 6을 하나씩 아랫면으로 둔 경우의 수마다 최댓값이 큰 경우 갱신
max_sum = sum
print(max_sum)각 주사위면은 전개도에 따라 0 - 5, 1 - 3, 2 - 4면이 마주보게 되며,
이번 주사위의 아랫면과 마주보고 있는 윗면의 숫자가 다음 주사위의 아랫면 숫자가 되는 조건을 가지고 있다
예를들어 맨 처음 주사위의 아랫면이 dice[0]일 경우 윗면은 dice[5]가 되고,
이 dice[5]에 있는 숫자가 다음 주사위에 어디에 적혀있느냐에 따라 다음 주사위의 아랫면과 윗면의 위치가 결정되는 것이다
첫번째 주사위의 아랫면이 결정되면 연속적으로 주어진 주사위의 아랫면과 윗면이 확정되기 때문에,
매 주사위마다 그 2면을 제외한 나머지 4면 중 가장 최댓값을 판별하여 그들의 합을 구해야 한다
첫번째 주사위의 아랫면은 1 ~ 6까지 총 6개의 경우가 있으며 이 모든 경우를 순회하며 최댓값을 찾으면 된다
🧠 기억하자
생각해보면 꽤나 확정되어있는 부분이 많고, 반복해야 하는 구간이 명확한 문제였는데 푸는데 시간이 아주 오래 걸렸다
무엇을 반복하고, 무엇이 확정되며, 무엇을 값으로 할 것인지를 문제에서 빨리 파악해야 할 것 같다
이번 문제의 경우 첫번째 주사위에 따라 다음 주사위들의 아래, 윗면이 고정된다는 점을 파악하는 것이 관건이었던 것 같다
다만 이 문제가 조금 더 헷갈렸던 것은 주사위의 숫자 배열과 전개도상의 인덱스가 일치하지 않아 그를 어떻게 주고 받을 것인가였다
앞으론 더 빨리 문제를 해결할 수 있었으면 좋겠다!

