[Algorithm] 백준 2839 - 설탕 배달 in Python(파이썬)

💡 백준 2839:

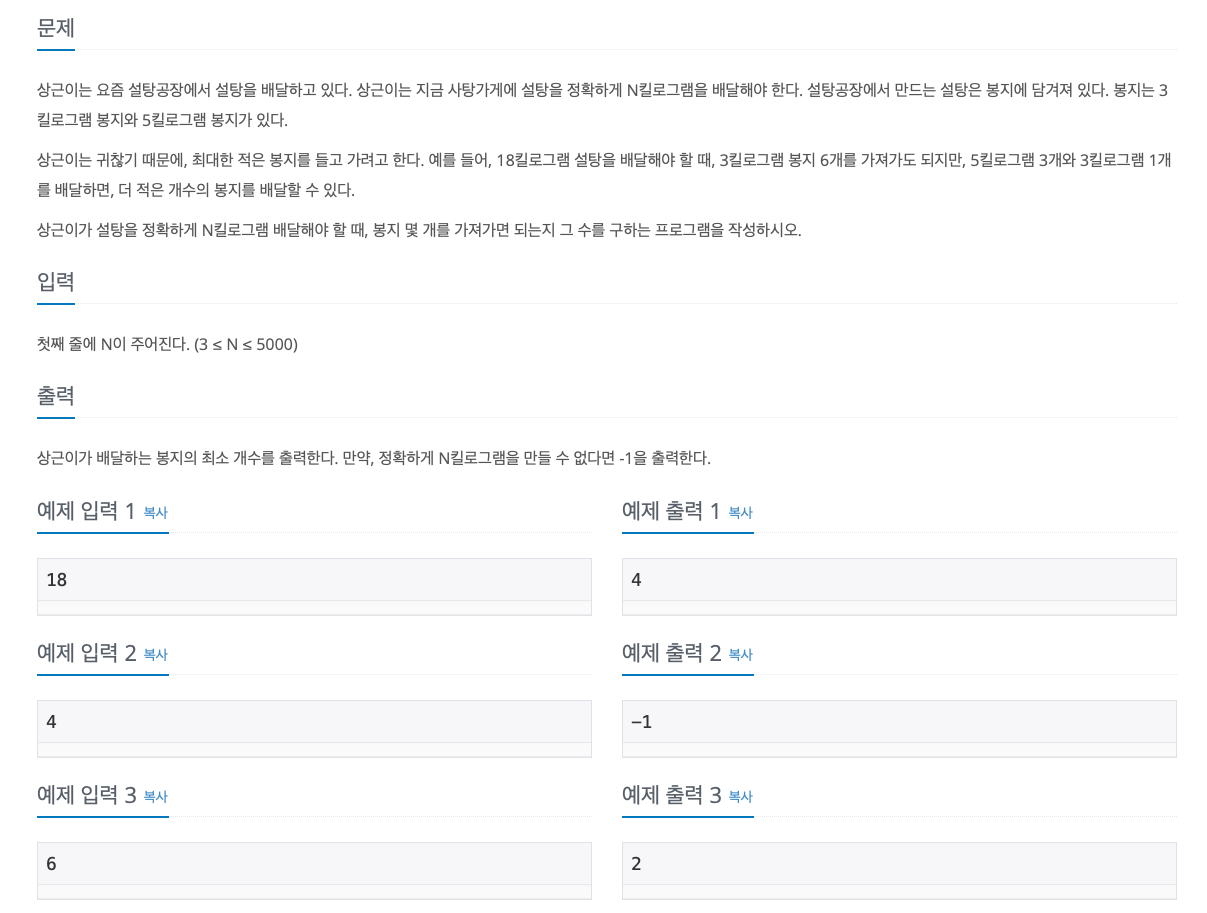
5의 배수의 경우 5로 나눈 값, 3의 배수이거나 5와 3을 더해 만들 수 있는 수의 경우 3항 전의 값에 하나를 더하여 계산

🌱 코드 in Python

알고리즘: Dynamic Programing

import sys

n = int(sys.stdin.readline())
dp = [-1] * (n + 1) # dp 배열 초기화
dp[3] = 1 # 3에 대해 값 초기화
for i in range(5, n + 1): # 5부터 n까지 순회
	if i % 5 == 0: # 5의 배수일 때
		dp[i] = i // 5 # 5로 나눈 몫 저장
	elif dp[i - 3] != -1: # 3개 전 항의 값이 -1이 아닌 즉, 유효한 값일 경우 해당 값에 + 1
		dp[i] = dp[i - 3] + 1
print(dp[n])

5의 배수일 경우에는 5kg 봉지만으로 배달하는 것이 최선의 값이지만, 3의 배수는 3kg 봉지가 늘 최선일 수는 없으며, 5 또는 3의 배수가 아니지만 두가지를 활용하여 만들 수 있는 경우가 있다

가령 18kg의 경우 3kg 6봉지도 가능하지만, 5kg 3봉지와 3kg 1봉지로 가능하다
또한 11kg의 경우 5 또는 3의 배수는 아니지만 5kg 1봉지와 3kg 2봉지로 가능하다

따라서 5로 나누어 질 경우 그 몫을 늘 최적해로 저장해두고,
3전항의 값이 유효한 값을 가지고 있을 경우 3kg 봉지 하나를 추가하는 식으로 코드를 짜면
최적값을 알 수 있다

🧠 기억하자

이 문제는 그래도 다른 문제들에 비해 수월하게 문제를 풀었다
딱히 중요하게 파악해야 할 부분은 없었음!

백준 2839 바로가기