[TIL] 버블, 선택, 삽입 정렬

버블 정렬

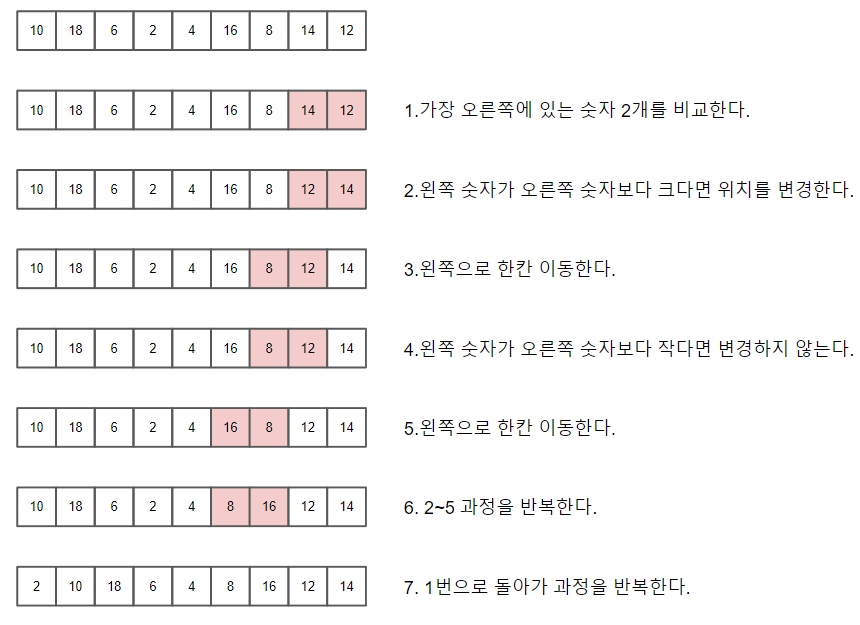
배열의 길이가 N일 경우, 버블 정렬은 N-1의 요소를 비교해야 한다. 최악의 경우 모든 요소들의 위치를 변경해야 하기 때문에 효율적인 정렬 알고리즘이 아니다.

⏰ 시간 복잡도 : O(n^2)

구현 코드

public String solution(int n, int[] arr) {
        // 버블 정렬 
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n-1; j++) {
                if(arr[j] > arr[j+1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        for(int x : arr) {
            sb.append(x).append(" ");
        }

        return sb.toString();
    }

선택 정렬

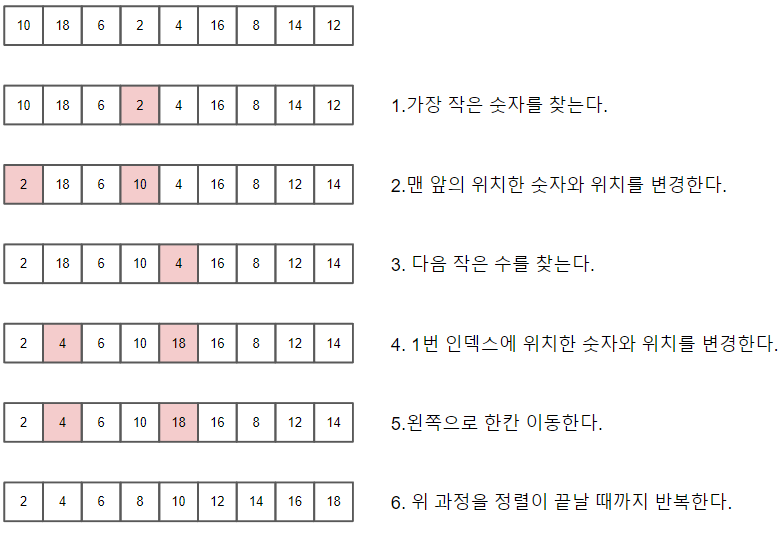
정렬되지 않은 배열에서 가장 작은 수를 가진 요소를 찾아야 하기 때문에 배열의 길이가 N일 경우 N-1번의 비교를 한다.

이 부분은 버블 정렬과 동일하지만 버블 정렬과 달리 선택 정렬은 N번의 위치 이동을 실행하지 않고 반복에 한번 위치 이동을 한다.

⏰ 시간 복잡도 : O(n^2)

구현 코드

public String solution(int n, int[] arr) {
        // 선택 정렬 -> 가장 작은 수를 찾아 i번쨰 자리에 j 숫자로 위치를 변경한다.
        for(int i = 0; i < n; i++) {
            for(int j = i+1; j<n; j++) {
                int min = Integer.MAX_VALUE;
                if(min > arr[j]) min = arr[j];
                if(min < arr[i]) {
                    int tmp = arr[i];
                    arr[i] = min;
                    arr[j] = tmp;
                }
            }
        }
        StringBuilder sb = new StringBuilder();
        for(int x : arr) {
            sb.append(x).append(" ");
        }

        return sb.toString();
    }

삽입 정렬

모든 아이템을 스캔하는 선택 정렬과 달리 삽입 정렬은 필요한 아이템만 스캔하기 때문에 선택 정렬보다 더 나은 성능을 보인다.

하지만 삽입 정렬이 버블, 선택 정렬보다 빠르다 하더라도 시간 복잡도는 동일하게 O(n^2)이다.

시간 복잡도는 최악의 경우를 생각하기 때문에 평균 시간 복잡도를 고려해야 한다.

버블, 선택 정렬은 최고의 경우에도 O(n^2)를 나타내는 반면, 삽입 정렬은 최고의 경우 O(n)의 시간 복잡도가 나타난다.

⏰ 시간 복잡도 : 최선 : O(n), 최악 O(n^2)

구현 코드

public String solution(int n, int[] arr) {
        // 삽입정렬
        for(int i = 0; i < n; i++) {
            int tmp = arr[i];
            for(int j = i-1; j >= 0; j--) {
                if(arr[j] > tmp) {
                    arr[j+1] = arr[j];
                    arr[j] = tmp;
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        for(int x : arr) {
            sb.append(x).append(" ");
        }

        return sb.toString();
    }

🤔 정렬은 봐도봐도 헷갈리기 때문에 주기적으로 복습을 해야...