[TIL] 백준 2747 피보나치 수(DP)

문제

해결 방법

재귀함수

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        System.out.println(fibonacci(n));
    }
     static int fibonacci (int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;

        return fibonacci(n-1) + fibonacci(n-2);
    }
}

피보나치는 재귀함수를 사용하면 쉽게 해결할 수 있다. 다만 재귀함수를 사용할 경우의 시간 복잡도는 O(2^N)로 숫자가 커질수록 비효율적이라는 단점을 가진다.

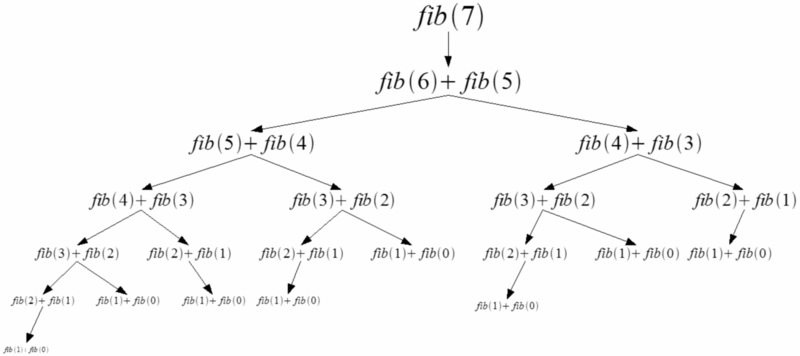
위 그림을 보면 같은 수에 대한 계산을 이미 진행했음에도 다음 수를 위해 반복적으로 계산하게 된다.

동적 계획법(Dynamic Programming)

동적계획법이란 큰 문제를 작은 여러개의 문제로 나누어 푸는 기법이라고 한다.

동적계획법의 특징 중 하나는 작은 문제로 쪼개진 여러개의 문제들에 대한 값을 어딘가에 저장해두고 같은 계산을 해야할 때 저장해둔 값을 가져와 사용한다는 점이다.

💡 이러한 특징을 메모리제이션이라고 한다.

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        // 값을 저장할 배열
        int[] memo = new int[46];
        int n = Integer.parseInt(br.readLine());

        System.out.println(fibonacci(n, memo));

    }
    static int fibonacci(int n, int[] memo) {
        if(n <= 1) {
            return n;
        } else if (memo[n] != 0) {
            // memo[n]의 값이 0이 아닐 경우, 이미 계산된 숫자
            return memo[n];
        } else {
           // memo[n]의 값이 0일 경우, 재귀함수를 돌린다.
            return memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo);
        }
    }
}

위와 같은 방법을 사용하면 불필요하게 같은 작업을 여러번 수행할 필요가 없기 때문에 시간복잡도가 O(N)으로 줄어든다.