시간 복잡도(Time Complexity)

• 효율적인 알고리즘은 무엇일까?
  • 정해진 코드를 수행하는 시간은 개개인의 컴퓨터 하드웨어 성능에 따라 달라질 수 있다.
  • 시간보다는 코드가 완료될 때까지 절차의 수가 더 적은 것이 효율적이라고 할 수 있다.

💡시간 복잡도
: 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?

시간 복잡도의 종류

1. Big-O(빅-오)
   • 최악의 경우에 대해여 나타내는 방법
   • 가장 많이 사용된다.
2. Big-Ω(빅-오메가)
   • 최선의 경우에 대해여 나타내는 방법
3. Big-θ(빅-세타)
   • 중간(평균)의 경우에 대해여 나타내는 방법

💡 최선의 방법을 강구하여 해결하는 것이 바람직하지만 결과를 반환하는데 최선은 1초, 최악은 1시간이 걸린다고 했을 때, 최선의 방법만 생각하면 최악의 결과가 나왔을 때 문제가 없는 코드임에도 문제가 있다고 판단하여 그 문제를 파악하는데 많은 시간을 소요할 수 있다.
=> 최악 (Big-O) 의 상황을 고려하여 대비하는 것이 바람직!

Big - O

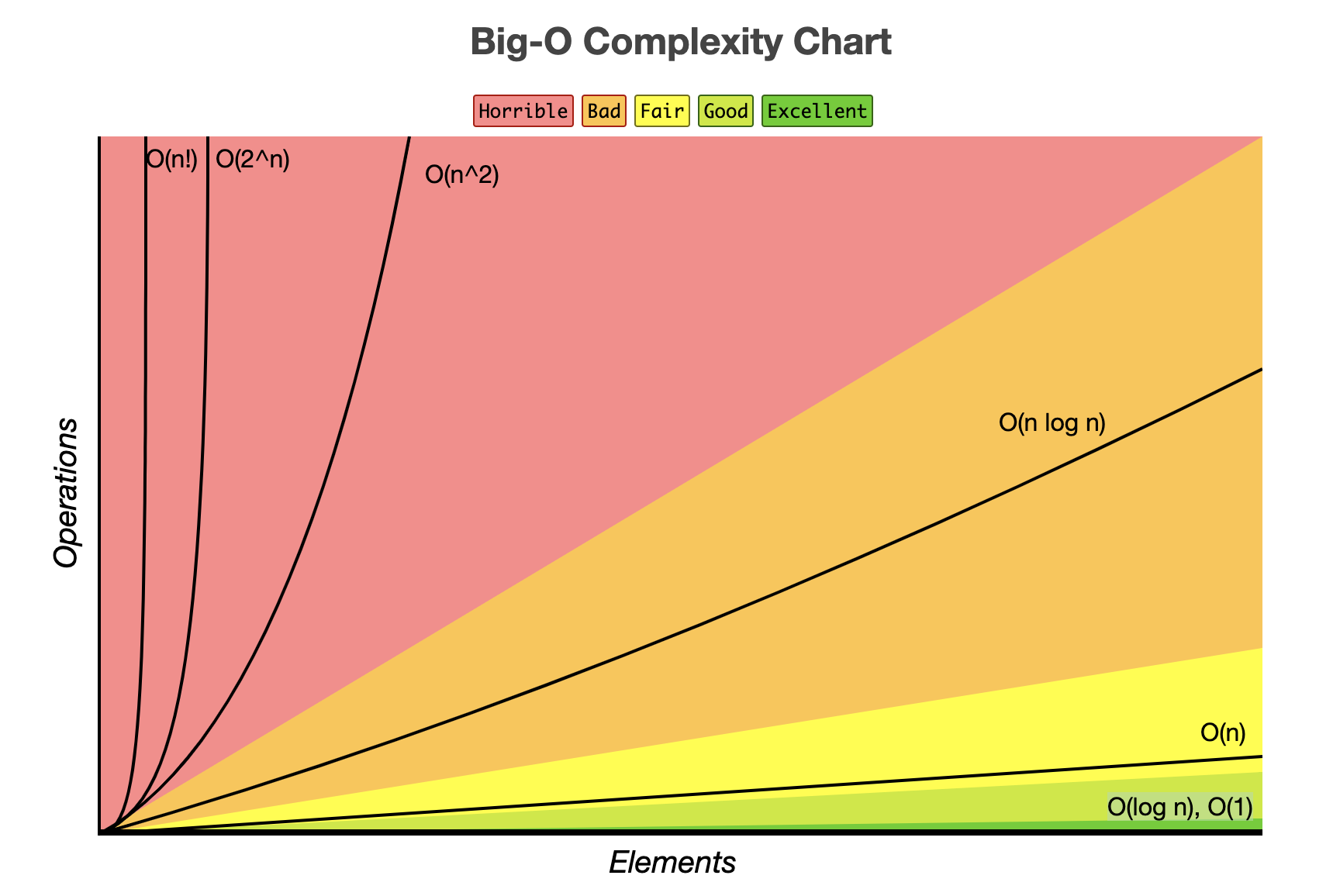
Big - O를 사용하는 이유
1. 알고리즘을 빠르게 분석하기 위해
2. 어떤 로직을 사용할 것인지 쉽게 파악하기 위해

💡 n = 입력값의 수
💡 O(함수) = 입력값에 따른 연산 횟수

O(1) : constant complexity

• 입력값이 증가해도 연산 횟수는 늘지 않는다.
  • 입력값의 크기와는 상관없이 바로 출력값을 얻어낼 수 있다.

return arr[index];
// 바로 index위치에 있는 값을 출력해준다.

O(n) : linear complexity

• 입력값이 증가함에 따라 연산 횟수도 같은 비율로 증가한다.
  • 입력값 1개, 연산 1개 -> 입력값 100개 -> 연산 100개

for(int i=0; i < arr.length; i++) {
....
}
// 입력값 수마다 연산을 실행한다.

O(log n) : logarithmic complexity

• logab = x : a를 x만큼 거듭제곱한 값이 b다
• log의 지수 2는 생략되어 있다.
• O(1) 다음으로 빠른 시간복잡도를 가진다.
• BST(이진탐색트리)의 방식

O(n^2) : quadratic complexity

• 입력값이 증가함에 따라 연산 횟수가 n의 제곱근의 비율로 증가한다.

or(int i = 0; i < n; i++) {                // n^1
		for(int j = 0; j < n; j++) {       // n^2
			// do something for 1 second
		}
	}

O(2^n) : exponential complexity

• 입력값이 증가함에 따라 연산 횟수가 2의 n 제곱근의 비율로 증가한다.
• 가장 느린 시간 복잡도를 가진다.
• 구현하는 알고리즘이 이 복잡도를 가진다면 다른 방식으로 접근하는 것을 추천
• 재귀로 구현한 피보나치 수열이 대표적인 예이다.

데이터 크기에 따른 시간 복잡도

데이터 크기 제한	예상되는 시간 복잡도
n <= 1,000,000	O(n) or O(log n)
n <= 10,000	O(n2)
n <= 500	O(n3)

💡 가장 빠른/느린 시간 복잡도는 무엇일까요?
-> 빠른 것은 O(1),O(log n), 느린 것은 O(2^n)
💡효율적인 알고리즘을 구성했다 함은 무엇을 의미할까요?
-> 입력값 대비 적은 연산 횟수
💡시간 복잡도는 A와 B의 비례함이 어느 정도인지를 나타냅니다. A와 B는 무엇일까요?
-> 입력값과 연산 횟수