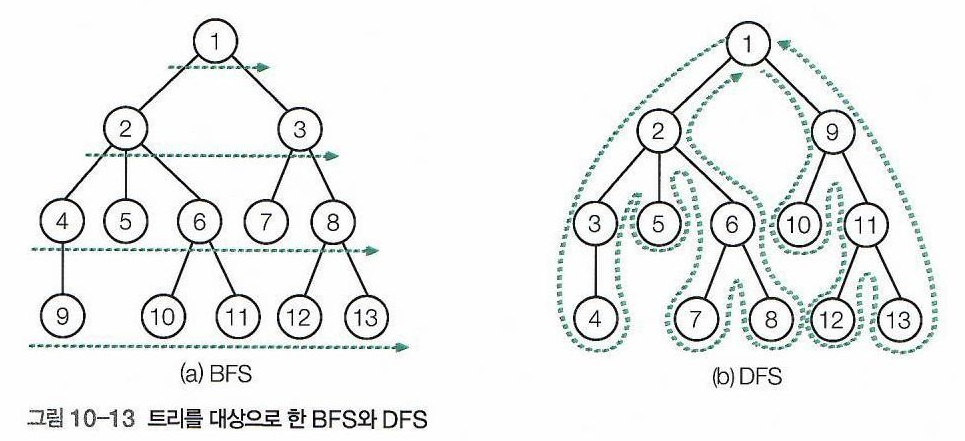
DFS와 BFS

• 그래프의 모든 정점을 방문해야 할 , 사용되는 자료구조 순회 방법이다.
• 어떤 노드에 방문했었는지 여부를 반드시 검사해야 한다. 하지 않는 경우에는 무한 루프에 빠질 위험이 있다.
• 그래프 내에 적은 숫자의 간선을 가지는 경우 인접 행렬 보다 인접 리스트를 사용하는 것이 유리

DFS (Depth-First Search) : 깊이 우선 탐색

💡 모든 노드를 방문하고자 하는 경우에 사용

• 경로의 특징을 저장하는 경우
• 검색 대상이 많을 경우

DFS의 개념

• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
• 하나의 정점에서 시작해 해당 경로를 끝까지 탐색한 후, 다음 경로로 넘어가 탐색하는 방법

DFS의 특징

1. 자기 자신을 호출하는 순환 알고리즘의 형태를 가진다.( 재귀함수 )
2. 전위 순회를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
3. BFS에 비해 간단하다.
   4.단순 검색 속도 자체는 BFS에 비해 느리다.

DFS의 구현방법

1. 순환 호출 이용(재귀)
2. 명시적인 스택 사용
   • 방문했던 정점을 저장했다 꺼내 쓰기 위해

BFS (Breadth-First Search) : 너비 우선 탐색

💡 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용

• 검색대상의 규모가 크지 않고 시작 지점으로부터 원하는 대상이 멀지 않을 경우

BFS의 개념

• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
• 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

BFS의 특징

• DFS에 비해 상대적으로 직관적이지 않다.
• 시작 정점에서부터 거리에 따라 단계별로 탐색
  - 0의 깊이를 가진 노드를 순회 -> 1의 깊이를 가진 노드를 순회 -> n의 깊이를 가진 노드를 순회
  
• 재귀적으로 동작하지 않는다.
• 방문한 노드들을 차례대로 저장한 후 꺼낼 수 있는 선입선출을 원칙으로 하는 큐(Queue)를 사용한다.

BFS의 구현방법

1. 자료구조 큐(Queue)를 이용