배경 지식
3차원 회전의 표현
컴퓨터 그래픽스에서 어떤 3차원 물체를 표현하는 기본적인 방법은, 그 물체 고유의 3차원 좌표계(frame)를 정하고, 해당 물체의 형태는 그 고유의 좌표계 안에서 표현을 하는 것이다. 이렇게 표현하게 되면 물체를 평행이동 하거나 회전을 시킬 때 해당 좌표계를 이동하거나 회전을 시킴으로써 간단하게 계산이 가능하다.
기본적인 3차원 좌표계는 서로 수직인 단위 벡터로 구성되어 있다.
행렬로 표현하기
3차원 에서의 선형변환은 행렬식으로 표현할 수 있다. 즉 회전변환도 행렬식으로 표현할 수 있다는 것이다. 이러한 행렬을 회전행렬 이라고도 부른다.
위와 같은 행렬을 직교행렬(Orthogonal matrix)라고 한다. 각각의 열벡터들은 서로 수직이며 크기가 1이기 때문이다. 직교행렬 중에서는 각각의 열벡터들의 크기가 -1 또는 1 인 경우가 있는데 이중 1인 경우를 특수직교행렬(Special orthogonal matrix) 라고 한다. 즉 우리가 최종 목표로 하는 회전변환은 특수직교행렬을 사용해야 한다는 것을 알 수 있다. 이렇듯 3차원 회전을 표현하는 가장 쉽고 간단한 방법은 행렬로 표현하는 것이다.
회전변환을 행렬로 표현할 때의 문제점
- 수치적으로 불안정(numerically unstable)하다. 앞서 언급했듯이 어떤 행렬이 회전 변환이 되기 위해서는 여러 가지 조건이 필요하다. 즉 컴퓨터로 표현할 때는 이 많은 조건을 매번 확인해야 한다는 뜻이고, 회전 변환을 여러번 거치게 되면 수치적으로 더 빠르게 불안정해질 수 있다는 의미이다.
- 회전축과 회전 각도를 알아내기 어렵다. 오직 행렬로부터 이 정보를 뽑아내기 위해서는 매우 복잡한 계산이 필요하고, 이는 수치적으로 불안하다는 문제와도 연관되어 있다.
💡 회전축과 회전 각도를 알아내는 것이 왜 필요할까?
가상의 캐릭터를 나타내는 동영상을 만든다고 가정했을 때, 모든 프레임별로 캐릭터를 그리는 것 보다, 중요한 장면만을 그린 뒤, 그 사이의 프레임들은 컴퓨터가 회전축과 회전각을 통해 유추해 낼 수 있기 때문이다.
오일러 각도
오일러 각도란 3차원 공간에서 물체가 놓인 자세를 표현하기 위해 나타내는 3개의 각도이다. 오일러 각도를 사용하는 이유는 어떠한 물체가 회전을 하고 난 후의 좌표를 구하기 위해 사용된다. 아래의 설명을 보면 이해가 쉽다.
좌표변환을 통해서 차근차근 알아보자
1번째 회전
1번째 회전은 x축을 기준으로 한 Roll 회전이고, 이를 1번째 오일러 각(1 Euler Angle)이라고 부른다. 현재의 x,y,z 좌표에서 x축을 기준으로 회전하여 새로운 x1, y1, z1을 얻게 된다. 이를 행렬식으로 나타내면
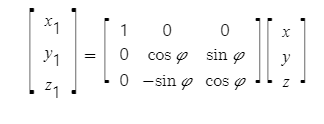
이렇게 회전행렬을 통해 두 좌표측 간의 관계를 나타낼 수 있다. 이를 간단히 표현하면
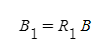
2번째 회전
2번째 회전은 y1축을 기준으로 한 Pitch 회전이고, 이를 2번째 오일러 각(2 Euler Angle)이라고 부른다. x1, y1, z1 좌표가 y1축을 기준으로 회전하여 새로운 x2, y2, z2를 얻게 된다. 이때 y1축을 기준으로 회전하였기 때문에 y1과 y2는 같은 값이다. 이를 행렬식으로 나타내면
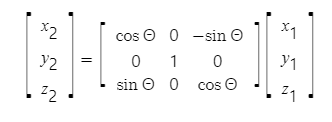
마찬가지로 회전행렬을 통해 두 좌표측 간의 관계를 나타낼 수 있다.
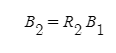
3번재 회전
3번째 회전은 z2축을 기준으로 한 Yaw 회전이고, 이를 3번째 오일러 각(3 Euler Angle)이라고 부른다. x2, y2, z2 좌표가 z2축을 기준으로 회전하여 새로운 x3, y3, z3를 얻게 된다.이때 z2축을 기준으로 회전하였기 때문에 z2와 z3는 같은 값이다. 이를 행렬식으로 나타내면
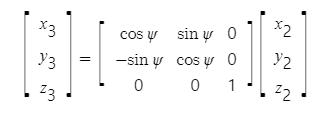
마찬가지로 회전행렬을 통해 두 좌표측 간의 관계를 나타낼 수 있다.
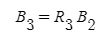
각각의 회전식을 대입하면 최종적으로 다음과 같은 식이 나오게 된다.
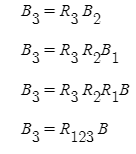
여기서 R123의 값을 계산해 보면 다음과 같이 나오게 된다.
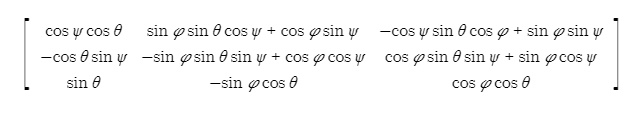
이렇게 우리는 1-2-3 순서(Roll-Pitch-Yaw 순서)로 회전을 진행 하였다. 하지만 가장 흔하게 쓰이는 순서는 3-2-1(Yaw-Pitch-Roll)순서 이다. 즉 R321 값을 구해야 한다. 이는 단순한 역행렬 계산으로 구할 수 있다.
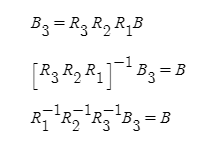
💡 여기서 R1 R2 R3모두 orthogonal한 matrix이기 때문에 역행렬을 쉽게 구할 수 있다.
이렇게 R321을 구해보면 다음과 같다.

참고문헌
https://m.blog.naver.com/droneaje/221999534231
https://tistory.joonhyung.xyz/16