Pseudo Inverse

Pseudo inverse가 무엇인지 간단하게 설명하자면, 역행렬은 full rank인 m x m 정방 행렬(square matrix)에서만 정의되는 반면 정방 행렬이 아닌 다른 모양의 행렬에서는 역행렬 대신에 유사 역행렬(pseudo inverse matrix)을 정의할 수 있다. 즉 어떠한 행렬의 역행렬을 구할 수 없을 때, 최대한 유사한 역행렬을 얻어낼 수 있는 것이 Pseudo inverse 이다.

4가지 경우의 수

Pseudo inverse는 정방 행렬이 아닌 경우일 때, 사용하는데 정방행렬이 아닌 경우는 총3가지 이다. 모든 경우의수를 살펴보자. 우선 이해를 돕기 위해 4가지 subspace를 첨부하였다.

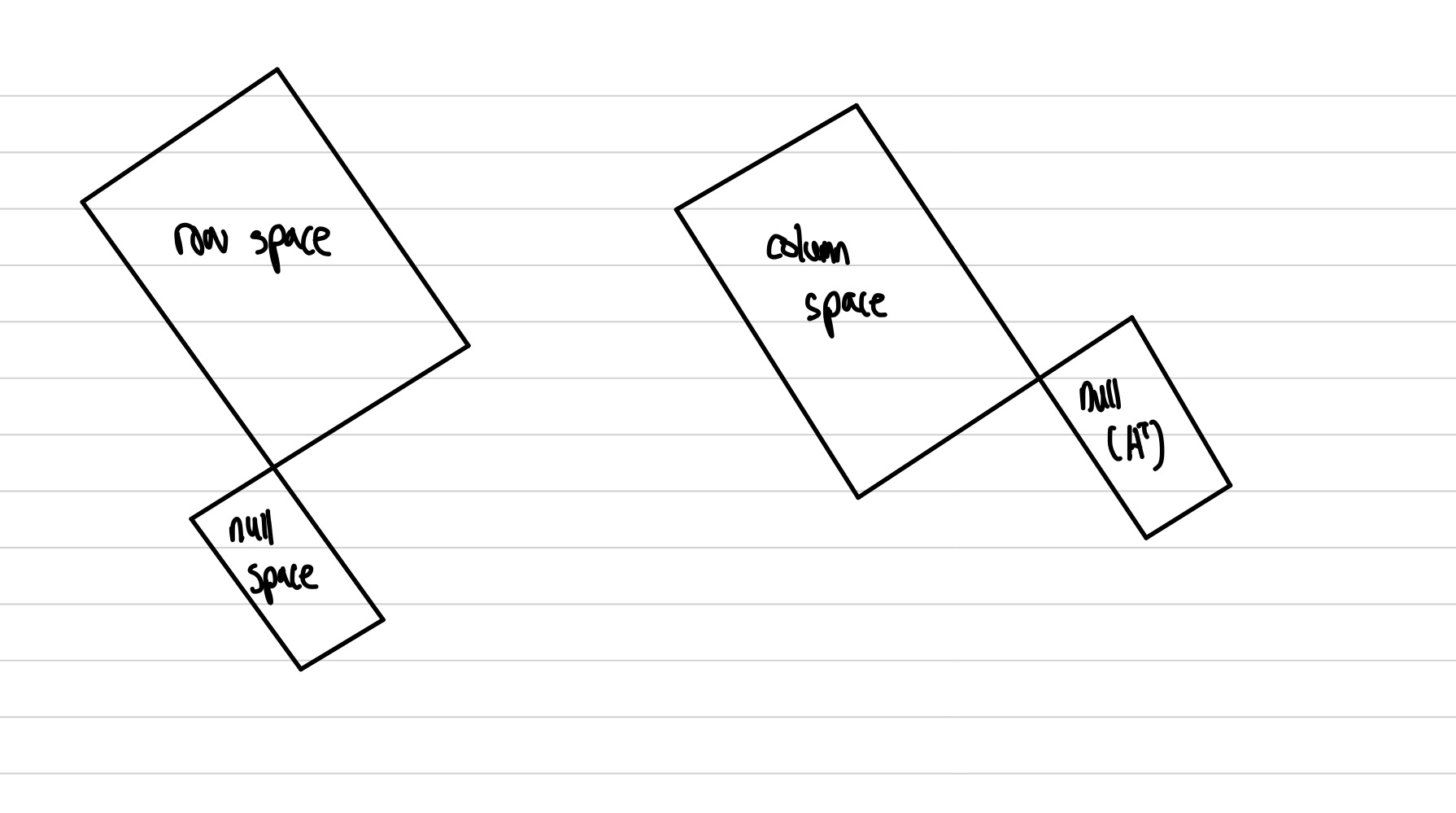
1. r = m = n

이는 정방행렬 인 경우로, $AA^{-1} = I = A^{-1}A$가 성립한다.

2. r = n < m

full colunm rank인 경우로, 이때 행렬의 null space의 dimension은 0이 된다. 즉 $Ax=B$를 만족하는 solution은 없거나, 1개이다.

우리가 직사각형 행렬을 보기좋게 만드는 방법을 알고 있다. $A^TA$를 통해 정방행렬로 만들 수 있다. 이렇게 정방행렬로 만들어준 후, 우리가 최종적으로 원하는 항등행렬을 만들어 보자.

이렇게 $A^TA$를 항등행렬로 만들어 주는 행렬을 left inverse matrix라고 부른다.

3. r = m < n

full row rank인 경우로, 이때 행렬의 left null space의 dimension은 0이 된다. 즉 $Ax=B$를 만족하는 무수히 많다.

위에서와 마찬가지로 $AA^T$를 통해 정방행렬로 만들 수 있다. 이렇게 정방행렬로 만들어준 후, 우리가 최종적으로 원하는 항등행렬을 만들어 보자.

이렇게 $AA^T$를 항등행렬로 만들어 주는 행렬을 left inverse matrix라고 부른다.

💡 4번 경우의 수로 넘어가기 전에, left inverse를 A 오른쪽에, right inverse를 A왼쪽에 놓는다면 어떻게 될까??

바로 우리가 4장에서 배웠던 projection형태가 된다!! 즉 위의 식은 column space에 projection하는 형태이고 아래의 식은 row space에 projection하는 형태이다.

4. r < n, m

4번의 경우가 가장 일반적인 케이스 이다. 예제를 통해 살펴보자.

❓ row space에 존재하는 x 벡터에 행렬 A를 곱하면 Ax는 column space에 존재한다. 또한 마찬가지로 row space에 존재하는 y 벡터에 행렬 A를 곱하면 Ay는 column space에 존재한다. x 와 y는 서로 다른 벡터인데, 과연 Ax와 Ay는 다른 행렬일까??

💡 Proof
만약 Ax 와 Ay가 같다고 가정한다면, $Ax = Ay$ $Ay$를 좌변으로 넘기면, $A(x-y)=0$이 나오게 된다. 식을 통해보면, $x-y$가 null space에 존재해야 한다. 하지만!! x 와 y는 row sapce에 존재하므로 Ax와 Ay는 같지 않음이 증명된다.

How to find (A+)Pseudo inverse

SVD(singular value decompostion)을 사용하면, pseudo inverse를 비교적 쉽게 구할 수 있다. 어떠한 행렬 A를 svd 를 하게되면 다음과 같다.

이제 A를 항등행렬과 최대한 유사하게 만들어 주는 pseudo inverse를 구해보자. 우선 u 와 v는 정방행렬이기 때문에 역행렬을 구할 수 있다. 또한 이들의 역행렬은 전치행렬과 동일하다. 이는 앞장의 SVD정리를 읽어보면 확인할 수 있다. 문제는 m x n 행렬 $\Sigma$이다. 하지만 $\Sigma$는 대각 행렬이기 때문에 최대한 항등행렬에 가깝게 해주는$\Sigma^{+}$는 쉽게 구할 수 있다.

이렇게 SVD를 구하면 u 또는 v는 정방행렬 이기 때문에 pseudo inverse는 모두 $\Sigma$에 따라 결정 되기 때문에 편리하다.