선형대수학

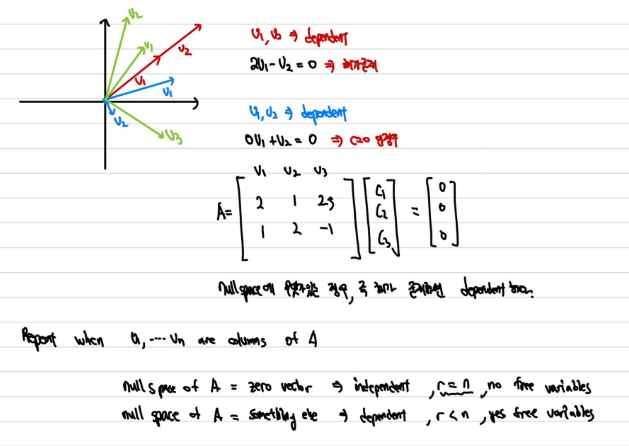
이번 강의의 궁극적이 목표는 어떠한 행렬 A의 rank와 A의 column space의 dimension이 같다는 것을 구하고자 하는 것 이다. Dimension이 무엇인지 다음의 3가지를 통해 이해 해보도록 하자.IndependentSpanBasis벡터들이 Indep

이전 까지 어떠한 행렬 A가 symmetric 하거나 othogonal한 형태일 때의 eigenvalue값을 구하는 방법을 공부하였다. 즉 $A = Q\\Lambda Q^T$ 하지만 SVD를 이용한다면, symmetric하지 않은 행렬도 orthogonal한 행렬들로

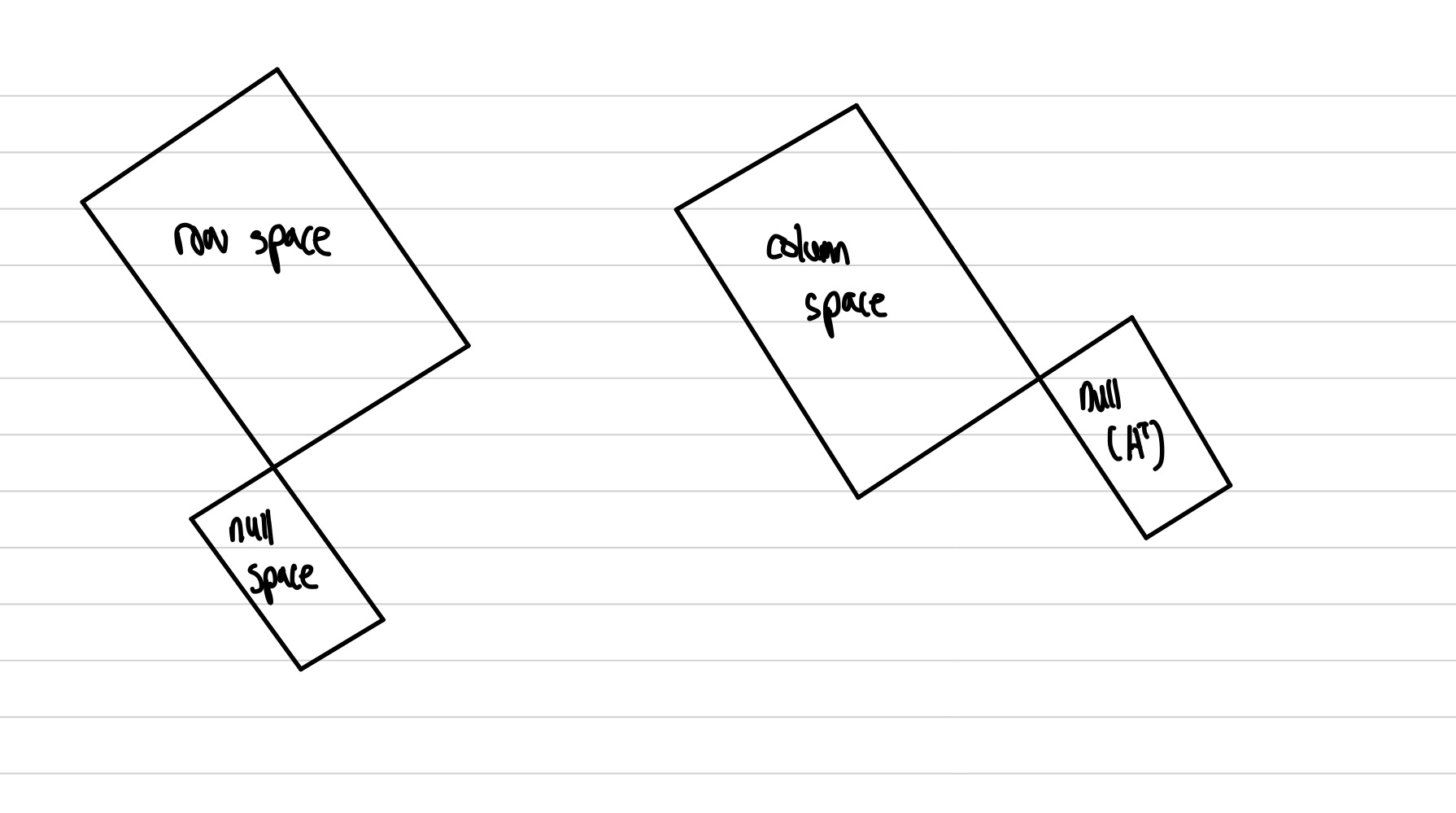
Pseudo inverse가 무엇인지 간단하게 설명하자면, 역행렬은 full rank인 m x m 정방 행렬(square matrix)에서만 정의되는 반면 정방 행렬이 아닌 다른 모양의 행렬에서는 역행렬 대신에 유사 역행렬(pseudo inverse matrix)을 정

이번 강의에서 다룰 내용은 Eigenvalue and Eigenvector이다. 이번 강의에서는 이전 강의에서 배운 Projection 개념과 Determinant 개념이 사용 되기 때문에 이해를 돕기 위해서 이전강의 들을 배우고 듣는 것을 추천한다.어떠한 행렬 Ax는