이 논문은 생성모델계 한 획은 그은 Yang Song이라는 저자가 기존의 DDPM 방식의 diffusion 모델과 Score-based 방식의 diffusion 모델을 하나의 통합된 framework를 제시한 논문이다. 이전에는 노이즈가 추가되는 과정이 discrete한 time으로 표현되었다면, 본 논문에서는 이를 continous한 time으로 풀어나간 논문이다.

1. Introduction

이미지로 부터 노이즈를 생성하는 과정을 쉽다. 하지만 이러한 노이즈로 부터 다시 이미지를 얻어내는 과정은 어렵고 이를 generative modeling이라고 부른다. 기존의 딥러닝 기반 방법론은 크게 2가지로 나눌 수 있다.

1. SMLD/NCSN
   여러 가우시안으로 데이터를 단계적으로 교란하고, 각 단계의 스코어를 학습해 Langevin Monte-Carlo-Markov-Chain을 통해 점진적으로 깨끗한 이미지를 얻어낼 수 있다.

2. DDPM
   여러 가우시안을 누적해 데이터를 노이즈하게 만들고, 역 Markov chain을 통해서 점진적으로 깨끗한 이미지를 얻어낼 수 있다.

이 두가지 방법에 대해서는 아래의 Background 파트에서 자세하게 다루고 있다. 이러한 두 방식 모우 노이즈를 넣었다, 제거해나가며 socre를 학습하고 이를 통해 데이터 분포 $p(x)$로 부터 깨끗한 이미지를 sampling할 수 있다는 점에서 공통점을 가지고 있다고 판단해 이 두 방식을 SDE 관점에서 통합하여 표현하였다.

본 논문에서는 Stochastic differential equation(SDE)을 통해 복잡한 데이터분포 $p(x)$로부터 우리가 알고있는 prior distribution(표준 정규분포)로 보내는 과정을 처리하고,

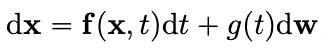
대응되는 reverse-time SDE를 통해 prior distribution에서 데이터분포 $p(x)$로 변환하는 과정을 제안하였다.

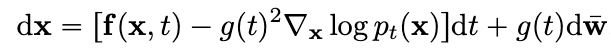
이렇게 새롬게 제안한 SDE 방식의 score-based diffusion model은 아래의 3가지 contribution으로 정리할 수 있다.

1. Flexible sampling and likelihood computation
   sampling을 하는 reverse-time SDE로 임의의 SDE-solver를 사용할 수 있다. 또한 본 논문에서는 일반적으로 사용되지 않는 특별한 2가지 형태의 SDE-solver도 제안하였다.
   1. Predictor-Corrector samplers
   2. Deterministic samplers
   

2. Controllable generation
   Conditional reverse-time SDE가 uncoditional score로부터 추정할 수 있기 때문에 추가적인 학습 없이 class-conditional generation, image inpainting, colorization등 다양한 inverse problem이 가능하다.

3. Unified framework
   앞서 말했던 SMLD, DDPM을 통합된 SDE 관점에서 해석하였다.

2. Background

2.1 SMLD

깨끗한 이미지 $x$가 주어졌을 때, 노이즈가 낀 $\tilde{x}$를 표현하면 다음과 같이 표현할 수 있다.

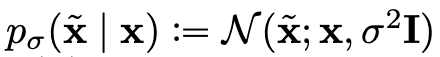
그렇다면 노이즈가 낀 이미지 $\tilde{x}$의 확률분포는 다음과 같이 표현할 수 있다. 여기서 $p_{data}(x)$는 데이터의 분포를 뜻하게 된다.

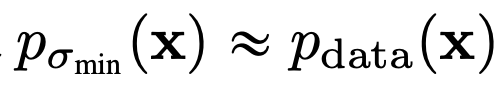
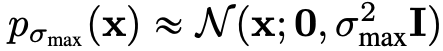
그래서 이러한 노이즈 스케쥴링을 따르는 네트워크는 다음과 같은 방법으로 noisy한 이미지와 noisy step이 주어졌을 때, score를 예측하며 데이터 분포 $p_{data}(x)$를 학습할 수 있다고 주장한다.

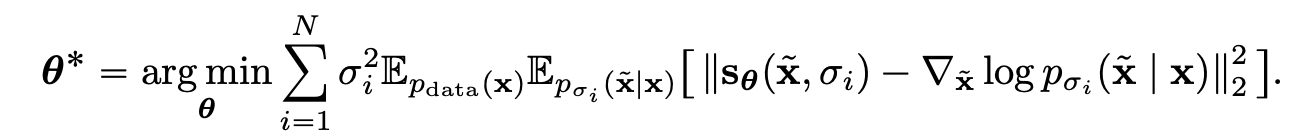
이렇게 네트워크가 잘 학습되고 난 뒤, score로 부터 깨끗한 이미지로 복원해 내는 과정은 Langevian Monte-Carlo-Markov-Chain를 M step에 걸쳐 순차적으로 진행된다.

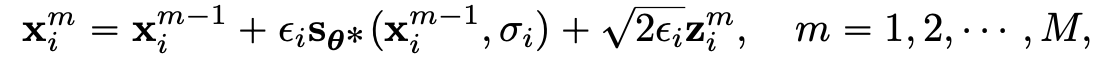
이렇게 M번 step 이 반복된다면 $x_1^M$ 은 다음과 같은 분포로 부터 샘플링 되었다고 할 수 있다.

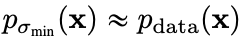
즉 우리가 원하는 $p_{data}(x)$ 로부터 $x$를 샘플링할 수 있게 된 것 이다.

2.2 DDPM

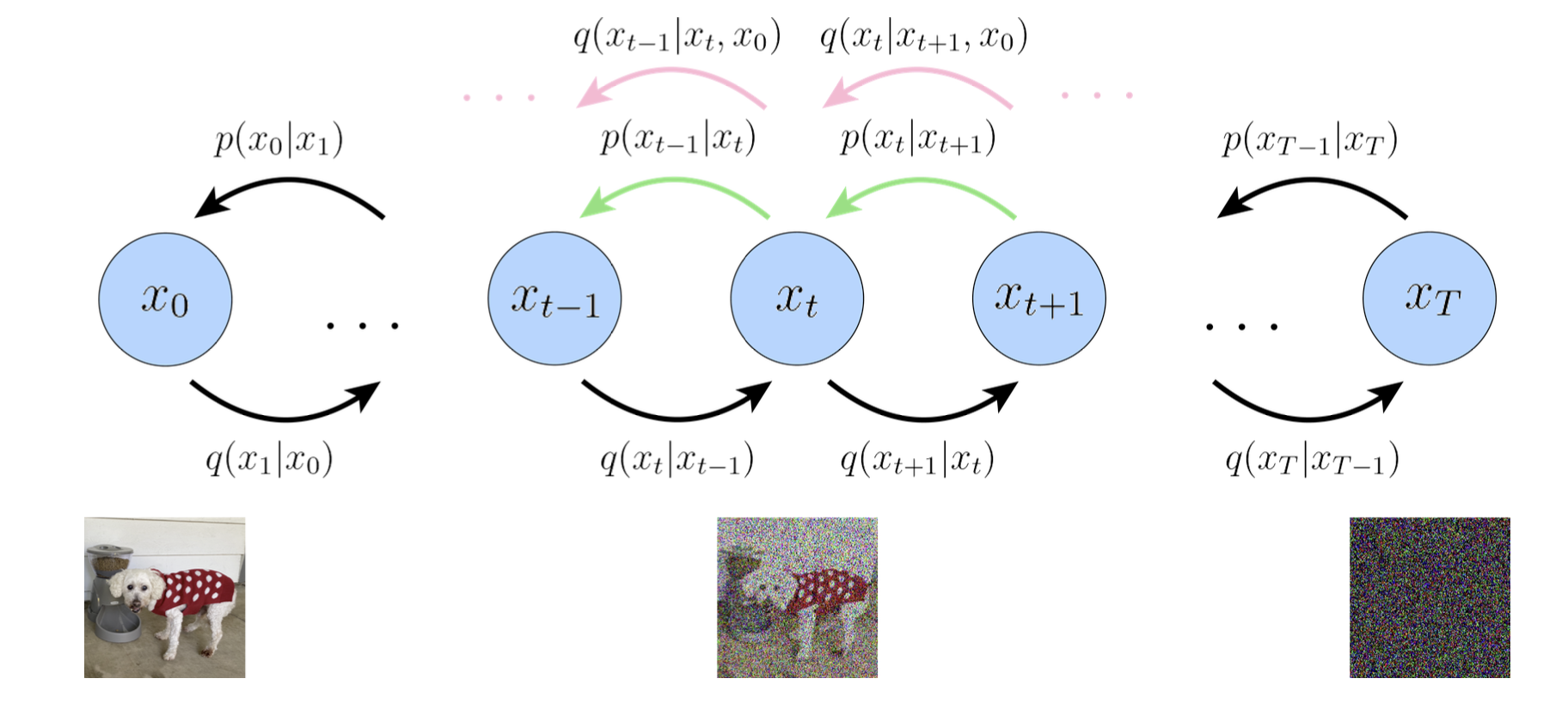
DDPM의 노이지한 이미지는 다음과 같이 표현할 수 있다.

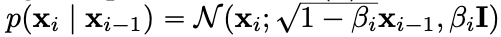
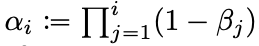
최종적으로 pertubed data distribution은 SMLD와 비슷하게 다음과 같이 표현할 수 있다.

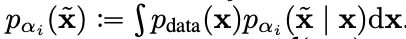
DDPM에서는 네트워크가 ELBO를 최대한으로 키우는 과정을 통해서 학습을 한다. 약간의 텀 조정을 통해서 다음과 같이 score function을 학습할 수 있다.

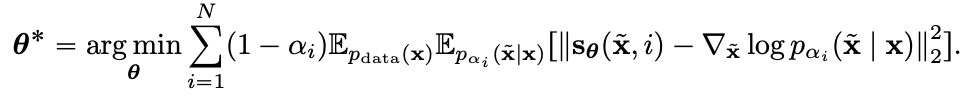
DDPM에서는 노이즈한 데이터를 정의하던 markov chaing 형식을 거꾸로 진행하며 샘플링을 진행한다. 이러한 방식을 ancestral sampling이라고 부른다.

3. Score-based generative modeling with SDEs

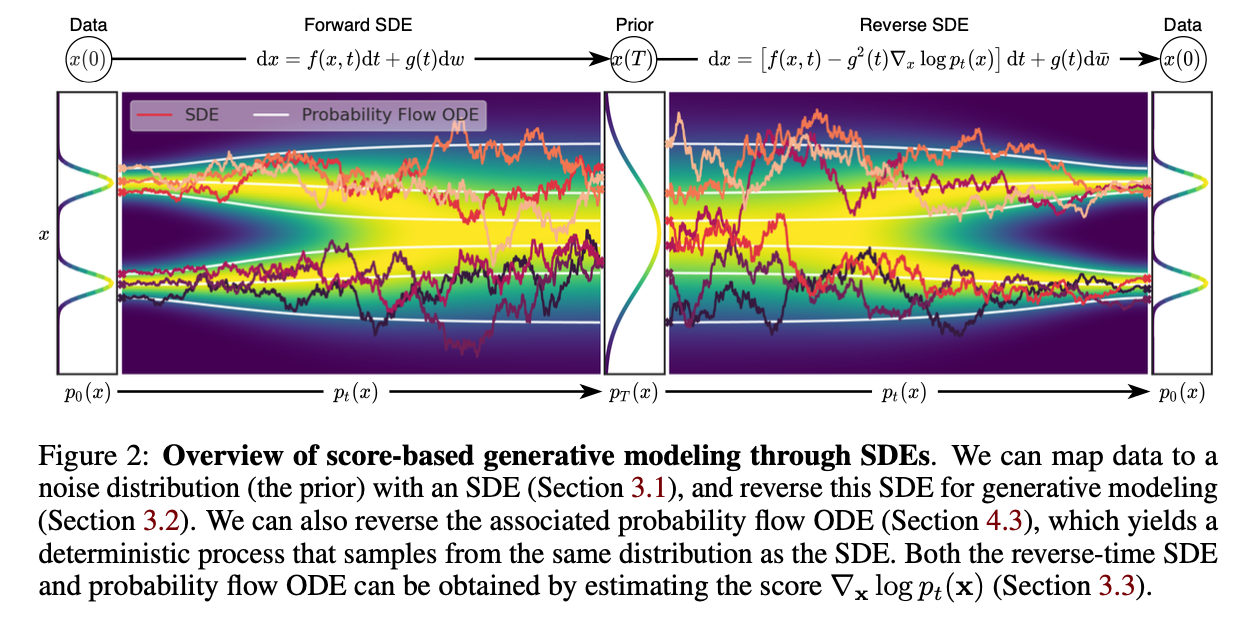
위에서 말한 SMLD와 DDPM 모두 잘 작동할 수 있었던 이유는 바로데이터에 노이즈를 추가함으로써 깨끗한 원본 이미지에 혼란을 주는 방식을 사용한 것이다. 따라서 본 논문에서는 이러한 방식을 그대로 사용하되, 이렇게 데이터에 노이즈를 추가하는 방식을 descrete한 단계가 아닌, continuos하게 표현하는 SDE로 정의하여 일반화 시켰다.

3.1 Perturbing data with SDEs

forward과정 즉 노이즈를 추가하는 과정은 다음과 같이 정의한다.

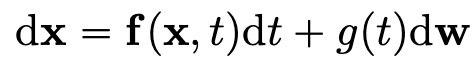
이 식은 $t$ 에서 $t+1$로 갈때, 이미지 $x(t)$가 얼만큼 변화되는지를 표현한 식이다. $w$는 winer process (Brownian motion이라고 부르기도 한다.)를 뜻하고 $g(t)$는 diffusion coeficient로 하나의 상수이다. $f(t)$는 drift coefficinet라고 부르며 $t$와 $x$를 입력으로 받아 하나의 벡터를 내뿜는 함수이다.

3.2 Generating samples by reversing the SDE

이제 우리가 알고있는 prior distribution으로 부터 깨끗한 이미지를 얻어내는 과정을 sampling이라고 하는데 이 sampling은 아주 간단하게 reverse-time SDE를 통해 정의가 가능하다.

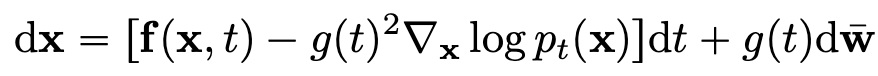
3.3 Estimating scores for the SDE

sampling 식을 살펴보면 score를 알아야, 원래의 깨끗한 데이터 $x(0)$로 돌아갈 수 있는 걸 확인할 수 있다. 따라서 score-based Neural Network는 다음과 같이 학습하게 된다.

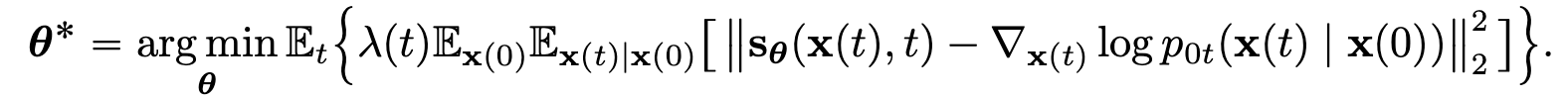
3.4 VE,VP SDEs and beyond

그렇다면 SMLD와 DDPM에서는 SDE로 어떻게 표현할 수 있을까? 즉 SMLD와 DDPM 에서의 $f(x,t)$랑 $g(t)$를 다음과 같이 구할 수 있다.

3.4.1 SMLD SDE

원래 기존의 forward과정은 다음과 같다.

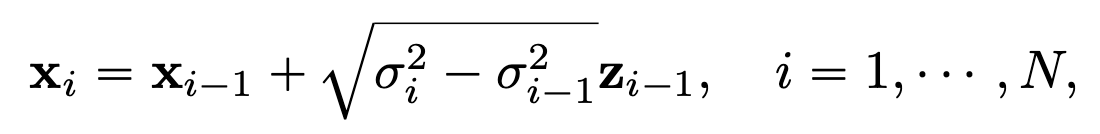
이를 SDE로 다시 표현하면 다음과 같다.

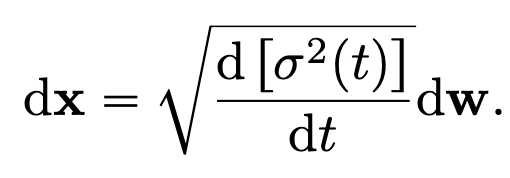
이러한 형식을 Variance exploding 이라고 부른다.

3.4.2 DDPM SDE

DDPM에서의 forward 과정은 다음과 같다.

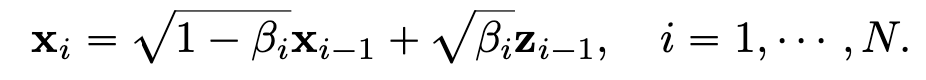
이를 SDE로 다시 표현하면 다음과 같다.

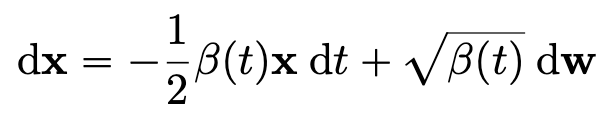
3.4.3 sub-VP SDE

본 논문에서는 새로운 SDE를 제시하는데 variance가 preserving 되지만 기존의 VP 보다 조금더 작은 분산을 가지게 함으로써 성능을 높였다고 한다.

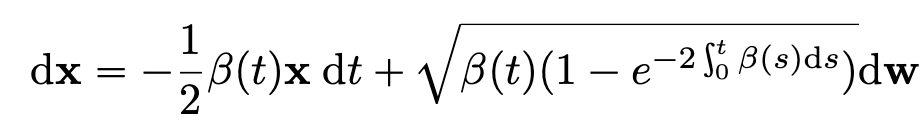
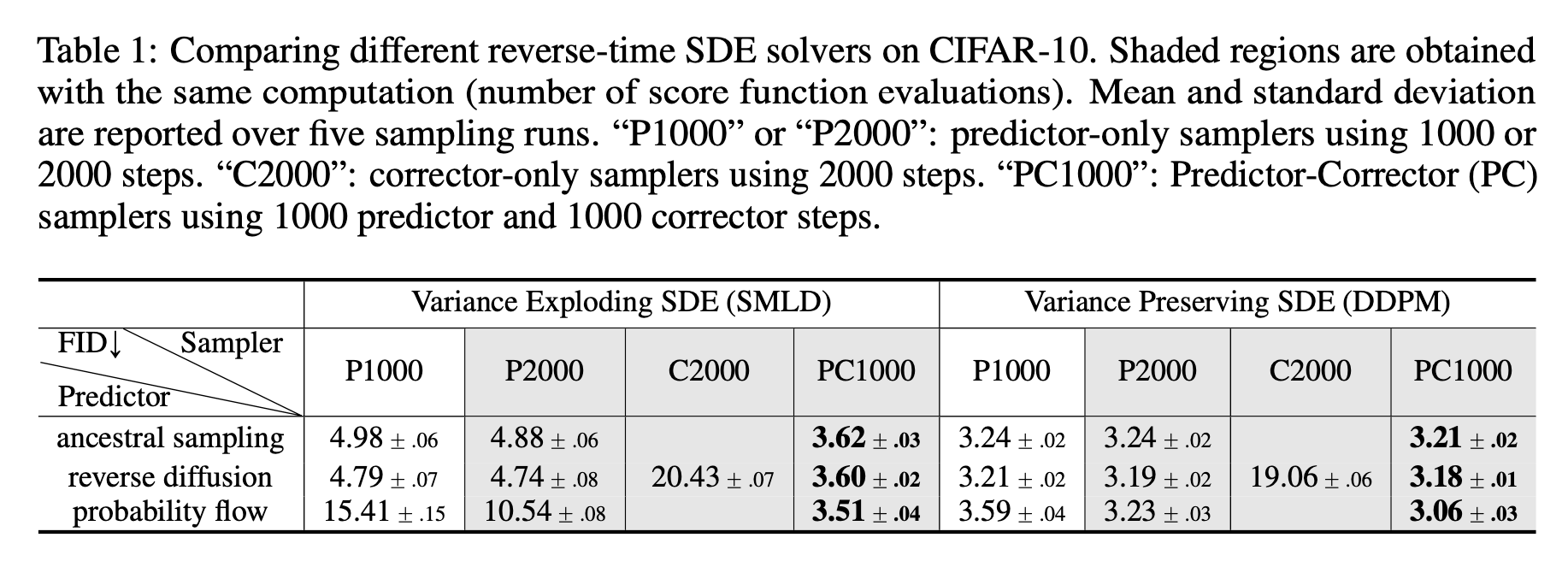
4. Solving the reverse-time SDE

깨끗한 데이터 $x_0$를 뽑을 수 있는 데이터 분포 $p(x)$를 학습한 네트워크가 있다면 이제 이 score를 바탕으로 sampling을 진행해야 하는데 위에서 볼 수 있듯이 sampling을 위해서는 reverse-time SDE를 풀어야 한다. 아래의 그림은 다양한 sampler를 활용하여 실험을 진행한 결과이다.