Dimension

이번 강의의 궁극적이 목표는 어떠한 행렬 A의 rank와 A의 column space의 dimension이 같다는 것을 구하고자 하는 것 이다. Dimension이 무엇인지 다음의 3가지를 통해 이해 해보도록 하자.

• Independent
• Span
• Basis

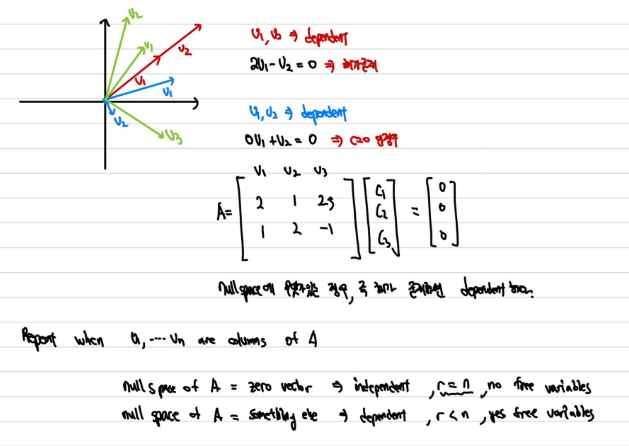
Independent

벡터들이 Independent 한지 dependent 한지는 다음의 조건을 통해 확인 할 수 있다.

c1x_1 + c_2x_2 + ... + c_nx_n = 0의 해가 모든 c가 0인 경우밖에 존재하지 않는다면, _x벡터들은 independent 하다.

즉 A의 영공간이 zero vector 뿐이라면 벡터들은 independent하고, zero가 아닌 다른 값들로 이루어져 있다면 벡터들은 dependent하다.

• examples

Spanning

span이라는 뜻이 무엇일까? 다음의 조건을 통해 확인할 수 있다.

만약 어떠한 벡터공간 V가 w1,w_2, ... , w_n의 linear combination으로 이루어져 있다면 이 벡터들은 벡터공간 V를 spa_n 한다고 한다.

• example

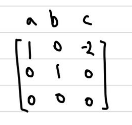
a,b,c 벡터들은 2차원의 평면을 span한다. 하지만 a와 b만 있어도 2차원 공간을 span할 수 있다. 또한 a와 c만 있다면 x축 만을 span하게 된다.

Basis

어떠한 행렬 V의 Basis는 다음과 같이 정의 된다.

다음의 두 가지 조건을 만족해야 한다.

1. 벡터들이 independent 하다.
2. 벡터들이 V를 span 해야 한다.

• example

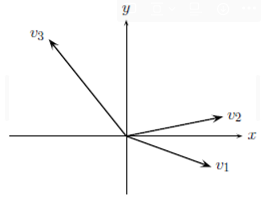
위의 예시는 2차원 평면이다. 이 예시에서 basis는 어떠한 벡터가 올 수 있을까? 만약 한개의 벡터만 존재하게 된다면, independent하다는 조건은 만족하지만 2차원 공간을 span하지는 못한다. 만약 3개의 벡터들을 basis로 정하게 된다면 2차원 공간을 span할 수 있지만 dependent하기 때문에 basis가 될 수 없다. 즉, 2차원 공간에서는 2개의 벡터가 basis가 될 수 있다. 다시 말해 어떠한 공간의 basis개수는 vector의 개수와 동일하다는 것을 알 수 있다.

이제 dimension의 정의를 확인해 보자.

Dimension = basis 벡터들의 개수

이를 다른 방식으로 작성해보면,

rank(A) = number of pivot columns = dimension of column space of A 이라는 결과가 나오게 된다.