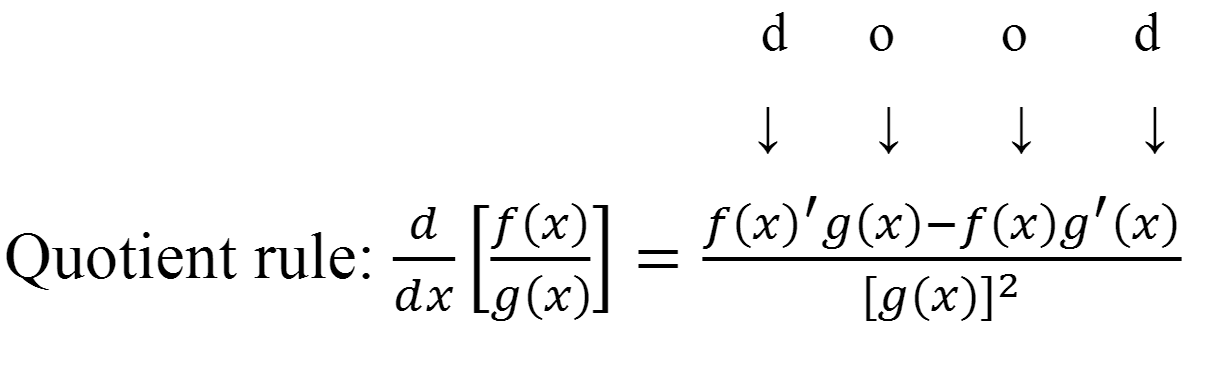1. 개요
다중 분류를 위한 인공신경망을 빌드할 때 보통 마지막 레이어의 출력값에 Softmax를 직용시키고 실제 레이블값과 비교하여 Cross-Entropy Loss를 계산한다. Softmax를 통해 마지막 레이어의 출력값을 확률값으로 변환할 수 있고 Cross-Entropy를 통해 실제 분포와 확률값이 얼마나 차이나는지 측정할 수 있기 때문이다.
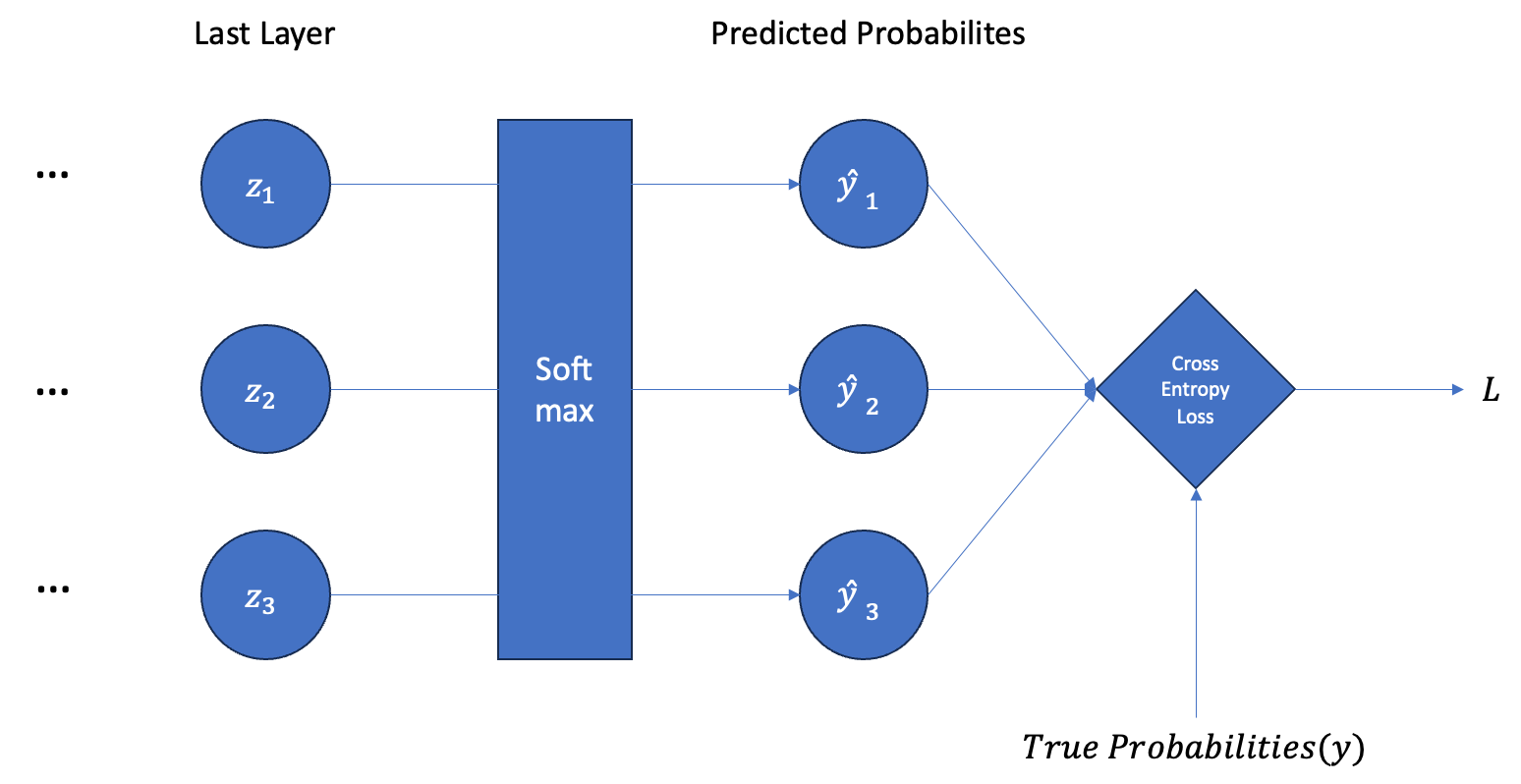
따라서 Softmax와 Cross-Entropy를 세트로 묶어서 보기도 한다. Softmax를 적용하고 Cross-Entropy를 통해 손실값의 신경망의 마지막 출력값 zi에 대한 미분값은 다음과 같이 표현된다. 이러한 공식이 어떻게 도출되었는지 차례대로 확인해보자.
∂z∂L=y^−y
2. Softmax의 미분
Softmax의 수식은 다음과 같다. i번째 클래스에 대한 확률의 예측값은 다음과 같이 계산된다.
y^i=j=1∑cezjezi
이를 zi에 대해서 미분해보자. 몫 규칙(quotient rule)에 의해 우선 다음과 같이 미분할 수 있다. ex를 x에 대해 미분하면 그대로 ex인 것도 참고하자.
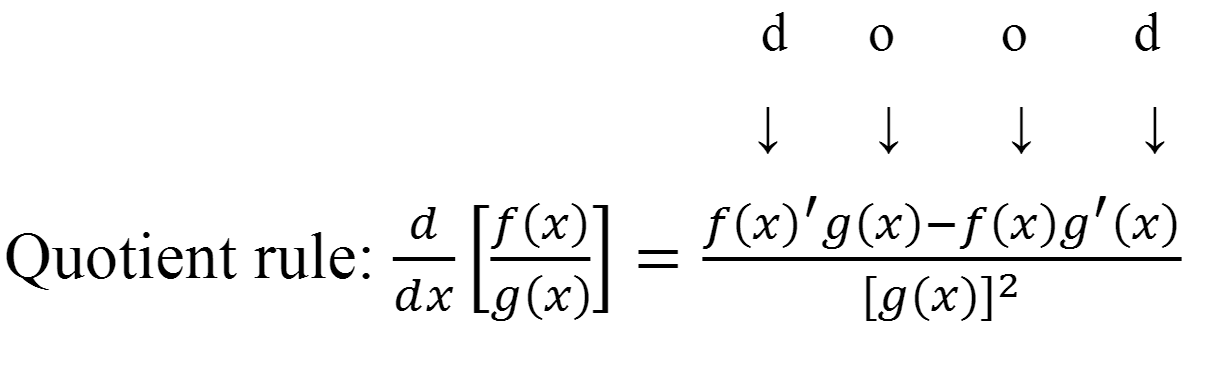
∂zi∂y^i=(j=1∑cezj)2ezi∗j=1∑cezj−(ezi)2
위의 식은 아래와 같이 전개할 수 있다.
∂zi∂y^i=j=1∑cezjezi∗j=1∑cezjj=1∑cezj−ezi
y^i=j=1∑nezjezi 이므로 이는 결국 다음과 동일하다.
∂zi∂y^i=y^i∗(1−y^i)
하지만 y^의 인덱스와 z의 인덱스(i)가 서로 다르다면 미분값은 달라진다. zi 값은 zn에 의존하지 않으므로 다음과 같이 미분된다.
∂zn∂y^i=(j=1∑cezj)20∗j=1∑cezj−ezi∗ezn
∂zn∂y^i=−(j=1∑cezj)2ezi∗ezn
∂zn∂y^i=−j=1∑cezjezi∗j=1∑cezjezn
∂zn∂y^i=−y^i∗y^n
따라서 다음과 같이 정리할 수 있다.
∂zn∂y^i={y^i∗(1−y^i)(i=n)−y^i∗y^n(i=n)
3. Cross-Entropy의 미분
Cross-Entropy Loss의 수식은 다음과 같다.
L=−i=1∑cyi∗log(y^i)
이를 차례대로 zn에 대해 미분해보자. yi는 상수이고 ∑는 zn에 의존하지 않으므로 무시할 수 있다.
∂zn∂L=−i=1∑cyi∗∂zn∂log(y^i)
연쇄 법칙에 의해 다음과 같이 전개할 수 있다.
∂zn∂L=−i=1∑cyi∗∂y^i∂log(y^i)∗∂zn∂y^i
log(x)의 미분은 x1와 같다.
∂zn∂L=−i=1∑cyi∗y^i1∗∂zn∂y^i=−i=1∑cy^iyi∗∂zn∂y^i
∂zn∂y^i은 Softmax의 미분과 동일하다. 따라서 i=n인 경우와 i=n인 경우로 나누어서 생각할 수 있다.
∂zn∂L=−y^nyn∗y^n∗(1−y^n)+i=n∑cy^iyi∗y^i∗y^n
식을 정리하면 다음과 같다.
∂zn∂L=−yn+yn∗y^n+i=n∑cyi∗y^n
∂zn∂L=−yn+i=1∑cyi∗y^n
y는 원-핫 인코딩 벡터이므로 yi 중 하나만 1의 값을 가진다. 따라서 다음과 같이 정리된다.
∂zn∂L=−yn+y^n=y^n−yn
따라서 ∂z∂L이 y^−y임을 증명할 수 있다.