Word2Vec

김회정·2023년 7월 3일

머신러닝

목록 보기

2/7

1. 분포 가설

단어를 컴퓨터가 이해할 수 있는 벡터로 표현하기 위해서는 통계 기반 기법 또는 추론 기반 기법을 사용할 수 있다. 통계 기반 기법은 동시 등장 행렬(Co-occurrence Matrix)과 같은 방법이 있고 추론 기반 기법에는 오늘 소개하고자 하는 Word2Vec이 있다.

통계 기반 기법과 추론 기반 기법은 공통적으로 분포 가설을 따르고 있다. 분포 가설은 단어의 의미는 주변 단어에 의해서 결정된다는 것을 가정하고 있다. 그렇기 때문에 기준 단어의 context size 내에서 동시에 등장하는 단어는 기준 단어의 의미를 형성한다고 말할 수 있다. 따라서 두 기법 모두 단어의 동시발생 가능성을 모델링하는 것을 목표로하고 있다.

2. 통계 기반 기법의 문제점

통계 기반 기법은 코퍼스 전체의 통계를 이용해 1회의 처리로 단어의 분산 표현을 얻는다. 보통 전체 코퍼스를 통해 동시 등장 행렬을 계산하고, 계산된 동시 등장 행렬에 SVD(Singular Value Decomposition)을 통해 단어에 대한 밀집 표현(Dense Representation)을 생성한다. 하지만 이와 같은 방식은 상당한 컴퓨터 자원을 들여 장시간 계산해야 하는 불편함이 있다.

이에 반해 추론 기반 기법은 학습 데이터의 일부를 사용하여 순차적으로 학습한다(Mini-Batch Training). 따라서 데이터를 작게 나눠서 학습하기 때문에 코퍼스 내의 어휘가 많아 계산량이 큰 작업을 처리하기 어려운 경우에도 신경망을 학습시킬 수 있다는 장점이 있다.

3. Word2Vec

Word2Vec은 말 그대로 단어를 단어(word)를 벡터(vector)로 표현하는 방법이다. 단어를 벡터로 표현하기 위해 신경망을 이용해 추론을 수행하는데, 추론 방법에는 크게 두 가지 방법이 있다.

3.1 CBOW(Continous Bag of Words)

CBOW 추론 방법은 주변 단어(context)를 바탕으로 중앙 단어(target)을 예측하는 방법이다. 따라서 모델의 입력은 주변 단어이며 모델이 추론할 대상은 중간에 위치한 단어이다.

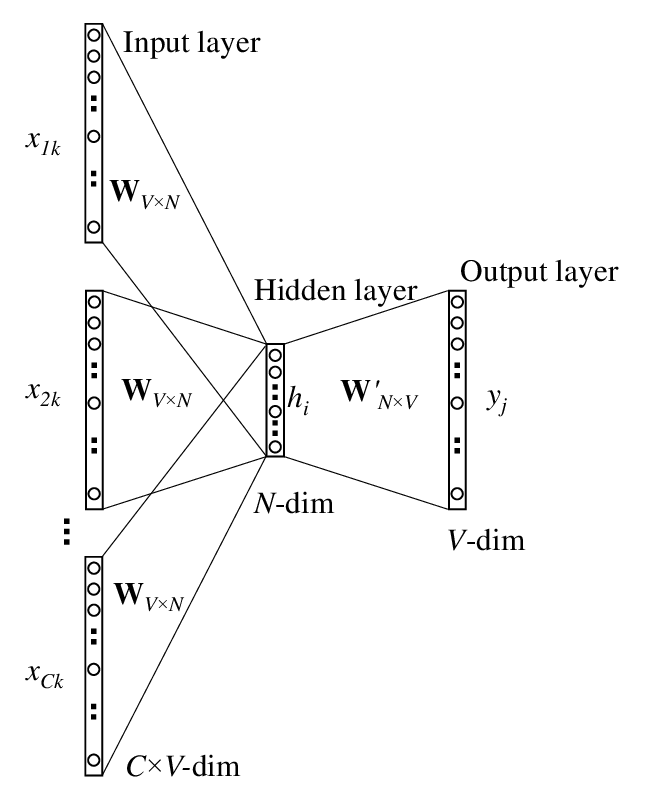
과정은 다음과 같다.

주변 단어의 원-핫 인코딩을 를 행렬 연산을 통해 밀집 표현으로 변환한다.
각 단어의 밀집 표현의 평균 값을 구한다.
구한 평균 값에 다시 행렬 연산을 적용해 중앙에 올 단어에 대한 점수(score)를 구한다.

입력층의 변환을 담당하는 가중치의 사이즈는 (vocab_size, hidden_size)이며, 출력층의 변환을 담당하는 가중치의 사이즈는 (hidden_size, vocab_size)이다.

3.2 Skip-Gram

skip-gram은 CBOW와 반대로 중앙 단어를 이용해 주변 단어를 추론하는 방법이다.

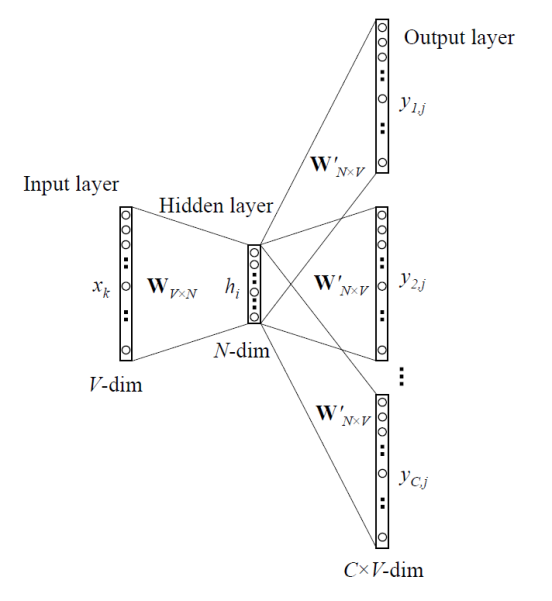
3.3 CBOW와 skip-gram의 성능 비교

단도직입적으로 skip-gram 방식으로 생성된 단어 분산 표현의 정밀도가 CBOW 방식으로 생성된 단어 분산 표현의 정밀도보다 높다. 특히 코퍼스 사이즈가 커질 수록 저빈도 단어나 유추 문제의 성능 면에서 skip-gram 모델이 더 뛰어난 경향이 있다.

성능 차이에 대한 직관적인 생각은 skip-gram의 유추 과정이 더 어렵기 때문이다. CBOW는 문맥을 가지고 하나의 중앙 단어를 추론하면 되지만, skip-gram은 하나의 중앙 단어를 가지고 모든 문맥의 단어를 추론해야한다는 점에서 난이도에 차이가 있다. 따라서 skip-gram이 더욱 어려운 문제를 통해 훈련되는 만큼 단어의 분산 표현을 보다 잘 표현할 수 있을 것이라 생각할 수 있다.

반면, 학습 속도 면에서는 CBOW 모델이 더 빠르다. skip-gram 모델은 손실을 맥락(context)의 사이즈만큼 구해야 하기 때문에 계산 비용이 그만큼 커지기 때문이다.

4. 확률적 표현

CBOW 방식을 확률적 표현으로 나타내보자. CBOW 기반 모델은 맥락을 입력받았을 때 중앙에 나타날 단어의 확률들에 대해서 출력하는 것이다. 맥락의 윈도우 사이즈가 1이고, 맥락 $W_{t-1}, W_{t+1}$ 이 주어졌을 때 중앙 단어 $W_{t}$ 에 대한 확률은 다음과 같이 표현할 수 있다.

P(W_{t}|W_{t-1},W_{t+1})

이를 이용해서 CBOW 모델의 손실 함수도 간결하게 표현할 수 있다. 확률 분포 차이에 대한 오차를 구하기 위해 Cross-Entropy 손실 함수를 사용하는 데 손실 함수에 대한 수식은 다음과 같다.

L=-\sum\limits_kt_{k}*log(y_{k})

$t_{k}$ 는 정답 레이블이며 원핫 벡터로 표현된다. 여기서 문제에 대한 정답은 $W_{t}$ 이므로 $W_{t}$ 에 해당하는 원소만 1이고 나머지는 0이다. 해당 사항을 감안하면 다음 식을 유도할 수 있다.

L=-logP(W_{t}|W_{t-1},W_{t+1})

따라서 CBOW 모델의 손실 함수는 단순히 해당하는 단어의 확률에 log를 취한 다음 마이너스를 붙인 것과 같다. CBOW 모델의 학습이 수행하는 일은 해당 손실 값을 최대한 작게 만드는 것이다. 해당 과정에서 업데이트된 모델의 가중치가 단어의 분산 표현인 것이다.

반면 skip-gram은 하나의 입력으로 맥락으로 올 단어들의 확률들에 대해 예측하는 것이므로 다음과 같이 표현할 수 있다.

P(W_{t-1},W_{t+1}|W_{t})

맥락으로 오는 단어들 사이에 조건부 독립(Conditional Independence)를 가정하면 다음과 같이 표현할 수 있다.

P(W_{t-1},W_{t+1}|W_{t})=P(W_{t-1}|W_{t})*P(W_{t+1}|W_{t})

이에 대한 Cross-Entropy 손실을 구하면 다음과 같다.

L=-logP(W_{t-1},W_{t+1}|W_{t})=-logP(W_{t-1}|W_{t})P(W_{t+1}|W_{t})=-(logP(W_{t-1}|W_{t})+logP(W_{t+1}|W_{t}))

5. word2vec의 가중치와 분산 표현

추론 작업에 대해 훈련된 Word2Vec 모델의 가중치는 단어에 해당하는 분산 표현의 look-up table이라고 이해할 수 있다. 입력으로 들어오는 단어는 원-핫 벡터 형태이기 때문에 입력과 가중치의 행렬곱은 사실상 look-up table에서 단어의 인덱스와 일치하는 분산 표현을 찾는 것과 같다.

입력(단어)를 밀집 표현으로 변환하는 가중치와 밀집 표현을 다시 출력(단어)으로 변환하는 가중치 모두 분산 표현의 look-up table로 사용할 수 있지만 보통 word2vec에서는 입력 측의 가중치를 이용한다.