sigmoid 함수의 미분

1. 정의

sigmoid 함수는 s자 형태의 함수이다. sigmoid 함수의 치역은 (0, 1)이다. 즉, 입력된 값을 0과 1 사이의 값으로 변환시켜준다는 의미이다. non-linearity를 부여하기 위해 sigmoid 함수를 사용한다.

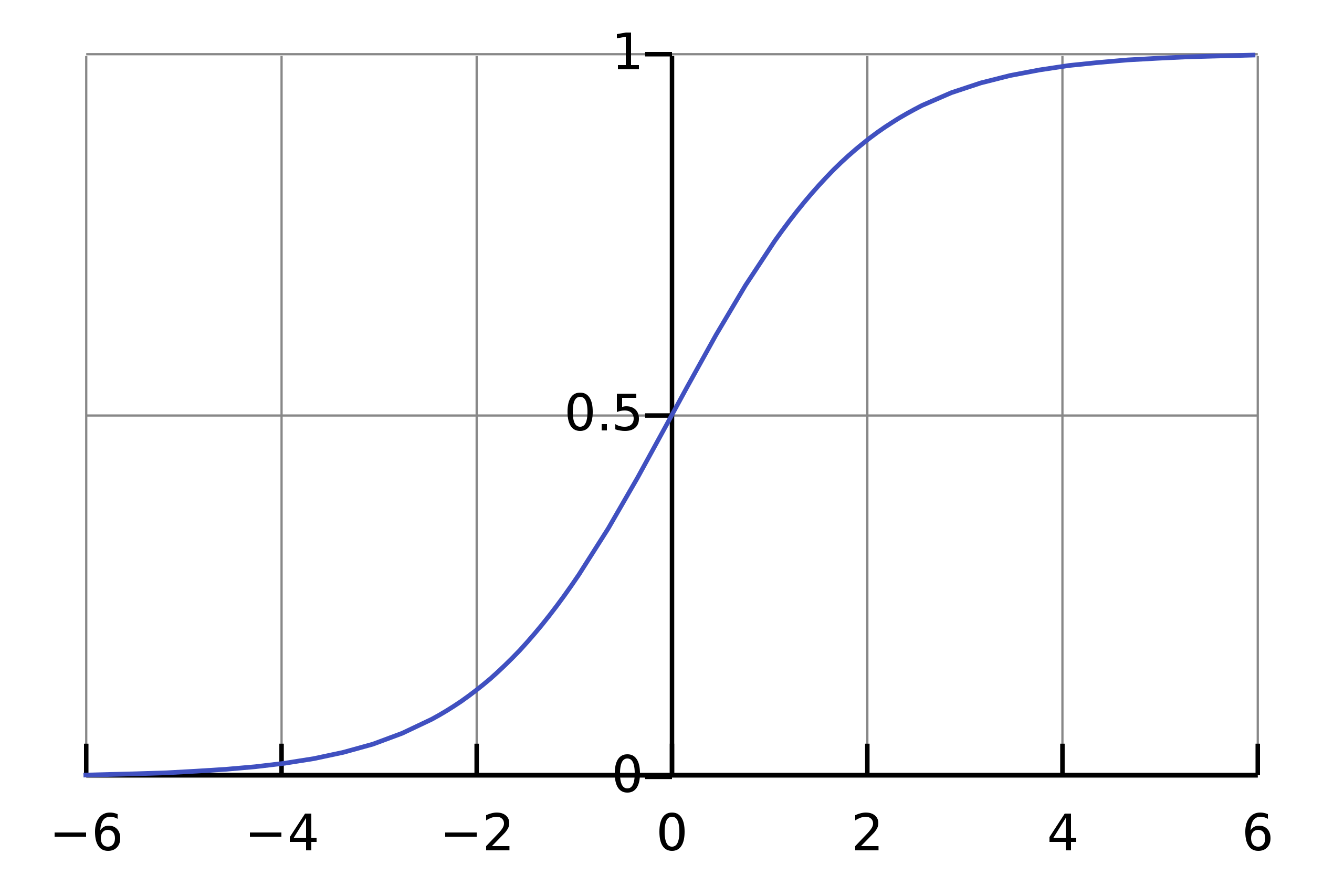
2. sigmoid 함수의 미분

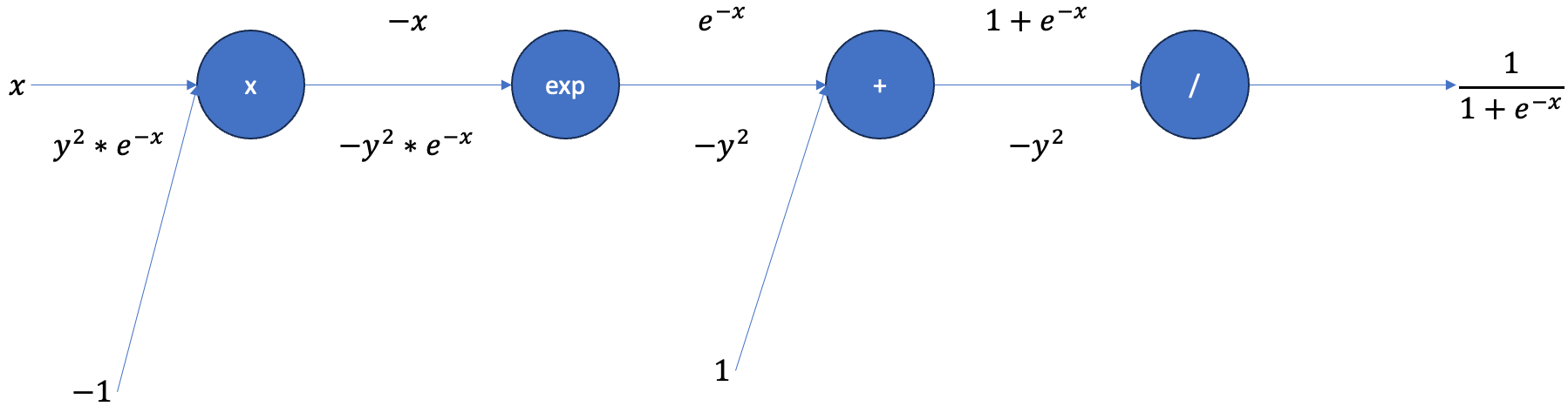
우선 sigmoid 함수의 전체 계산 그래프를 살펴보면 다음과 같다. 계산 그래프에 따라서 마지막 연산부터 차례대로 미분을 해보자.

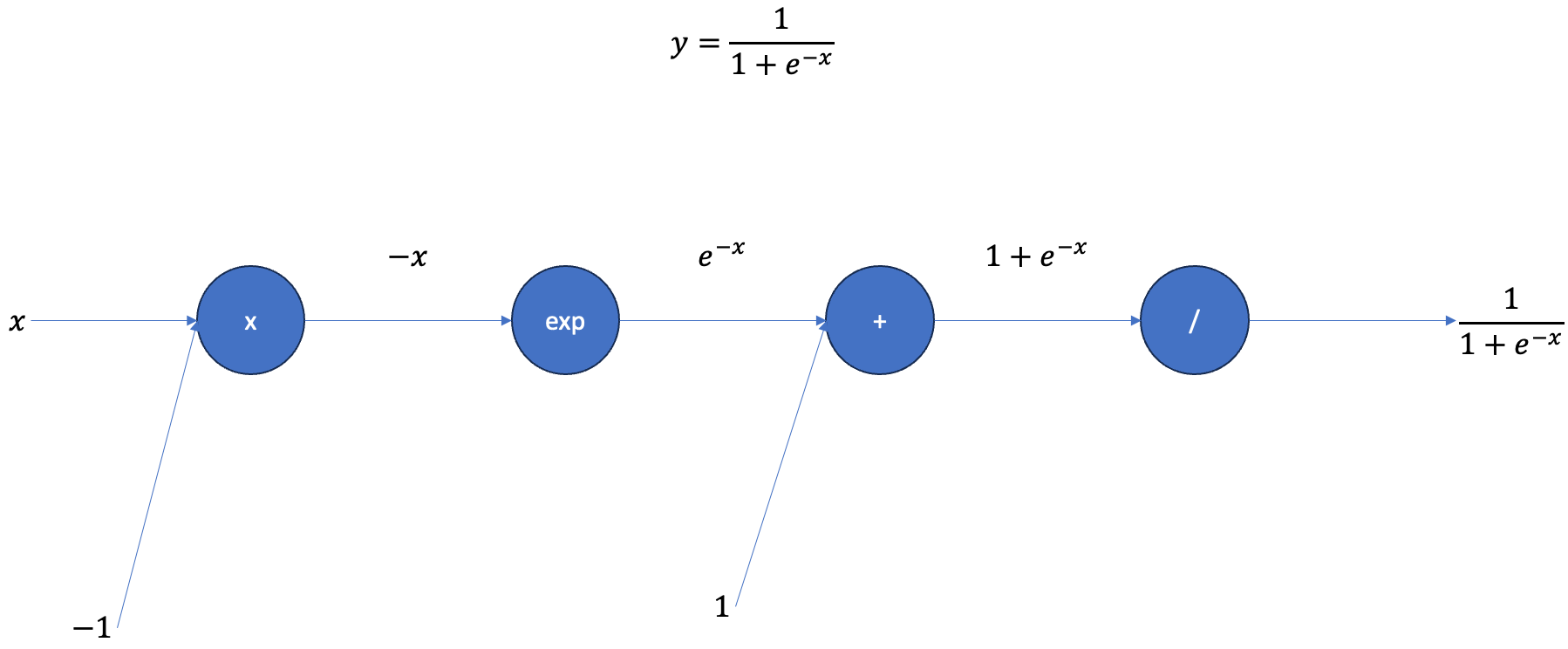
마지막 연산은 $y={1 \over x}$와 같다. ${1 \over x}=x^{-1}$이므로 미분하면 $-x^{-2}$으로 표현할 수 있다. 이는 $-y^{2}$와 동일하다.

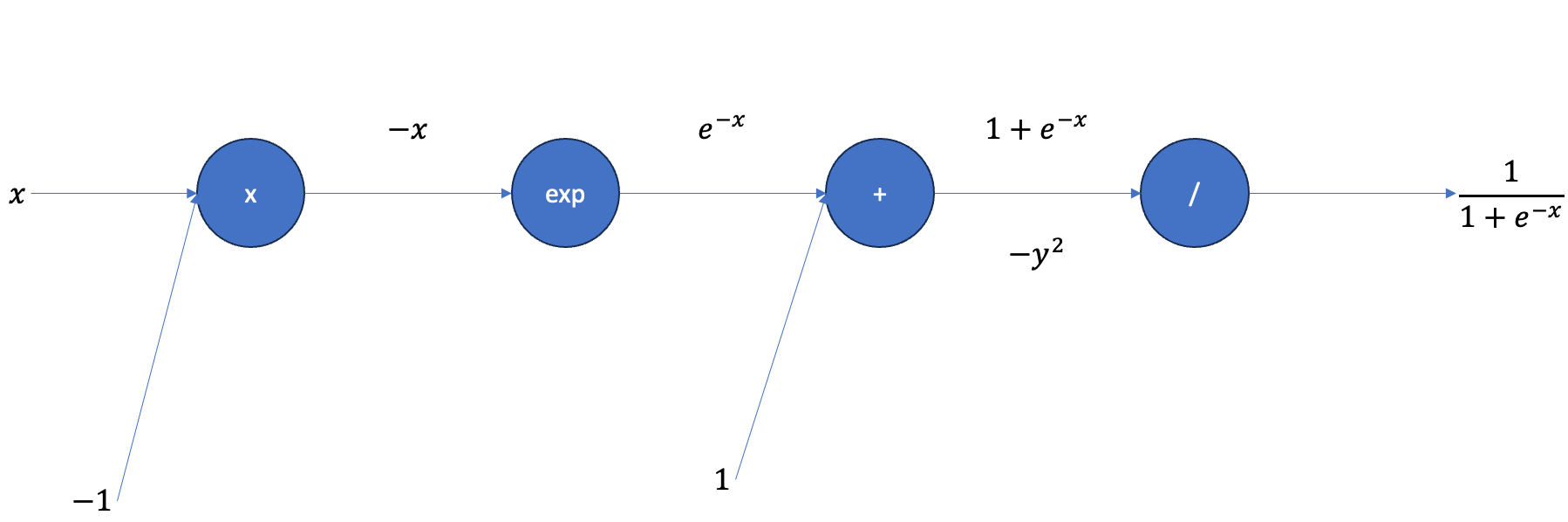
더하기 연산은 미분값을 바로 이전 연산으로 흘릴 수 있다. 지수함수 $e^{x}$의 미분값은 그대로 $e^{x}$이므로 그대로 곱해줄 수 있다.

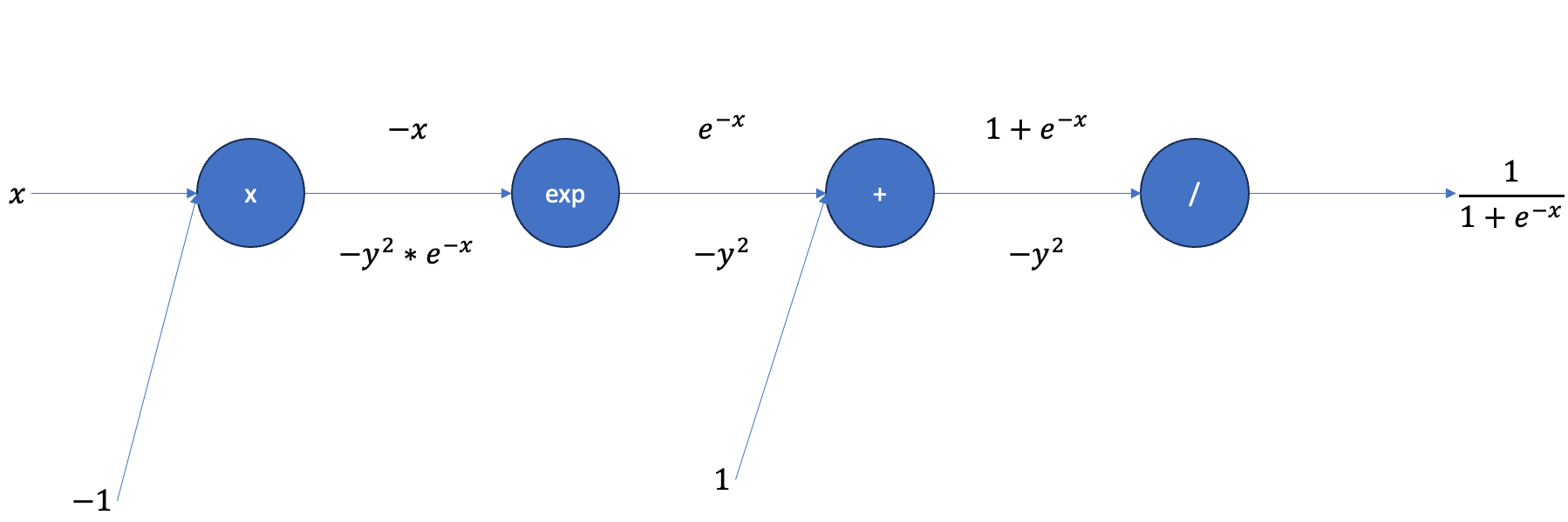
$-x$를 미분하면 $-1$이므로 이를 곱해주면 최종적으로 $y$를 $x$에 대해 미분한 값은 $y^{2}*e^{-x}$이다.

$y는 {1 \over 1+e^{-x}}$이므로 $y^{2}*e^{-x}={e^{-x} \over (1+e^{-x})^{2}}$이다. 이는 ${1 \over (1+e^{-x})}*{e^{-x} \over (1+e^{-x})}$로 표현할 수 있고, 결국 $y*(1-y)와 동일하다.$

따라서 sigmoid 함수 $y={1 \over 1+e^{-x}}$의 미분값은 $y*(1-y)$이다.