Cross-Entropy Loss Function

이 글은 다음 글을 정리한 글입니다.
https://towardsdatascience.com/cross-entropy-loss-function-f38c4ec8643e

1. Entropy

랜덤 변수 X의 엔트로피는 가능한 결과 변수에 내재된 불확실성의 정도이다.

$p(x)$를 랜덤 변수 $X$의 확률 분포(Probability Distributiom)이라고 할 때, 엔트로피는 다음과 같이 정의될 수 있다.

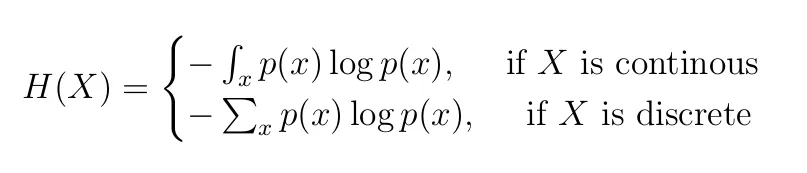
음수 부호가 붙은 이유는 로그함수의 그래프를 생각해보면 쉽게 이해할 수 있다. 확률값은 0과 1 사이의 값을 가지므로 $log(p(x))$는 음수의 값을 가지기 때문이다.

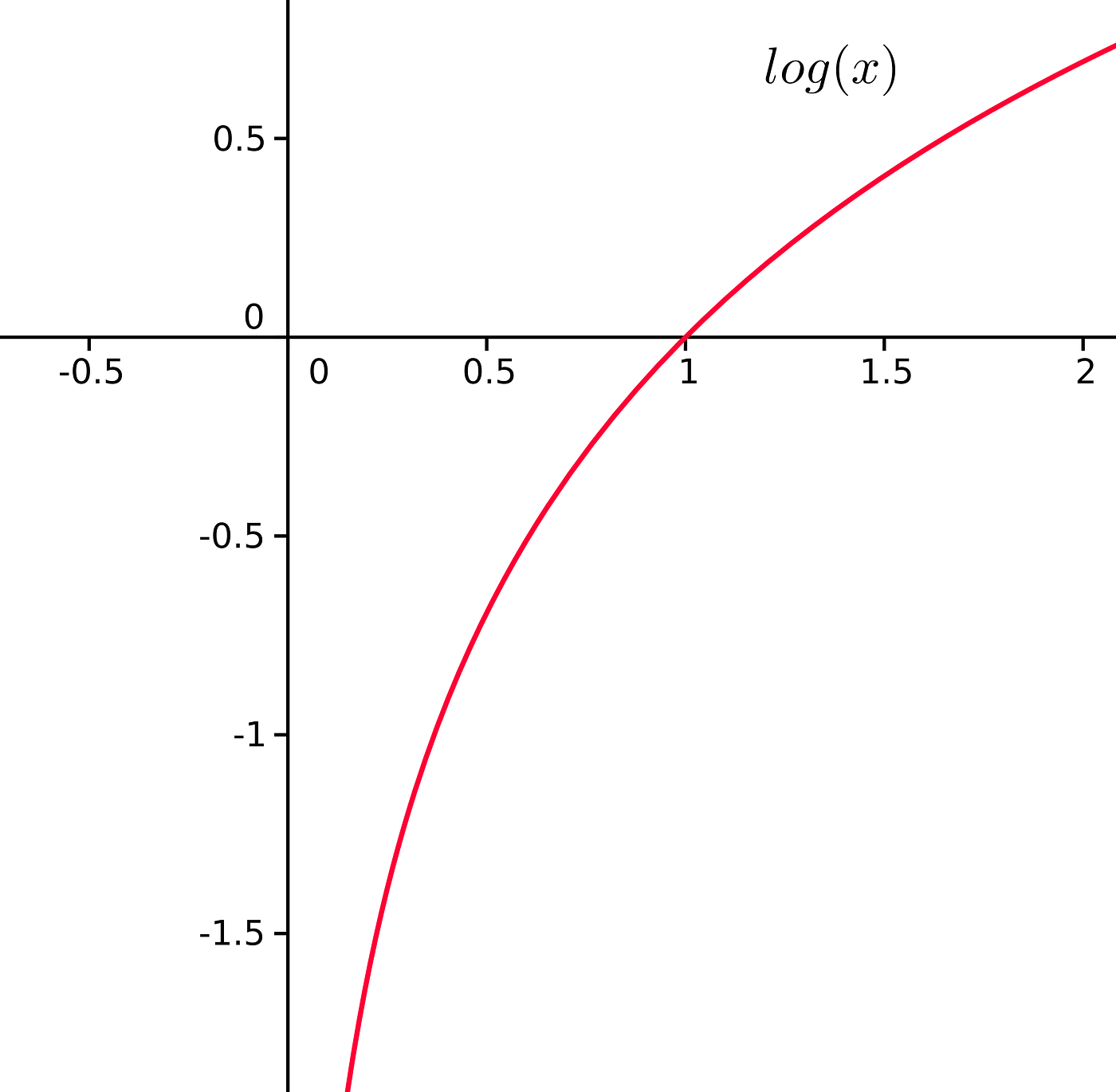
예시를 통해 이게 무엇을 의미하는지 알아보자. 동그라미와 세모를 담은 3개의 컨테이너가 있다고 가정해보자.

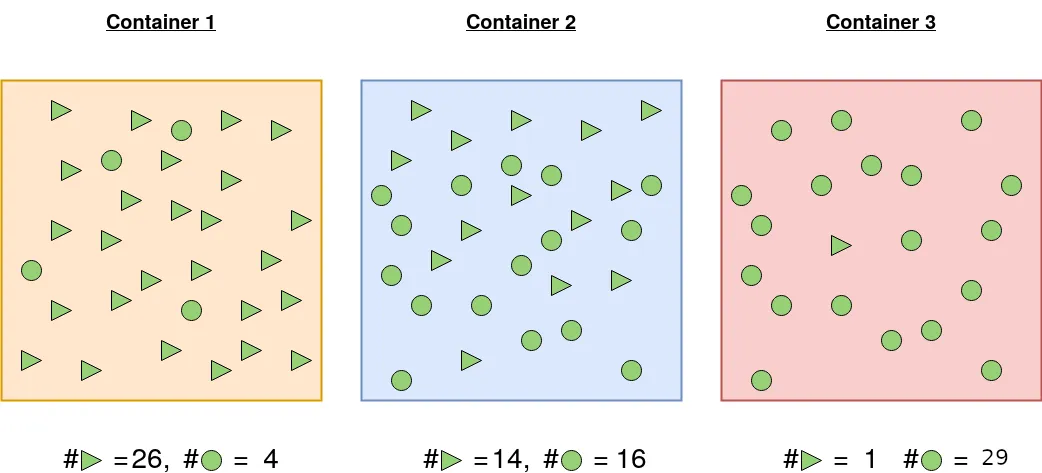
컨테이너 1에서 세모를 뽑을 확률은 $26 \over 30$이고, 동그라미를 뽑을 확률은 $4 \over 30$이다. 따라서 세모를 동그라미보다 더 많이 뽑을 것이란 게 확실하다.

컨테이너 2에서 세모를 뽑을 확률은 $14 \over 30$이고, 동그라미를 뽑을 확률은 $16 \over 30$이다. 세모와 동그라미가 거의 같은 갯수이므로 컨테이너 안에서 하나를 뽑았을 때, 어느 모양인지 확신을 가지고 말할 수 없다.

컨테이너 1에서 세모를 뽑을 확률은 $1 \over 30$이고, 동그라미를 뽑을 확률은 $29 \over 30$이다. 따라서 동그라미를 세모보다 더 많이 뽑을 것이란 게 확실하다.

엔트로피 공식대로 각 컨테이너의 엔트로피를 구해보자. 세모와 동그라미가 균등하게 들어있는 컨테이너 2의 엔트로피가 가장 높은 것을 확인 할 수 있다. 즉, 엔트로피의 값이 높을 수록 불확실한 정도가 높다라고 해석할 수 있다.

2. Cross-Entropy

크로스 엔트로피는 두 확률의 분포가 얼마나 다른지 측정하는 방법이다. 머신러닝과 딥러닝에서는 주로 손실 함수(loss function)로 사용되어 모델의 예측이 실제 레이블과 얼마나 잘 일치하는지 평가하기 위해 사용된다.

$H(p, q) = - \sum p_{i} \log(q_{i})$

크로스 엔트로피는 손실 함수로서의 사용될 때 이진 분류(Binary Classification) 문제나 다중 클래스 분류(Multi-class Classification) 문제에 적용할 수 있다. 이때, 실제 분포 $p(x)$는 원-핫 인코딩(One-Hot Encoding) 형태로 주어지며, 특정 클래스에 대해서만 1의 값을 가지고 나머지는 0의 값을 갖는다.

따라서 크로스 엔트로피를 최소화하는 것은 원-핫 인코딩 레이블에 대한 예측 확률을 최대화하는 것과 같다고 할 수 있다. 따라서 모델은 각 샘플의 실제 클래스에 대해 가능한 한 높은 확률을 예측하려고 하며, 그 결과로 크로스 엔트로피 손실이 낮아진다.

예시를 통해 알아보자. 총 4개의 클래스에 대한 모델의 예측 확률값이 있고, 정답이 원-핫 인코딩 형태로 주어졌다. 모델이 정답 레이블에 대한 예측 확률은 0.775이다.

이때 크로스 엔트로피를 구하면 0.3677이 나온다.

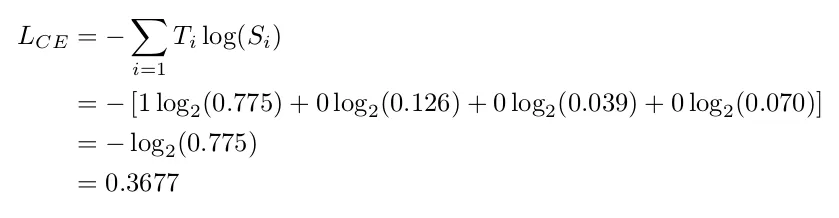
가중치 개선을 통해 모델이 개선되어 모델이 더 정확한 예측을 할 수 있다고 하자. 이때 모델이 정답 레이블에 대해 예측 확률이 0.938로 개선되었다.

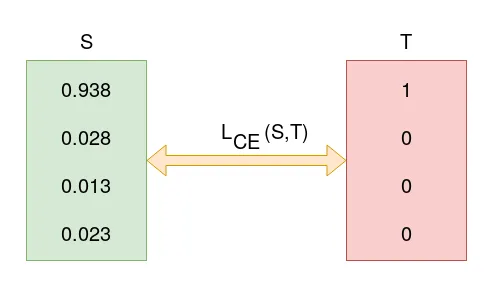
이때 크로스 엔트로피는 0.095으로 이전보다 낮아졌다.

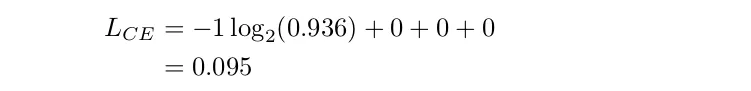
위의 예시를 통해 정답에 대해 더욱 높은 확률로 예측할 수록 크로스 엔트로피 값이 낮아지는 것을 확인할 수 있다. 따라서 크로스 엔트로피를 손실함수로 사용했을 때, 크로스 엔트로피가 낮아질 수록 모델의 예측 정확도가 개선되고 있다고 이해할 수 있다.