03.26 학습&숙제

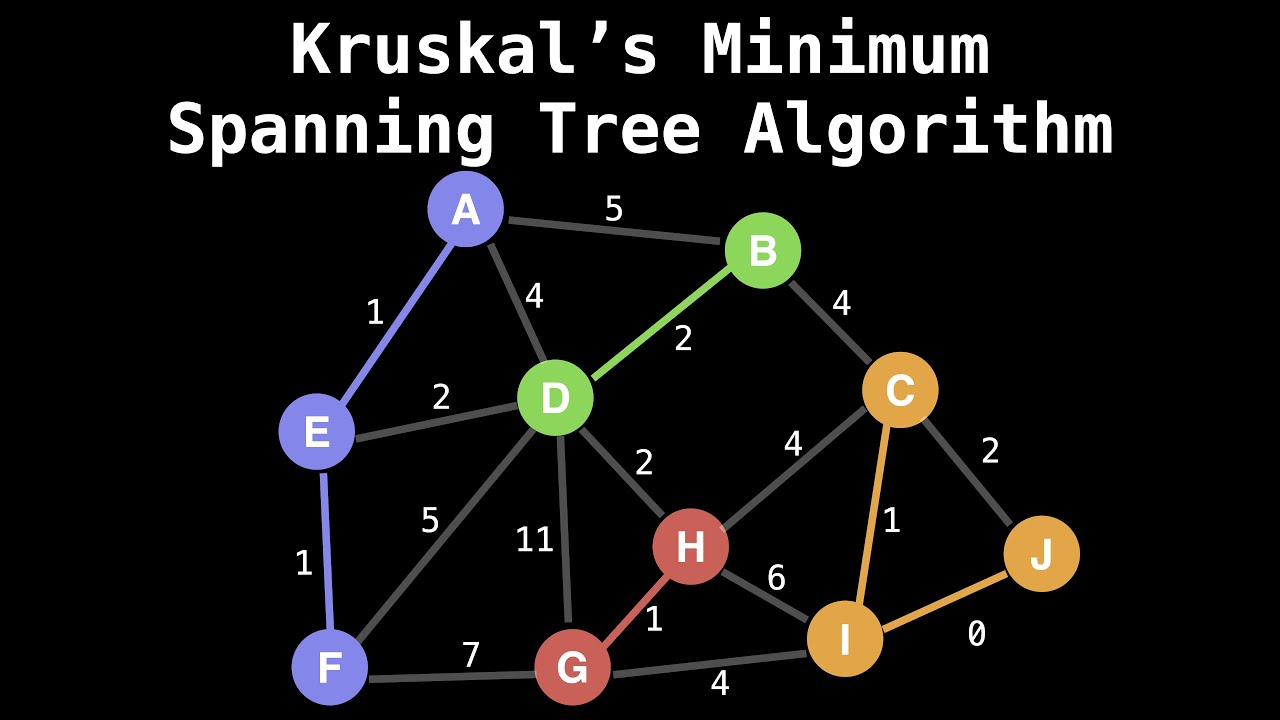
Disjoint Sets Algorithm 🟥🟧🟨🟩🟦🟪🟫⬜⬛🫢🔔😎😊🤔😭⭐

썸네일 출처

서로소 집합

서로소 : 두 수 간에 1을 제외한 공약수가 없다

=> 상호베타집합, 분리집합

확장하면 MST -> 크루스칼, 프림

😎 집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분한다! (대표자)

🔔 표현방법 : 연결 리스트 OR 트리

Make-Set(x) , Find_Set(x), Union(x,y)

⭐ 두 집합이 서로소 상태일때 합집합 연산을 진행한다!

⭐ 원소를 합치는 것이 아닌 집합을 합치는 것을 명심! ⭐

최적화

트리 선택, rank 관리, 경로 압축

🤔 rank를 관리하는데 뭔가 진입차수 같네

경로 압축
return p x = find-set(p x)
로 바로 압축하여 시간 효율 챙긴다!

백준 25545번

정답코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

// 간선의 가중치 합이 최소 신장 트리와도, 최대 신장 트리와도 다른 신장 트리 
// 모든 간선의 가중치가 다른 양방향 연결 그래프
// 모든 간선의 가중치가 다르다
// 최대 MTS와 최소 MST를 제외한 간선 두개를 연결 후 TREE를 만들어주면 답
public class Main_25545 {
    static class Edge{
        int s;
        int e;
        int w;
        int idx;
        public Edge(int s, int e, int w,int idx) {
            super();
            this.s = s;
            this.e = e;
            this.w = w;
            this.idx = idx;
        }
        
    }
    static int N; // 200000
    static int M; // 500000
    static int[] p,r,visitedD,visitedA,resArr;
    static Edge[] edges;
    static PriorityQueue<Edge> pqD,pqA; //최대 최소 크루스칼
    static int cnt,idx;
    public static void main(String[] args) throws NumberFormatException, IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        p = new int[N+1];
        r = new int[N+1];
        resArr = new int[N];
        edges = new Edge[M+1];
        visitedA = new int[M+1];
        visitedD = new int[M+1];
        pqA = new PriorityQueue<>((o1,o2) -> (o1.w - o2.w));
        pqD = new PriorityQueue<>((o1,o2) -> (o2.w - o1.w));
        // 입력 
        for(int i=1;i<M+1;i++) {
            st = new StringTokenizer(br.readLine());
            int s = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            edges[i] = new Edge(s,e,w,i);
            pqA.add(new Edge(s ,e ,w,i));
            pqD.add(new Edge(s, e, w,i));
        }
        
        // MST전 초기화
        for(int i=1;i<N+1;i++) {
            p[i] = i;
            r[i] = 1;
        }
        // 최소 MST
        while(!pqA.isEmpty()) {
            Edge cur = pqA.poll();
            if(union(cur.s,cur.e)) {
                visitedA[cur.idx] = 1;
            }
        }
        
        // MST전 초기화
        for(int i=1;i<N+1;i++) {
            p[i] = i;
            r[i] = 1;
        }
        // 최대 MST
        while(!pqD.isEmpty()) {
            Edge cur = pqD.poll();
            if(union(cur.s,cur.e)) {
                visitedD[cur.idx] = 1;
            }
        }
        // 최종  MMST 위한 초기화
        for(int i=1;i<N+1;i++) {
            p[i] = i;
            r[i] = 1;
        }
        // 최소 연결 간선 제외하고 하나 연결 
        for(int i=1;i<=M;i++) {
            if(visitedA[i] == 0) {
                if(union(edges[i].s,edges[i].e)) {
                    sb.append(i).append(" ");
                    break;
                }
            }
        }
        // 최대 연결 간선 제외하고 하나 연결  
        for(int i=1;i<=M;i++) {
            if(visitedD[i] == 0) {
                if(union(edges[i].s,edges[i].e)) {
                    sb.append(i).append(" ");
                    break;
                }
            }
        }
        // MMST 연결
        for(int i=1;i<=M;i++) {
            if(union(edges[i].s,edges[i].e)){
                sb.append(i).append(" ");
            }
        }
        
        // 간선의 갯수가 작을 경우만 NO
        if(N > M) {
            System.out.println("NO");
        }
        else {
            System.out.println("YES");
            System.out.println(sb.toString());
        }
        
        
    }
    private static boolean union(int s, int e) {
        int S = find(s);
        int E = find(e);
        if(S==E)return false;
        if(r[S] < r[E]) {
            r[E] += r[S];
            p[S] = E;
        }else {
            r[S] += r[E];
            p[E] = S;
        }
        return true;
    }
    private static int find(int e) {
        if(p[e] == e) return e;
        else return p[e] = find(p[e]);
    }
}

숙제

벨로그 정리하고 다음주 시험 대비!