03.27 학습&숙제

한강섭·2025년 3월 27일

학습 & 숙제

목록 보기

53/103

썸네일 출처

Minimum Spanning Tree 🟥🟧🟨🟩🟦🟪🟫⬜⬛🫢🔔😎😊🤔😭⭐

최소 신장 트리

그래프에서 최소 비용 문제
1. 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
2. 두 정점 사이의 최소 비용의 경로 찾기

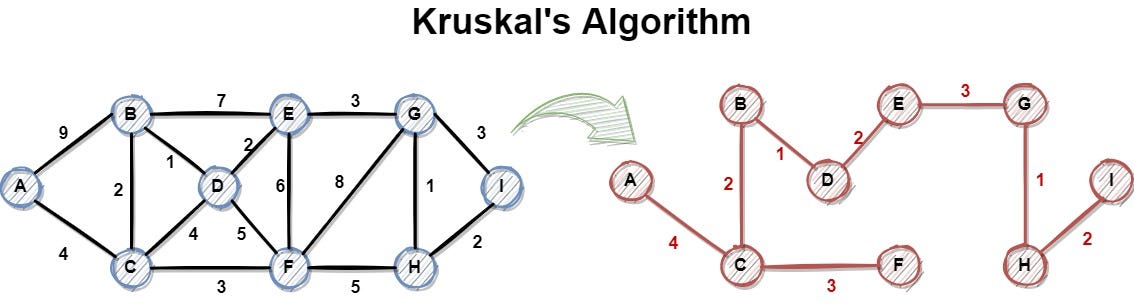
KRUSKAL 알고리즘

간선을 하나씩 선택해서 MST를 찾는 알고리즘
1. 최초, 모든 간선을 가중치에 따라 오름차순 정렬
2. 가중치가 가장 낮은 간선부터 선택하면서 트리 증가시킴
3. n-1개의 간선이 선택될 때까지 2를 반복

PRIM 알고리즘

하나의 정점에서 연결된 간선들 중에 하나씩 선택하면서 MST를 만들어 가는 방식
1. 임의 정점을 하나 선택해서 시작
2. 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
3. 모든 정점이 선택될 때 까지 2과정 반복

서로소인 2개의 집합 정보를 유지
트리 정점 VS 비트리 정점

연습 문제

정답 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int n,m,k;
    static int[] p,r,know;
    static int[][] mem;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        p = new int[n+1];
        r = new int[n+1];
        for(int i=1;i<=n;i++){
            p[i] = i;
            r[i] = 1;
        }
        know = new int[n+1];
        mem = new int[51][51];

        st = new StringTokenizer(br.readLine());
        k = Integer.parseInt(st.nextToken());
        for(int i=0;i<k;i++){
            know[Integer.parseInt(st.nextToken())] = 1;
        }
        for(int i=0;i<m;i++){
            st = new StringTokenizer(br.readLine());
            k = Integer.parseInt(st.nextToken());
            mem[i][0] = k;
            int cur = Integer.parseInt(st.nextToken());
            mem[i][1] = cur;
            for(int j=1;j<k;j++){
                int next = Integer.parseInt(st.nextToken());
                mem[i][j+1] = next;
                union(cur,next);
                cur = next;
            }
        }

        int cnt=0;
        for(int i=0;i<m;i++){
            k = mem[i][0];
            int flag = 0;
            for(int j=1;j<=k;j++){
                if(know[find(mem[i][j])] == 1){
                    flag =1;
                    break;
                }
            }
            if(flag == 0) {
                cnt++;
            }
        }
        System.out.println(cnt);
    }

    private static void union(int cur, int next) {
        int C = find(cur);
        int N = find(next);
        if(C==N) return;
        if(know[C] == 1){
            p[N]=C;
        }
        else{
            p[C]=N;
        }
    }
    private static int find(int next) {
        if (p[next] == next) return next;
        else {
            return p[next] = find(p[next]);
        }
    }
}