04.09 학습&숙제

---

모든 쌍 최단 경로

한 도시에서 다른 도시로 가장 빨리 갈 수 있는 경로를 찾는 문제

가중치 포함, 방향성 그래프에서 최단경로 찾기

각 정점을 시작 정점으로 다익스트라를 수행한다

인접행렬을 사용하면 O(n^3) n 정점의 수

하지만 플로이드를 써도 O(n^3) 시간은 같고 구현은 훨씬 쉽다

---

DP 접근

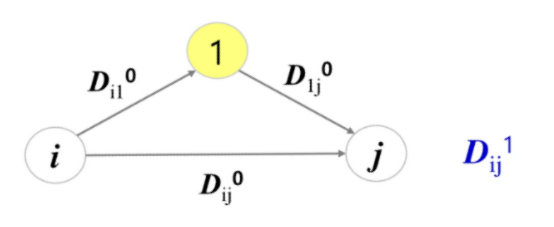
정점 1로부터 시작하여, 정점 1과 2, 그 다음엔 정점 1,2,3으로 하나씩 추가하여, 마지막에는 정점 1~n까지의 모든 정점을 경유 가능한 정점들로 고려하면서, 모든 쌍의 최단 경로의 거리를 계산한다.

---

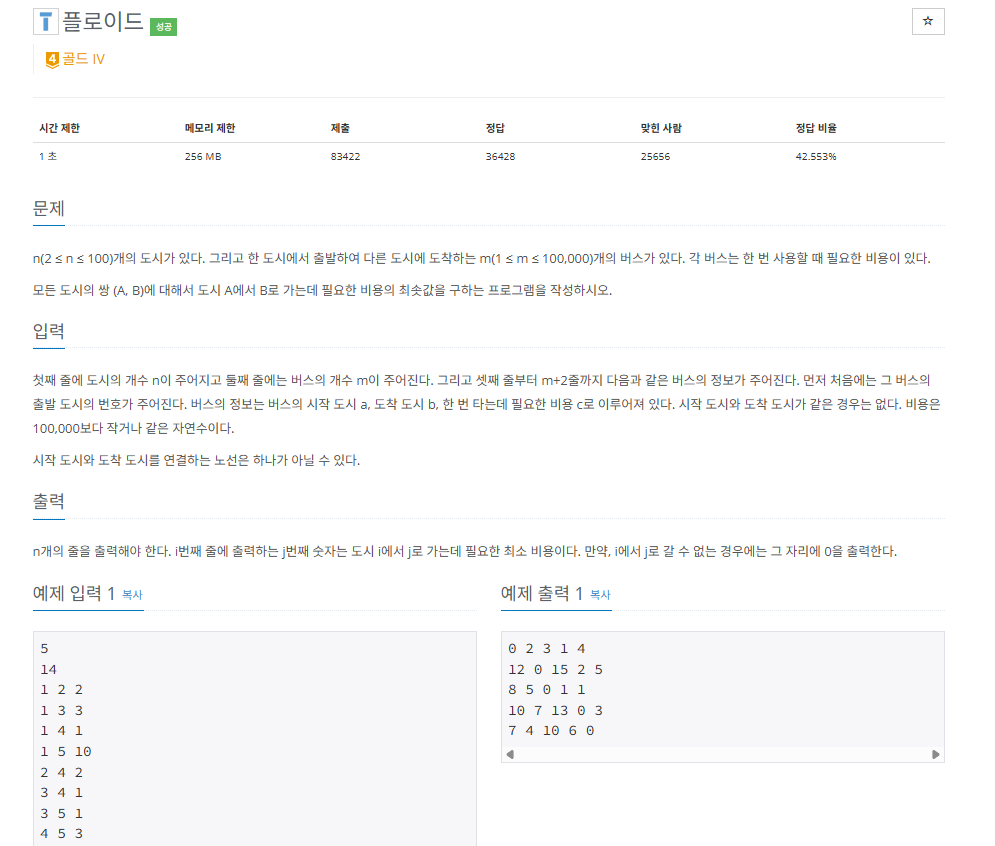
백준 11404: 플로이드

---

정답 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.sql.Array;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.StringTokenizer;

public class Main {
    static int n;
    static int m;
    static long[][] dist;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        n = Integer.parseInt(br.readLine());
        m = Integer.parseInt(br.readLine());
        dist = new long[n+1][n+1];

        for(int i=0;i<n+1;i++){
            for(int j=0;j<n+1;j++){
                if(i==j)dist[i][j] = 0;
                else dist[i][j] = Integer.MAX_VALUE;
            }
        }

        for(int i=0;i<m;i++){
            st = new StringTokenizer(br.readLine());
            int s = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            dist[s][e] = Long.min(dist[s][e], w);
        }

        for(int k=1;k<=n;k++){
            for(int i=1;i<=n;i++){
                for(int j=1;j<=n;j++){
                    dist[i][j] = Long.min(dist[i][j], dist[i][k]+dist[k][j]);
                }
            }
        }

        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(dist[i][j]==Integer.MAX_VALUE){
                    sb.append("0 ");
                }
                else{
                    sb.append(dist[i][j]+" ");
                }
            }
            sb.append("\n");
        }

        System.out.println(sb.toString());


    }
}

---

숙제

벨로그 정리 + 정처기 실기 정리!

---