04.08 학습&숙제

한강섭·2025년 4월 8일

LIS 숙제 학습

학습 & 숙제

목록 보기

60/103

최장 증가 부분 수열

3,2,6,4,5,1
다음과 같은 수열의 순서를 유지하면서 크기가 점진적으로 커지는 가장 긴 부분 수열의 길이는 얼마일까?

2,4,5 or 3,4,5 답은 3!

완전 탐색을 하면

O(2^n) 시간 필요;;

DP

dp 접근을 한다면

LIS(i)를 LIS(1), LIS(2), LIS(I-1) 와의 관계로 표현 할 수 있을까?

안된다..

증가 수열의 관계인 aj를 찾고 j값을 알 수 없으니 모두 검색해야 한다

O(n^2)으로 시간 단축!

이진 검색 활용

각 길이를 LIS로 만족하는 가장 끝에 오는 최소값을 구해주면 길이를 알 수 있다!

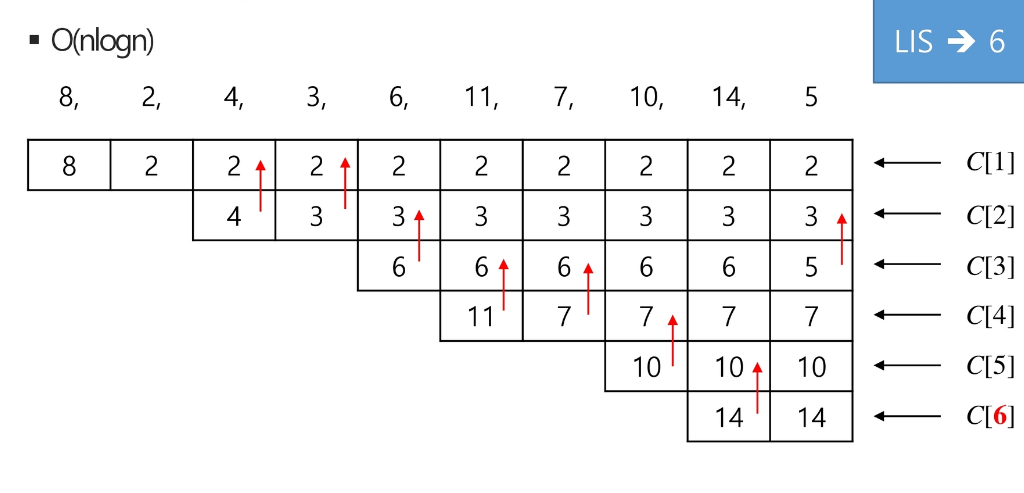
이분 탐색을 활용해서 O(nlogn)으로 시간 더 단축!

백준 11054번 가장 긴 바이토닉 부분 수열

정답 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	static int n, res;
	static int[] arr;
	static int[][] dp;
	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		n = Integer.parseInt(br.readLine());
		arr = new int[n+1];
		dp = new int[n+1][2];
		
		st = new StringTokenizer(br.readLine());
		
		for(int i=1;i<n+1;i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		
		res = -1;
		for(int i=1;i<n+1;i++) {
			int max0 = -1;
			int max1 = -1;
			for(int j=0;j<=i-1;j++) {
				// arr[i]가 더 클때는 dp[0] 에서 더한 값 
				if(arr[i] > arr[j]) {
					max0 = dp[j][0] > max0 ? dp[j][0] : max0; 
				}
				// arr[i]가 더 작을 때는 dp[0] 에서 더한 값을 dp[1]에 저장
				// + dp[1] 에서 그냥 더한 값
				else if(arr[i] < arr[j]){
					max1 = dp[j][0] > max1 ? dp[j][0] : max1;
					max1 = dp[j][1] > max1 ? dp[j][1] : max1;
				}
				
				dp[i][0] = max0 + 1;
				dp[i][1] = max1 + 1;
				
				res = res < dp[i][0] ? dp[i][0] : res;
				res = res < dp[i][1] ? dp[i][1] : res;
				
			}
		}
		
//		for(int i=0;i<n+1;i++) {
//			System.out.println(dp[i][0] + " " + dp[i][1]);
//		}
			
		System.out.println(res);
	}
}