시작하기 전에

• 이번에 다룰 내용은 다음 두 조건을 만족하는 상황입니다.

  1. 작은 문제 (상태 집합 S 나 액션 집합 A 의 크기가 작은 경우)
  2. MDP 를 알 때

• 이번에 다룰 문제는 작은 문제이기 때문에, 테이블 기반 방법론 에 기반합니다.

  • 테이블 기반 방법론이란 모든 상태 s 혹은 상태와 액션의 페어 (s, a) 에 대한 테이블을 만들어서 값을 기록해 놓고, 그 값을 조금씩 업데이트하는 방식을 의미합니다.

밸류 평가하기 - 반복적 정책 평가

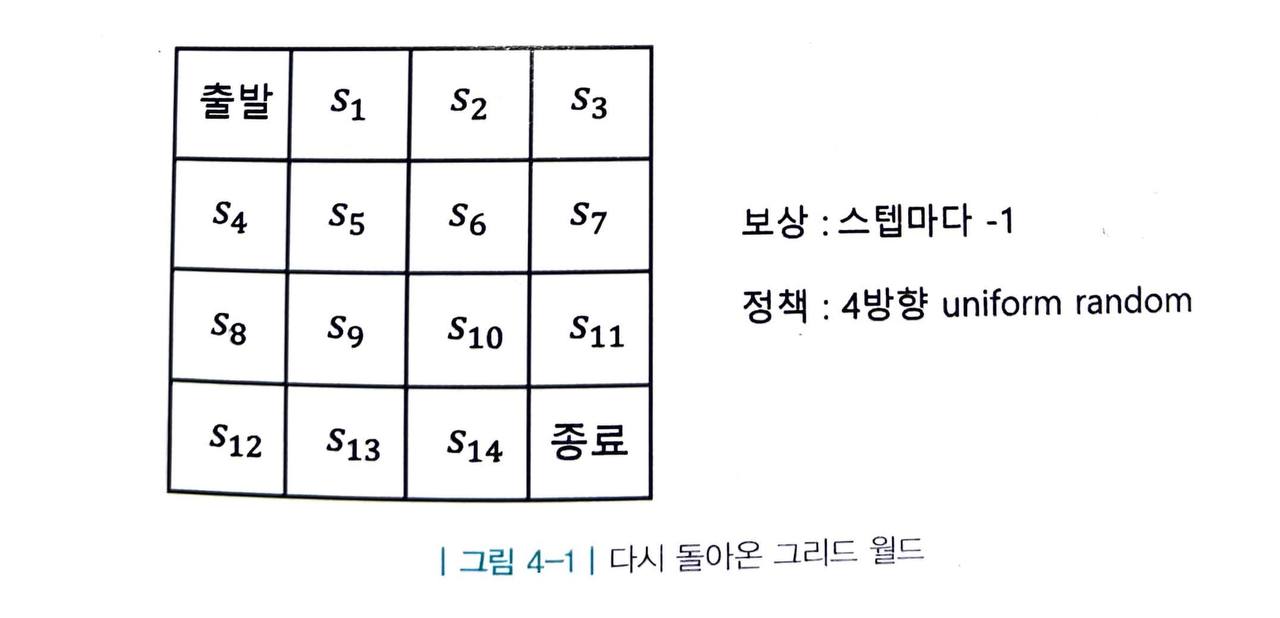
• 이 문제는 4방향 랜덤이라는 정책 함수 π 가 주어졌고 이 때 각 상태 s 에 대한 가치 함수 v(s) 를 구하는 전형적인 prediction 문제입니다.

• 이제 반복적 정책 평가 라는 방법론을 통해 문제를 해결할 수 있습니다.

  • 반복적 정책 평가는 테이블의 값들을 초기화한 후, 벨만 기대 방정식을 반복적으로 사용하여 테이블에 적어 놓은 값을 조금씩 업데이트해 나가는 방법론입니다.

• 또한 이 방법론은 MDP 에 대한 모든 정보를 알 때 사용할 수 있습니다.

  • 보상은 어느 액션을 하든 -1이므로 r(s, a) = -1 로 모든 액션에 대해 고정입니다.
  • 또한 환경에 확률적인 요소가 없기 때문에 전이 확률 P(s, a, s') 은 모두 1입니다.

• 본 문제에서 편의상 γ=1 로 계산하여 반복적 정책 평가 방법론을 단계별로 나누어 자세히 설명하겠습니다.

1. 테이블 초기화

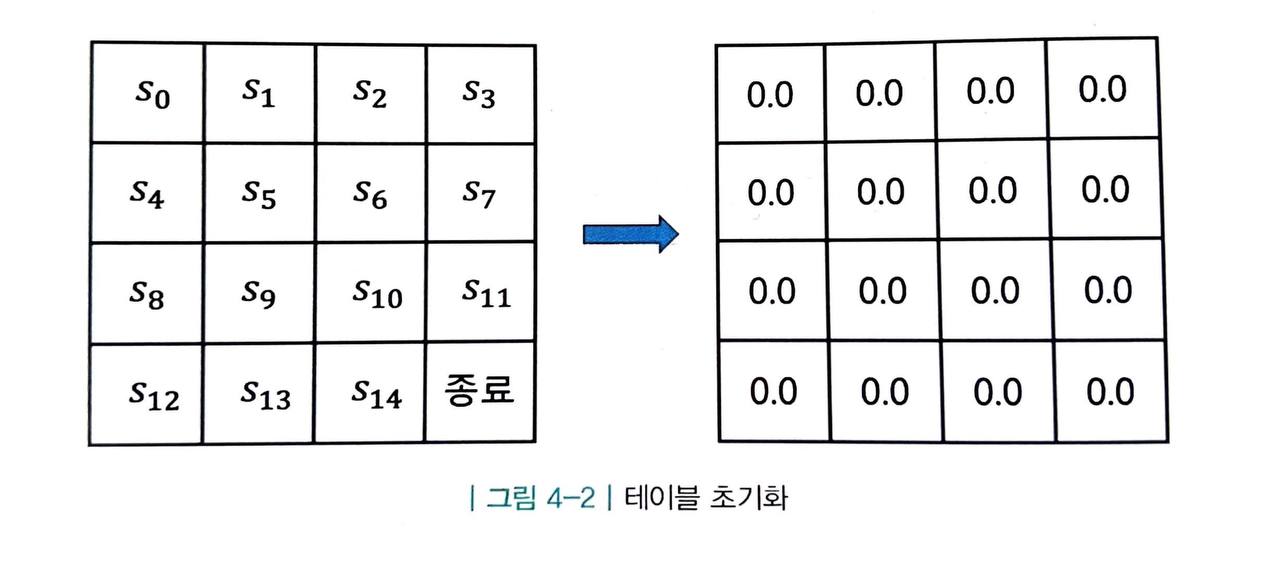
• 먼저 테이블을 초기화하는 것으로부터 시작합니다.

  • 어떤 값으로 초기화해도 상관없지만, 일단 0으로 초기화합시다.

• 지금은 아무 의미가 없는 값이지만 반복적 과정을 거치면서 점차 실제 각 상태의 가치에 해당하는 값으로 수렴해 갈 것입니다.

2. 한 상태의 값을 업데이트

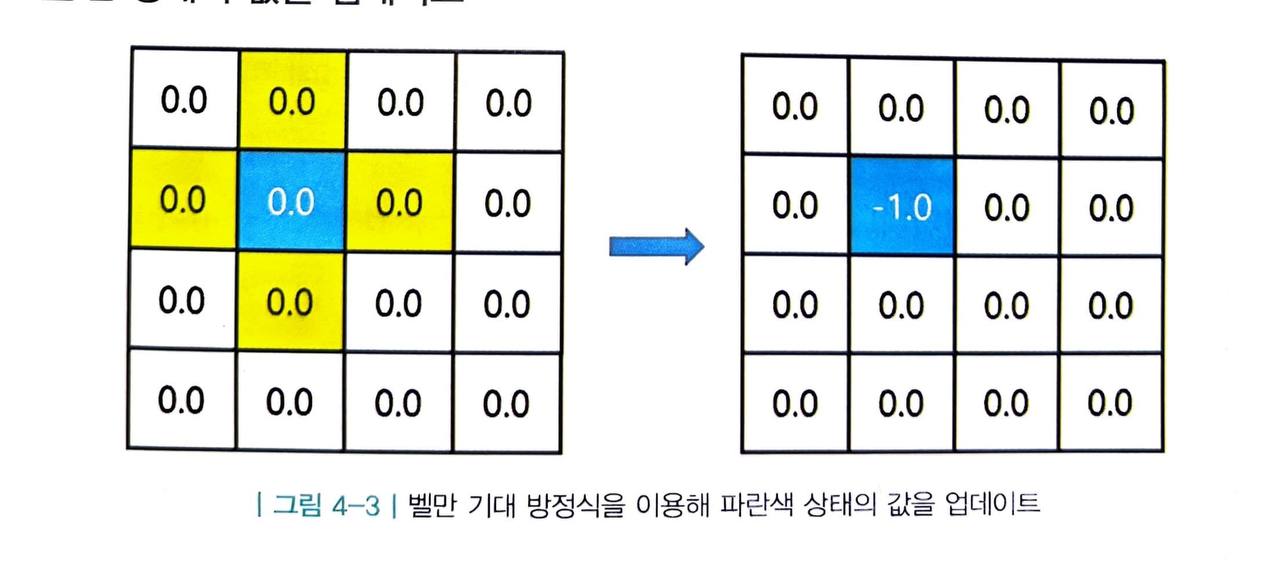
• 일단 16개의 값들 중 1개의 값에 대해 어떻게 업데이트하는지 설명하겠습니다.

  • 위 그림에서 파란색으로 칠해진 상태 s5 를 생각해 봅시다.

• 우리는 MDP 를 알기 때문에 이 상태의 다음 상태의 후보가 동서남북으로 인접해 있는 노란색 상태들인 것을 알 수 있습니다.

  • 현재 상태와 다음 상태의 밸류 사이 관계식인 벨만 기대 방정식의 2단계 수식을 사용합시다.

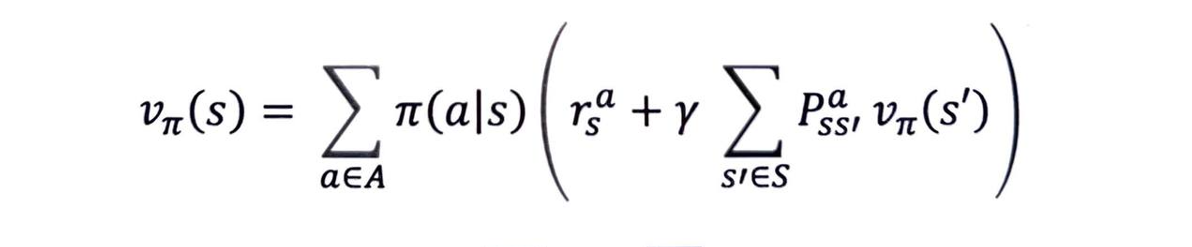
• 여기서 정책 함수는 4방향으로 균등하게 랜덤하므로 π(aㅣs) 는 모든 액션에 대해 각각 0.25입니다.

• 이를 토대로 실제 값을 대입하여 다음과 같이 간단하게 계산할 수 있습니다.

• 따라서 테이블의 s5 자리 값을 -1.0으로 업데이트합니다.

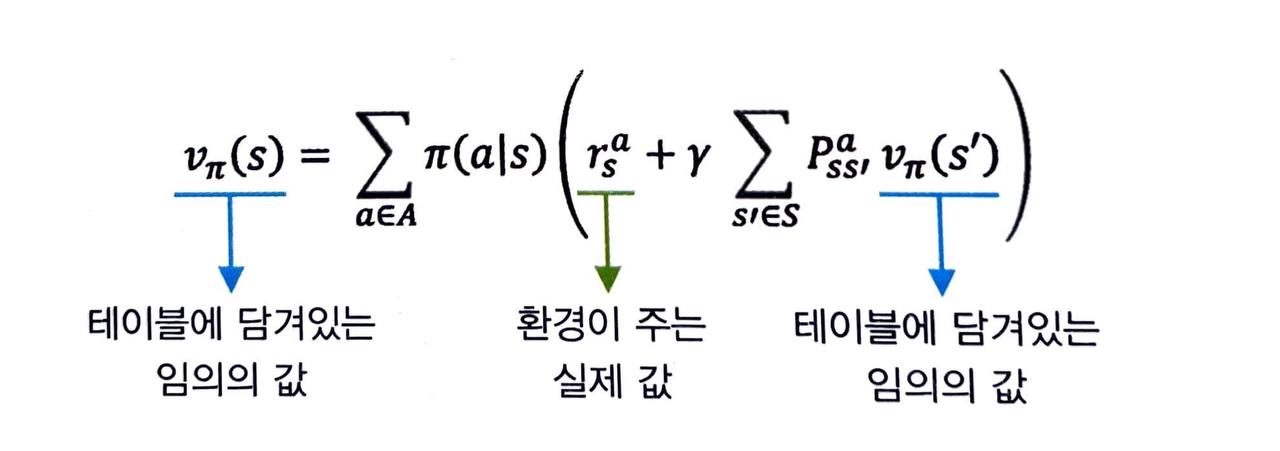
• 임의로 정해진 0이라는 값을 이용해 현재 상태의 값을 업데이트하는 게 왜 더 정확한 값이 디는 것일까요?

• 우리는 다음 상태의 값만 가지고 업데이트 하는 것이 아니라, 보상이라는 실제 환경이 주는 정확한 시그널을 섞어서 업데이트합니다.

  • 따라서 처음에는 무의미 하더라도 점차 실제 값에 가까워지게 됩니다.

• 게다가 다음 상태의 값이 항상 엉터리인 것은 아닙니다.

  • 오른쪽 맨 아래 상태인 "종료 상태"의 경우 가치가 0으로 초기화 되어있는데, 종료 상태의 입장에서는 그 뒤의 미래라는 것이 존재하지 않기 때문에 정확한 값입니다.

• 따라서 마지막 상태에 인접한 상태들의 경우, 더 유의미한 시그널을 통해 업데이트가 이루어집니다.

3. 모든 상태에 대해 2의 과정을 적용

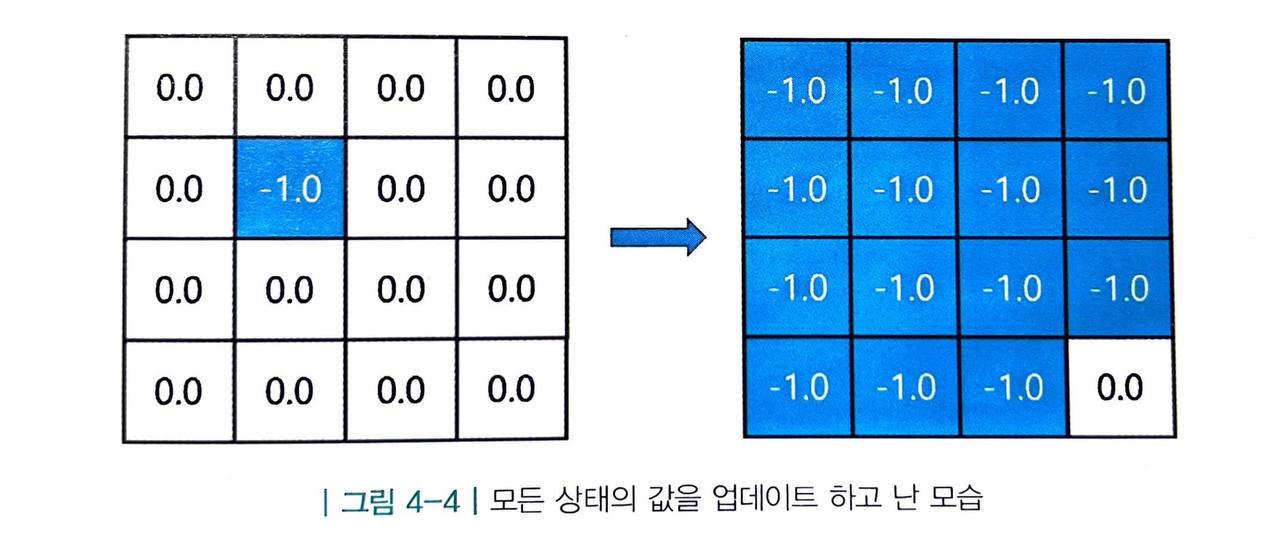
• 마지막 상태를 제외한 15개의 상태를 업데이트합니다.

  • 참고로 가장자리에서 바깥을 향하는 액션을 취하면 같은 자리에 그대로 남게 됩니다.

• 모든 상태의 값을 업데이트하고 나면 비로소 한 바퀴를 돈 것입니다.

  • 종료 상태를 제외한 모든 상태의 값이 -1로 업데이트되었습니다.

4. 앞의 2~3 과정을 계속해서 반복

• 이렇게 한 번 테이블의 모든 값을 업데이트하는 과정을 여러 번 반복합니다.

  • 몇 번 반복했는지를 k로 표기하겠습니다.

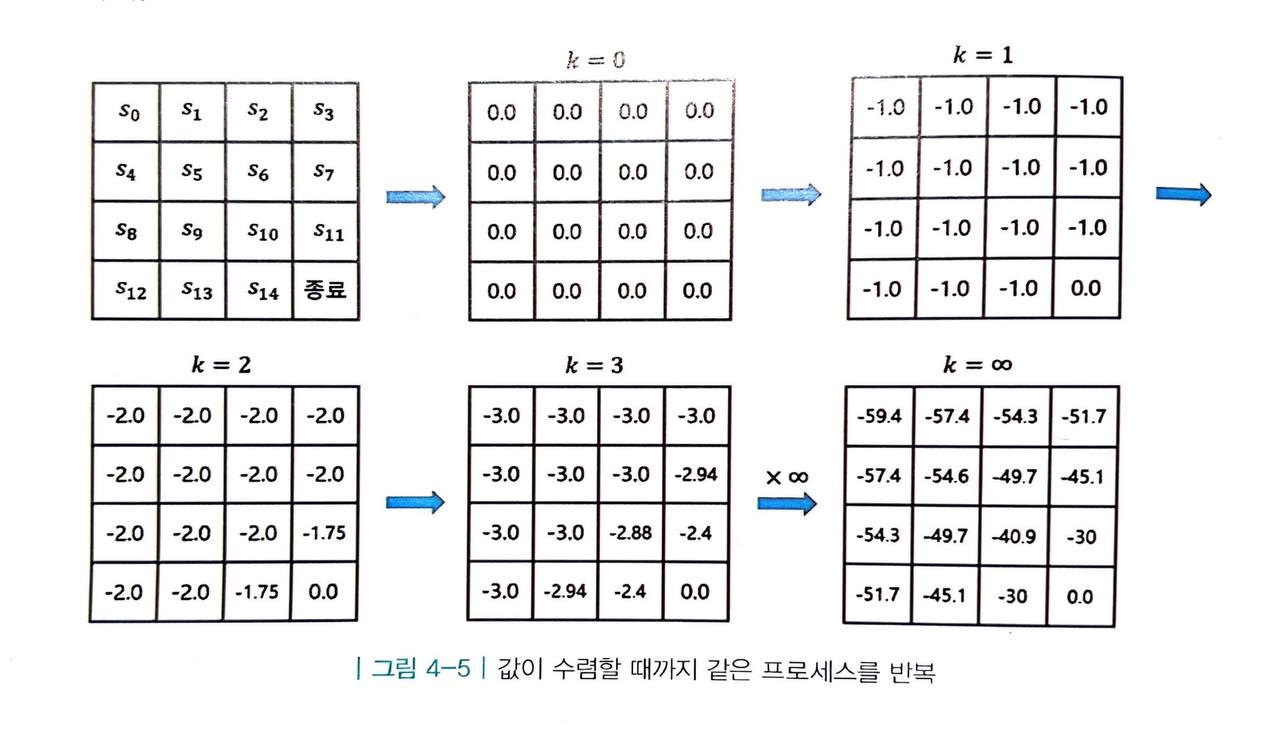
• 이 과정을 계속하다 보면 각 상태의 값이 어떤 값에 수렴하게 됩니다.

  • 그 값이 바로 해당 상태의 실제 밸류입니다.

정리

• 지금까지 우리는 정책 π 가 주어졌을 때 각 상태의 밸류를 계산하는 법을 배웠습니다.

• MDP 에 대한 정보를 알고 그 크기가 충분히 작다면, 그 어떤 정책 함수에 대해서도 해당 정책 함수를 따랐을 때 각 상태의 밸류를 구할 수 있게 됩니다.

최고의 정책 찾기 - 정책 이터레이션

• 정책 이터레이션은 정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때까지 반복하는 방법론입니다.

• 앞서 배운 반복적 정책 평가의 결과를 잠시 생각해 봅시다.

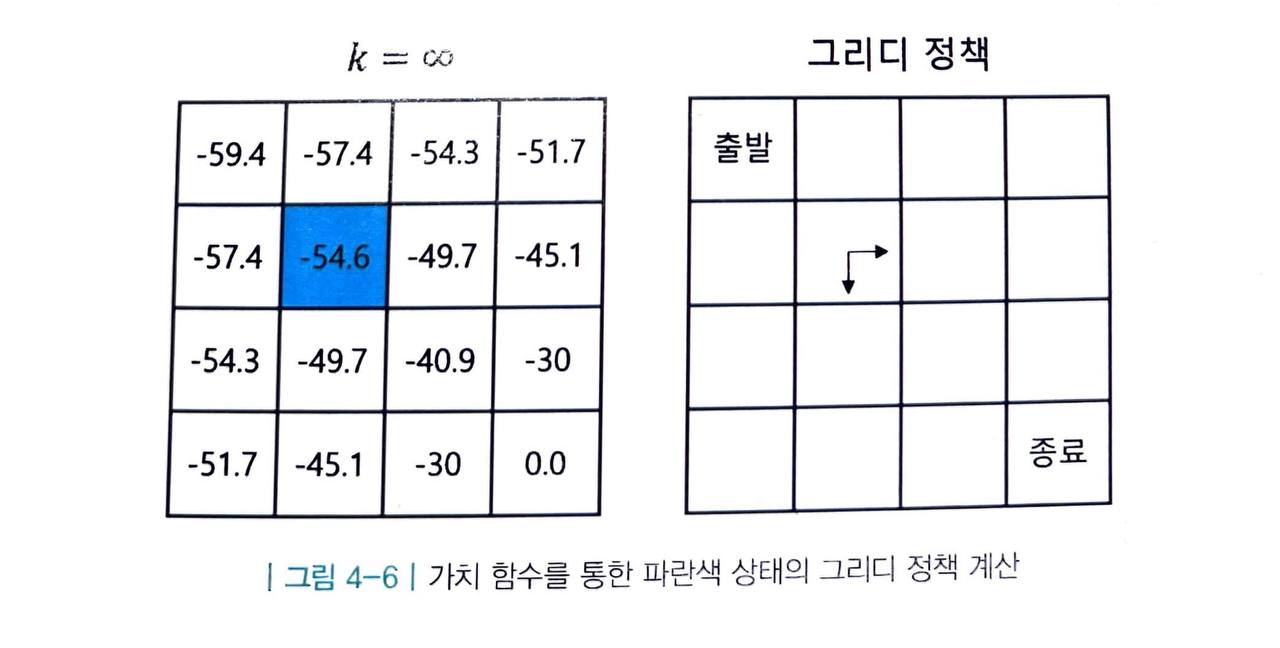
• 여기서 우리가 파란색 상태인 s5 에 있다고 생각해 봅시다.

  • s5 에서는 동쪽 혹은 남쪽으로 움직이는 a 를 선택하는 것이 최선입니다.

• 따라서 다음과 같은 정책 π' 을 생각해볼 수 있습니다.

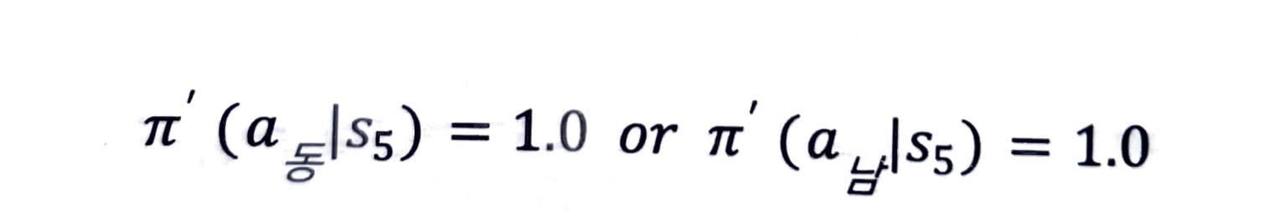
• 이렇게 만들어진 π' 은 원래의 정책 π 보다는 나은 정책입니다.

  • 이러한 정책을 그리디 정책 이라고 합니다.

• 여기서 그리디 는 탐욕스럽다는 뜻으로 먼 미래까지 보지 않고 그저 눈 앞의 이익을 최대화하는 선택을 취하는 방식을 뜻합니다.

• 그러면 재미있는 결과를 얻게 됩니다.

  • 바로 s5 에서의 그리디 정책이 s5 에서의 최적 정책과 일치하는 것이죠.

• 요약하면 이상한 정책(랜덤 정책)의 가치를 평가했을 뿐인데 s5 에서의 더 나은 정책을 알게 된 것입니다. 그렇다면 마찬가지 방법으로 모든 상태에서 더 나은 정책을 알 수 있지 않을까요?

• s5 뿐만 아니라 모든 상태에 대해 그리디 정책을 표기한 결과는 다음 그림과 같습니다.

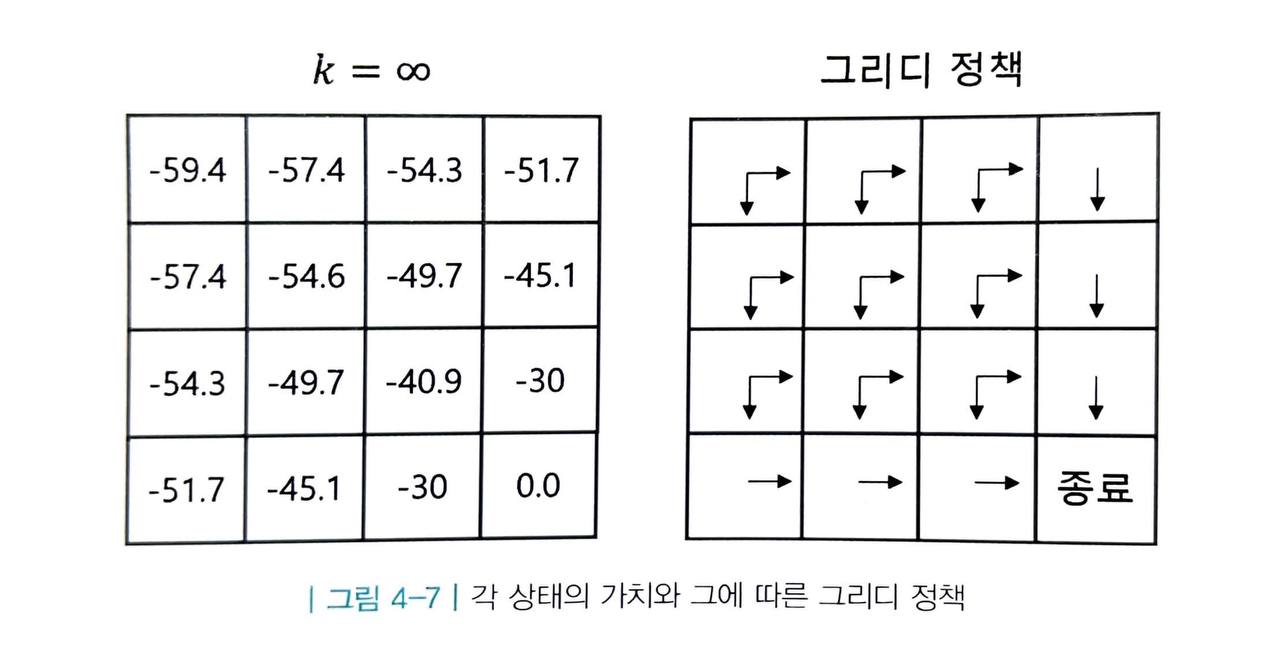
• 놀랍게도 모든 상태에서 그리디 액션을 택했을 뿐인데 더 나은 정책 π' 을 얻었습니다.

• 본 예시에서는 π' 이 최적 정책과 일치하는데 이런 경우는 많지 않습니다.

  • 대개는 이전 정책에 비해 소폭 향상되는 정도입니다.

• 여기서 중요한 부분은 π' 이 π 에 비해 개선되었다는 점입니다.

  • 이것이 바로 이번에 배울 정책 이터레이션 의 핵심입니다.

평가와 개선의 반복

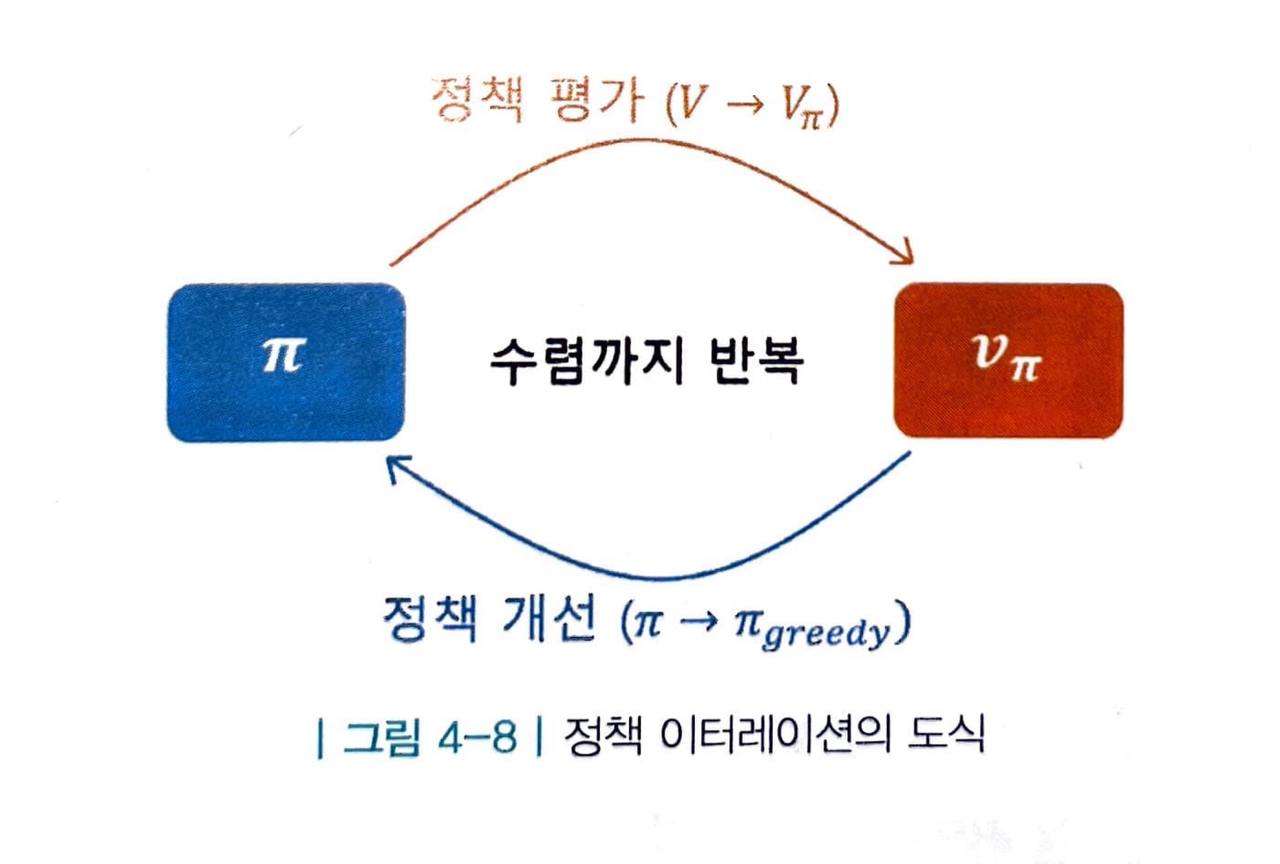
• 정책 이터레이션은 총 2단계로 이루어져 있습니다.

  1. 정책 평가 : 고정된 π 에 대해 "반복적 정책 평가" 방법론을 사용해 각 상태의 밸류를 구합니다.
  2. 정책 개선 : 새로운 정책(그리디 정책) π' 를 생성합니다.

• 그리고 생성된 π' 에 대해 다시 정책 평가를 진행합니다.

  • 즉, 정책의 평가와 개선을 반복하는 것입니다.

• 그러다보면 어느 순간 정책도 변하지 않고, 그에 따른 가치도 변하지 않는 단계에 도달하게 됩니다.

  • 이렇게 수렴하는 곳이 바로 최적 정책 과 최적 가치 가 됩니다.

• 참고로, 그리디 정책 π' 는 기존 정책 π 에 비해 나은 정책으로 이어집니다.

  • 이는 보장된 사실이므로 안심하셔도 좋습니다.

정책 평가 부분을 간소화하기

• 정책 이터레이션은 루프 안에 루프가 있기 때문에 많은 연산을 필요로 합니다. 이 과정을 풀어서 도식화하면 다음 그림과 같습니다.

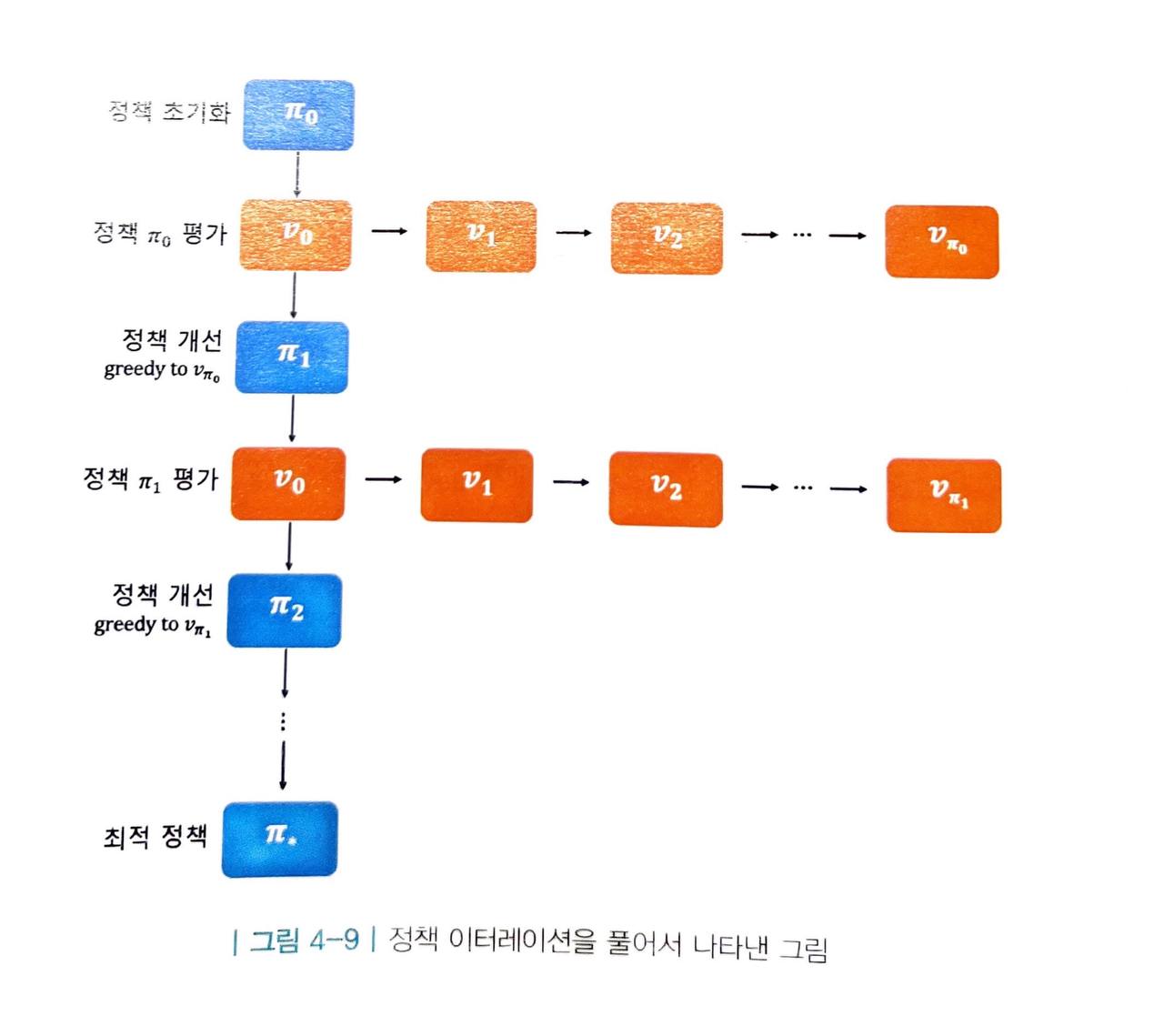
• 위 루프에서 연산을 가장 많이 필요로 하는 단계는 사실 "정책 개선" 단계 보다는 "정책 평가" 단계입니다.

  • 평가 단계에서는 "반복적 정책 평가" 방법을 사용하기 때문에 평가하는 데에도 여러 스텝이 필요합니다.

• 그런데 과연 평가를 끝까지 해야할까요?

  • 우리의 목적은 최고의 정책을 찾는 것이지 정확한 가치를 평가하는 것이 아닙니다.
  • 실제로 정책 이터레이션에서는 가치 함수가 오로지 그리디 정책을 찾는 데에만 쓰일 뿐 테이블에 적혀 있는 구체적 값이 사용되지는 않습니다.

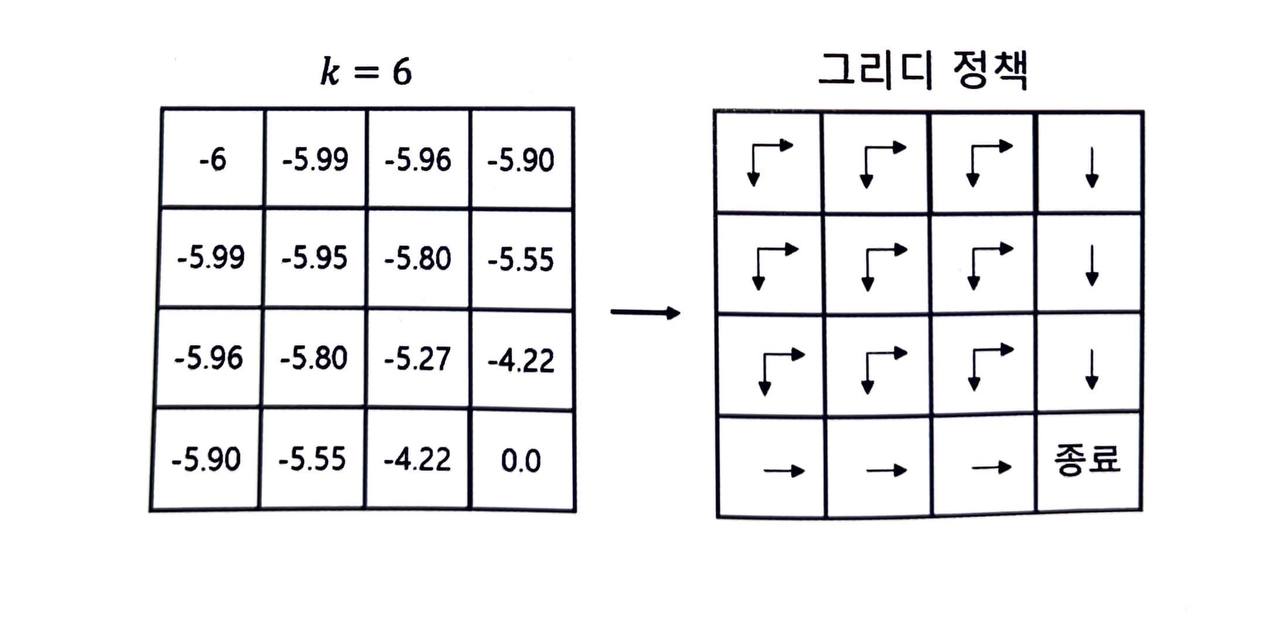
• 위의 예시에서는 6번만 업데이트해도 그리디 정책이 이미 최적 정책에 도달하게 됩니다.

• 심지어 극단적으로는 단 한 번만 업데이트해도 됩니다.

  • 그리디 정책이 현재의 정책과 조금이라도 다르기만 하면 일단은 "개선"할 수 있고, "개선"하여 새로운 정책을 얻은 순간 이전에 구했던 가치 테이블은 버려지게 됩니다.

• 그래서 극단적으로 정책 평가 단계에서 반복적 정책 평가를 딱 k=1 까지만 진행하도록 하겠습니다.

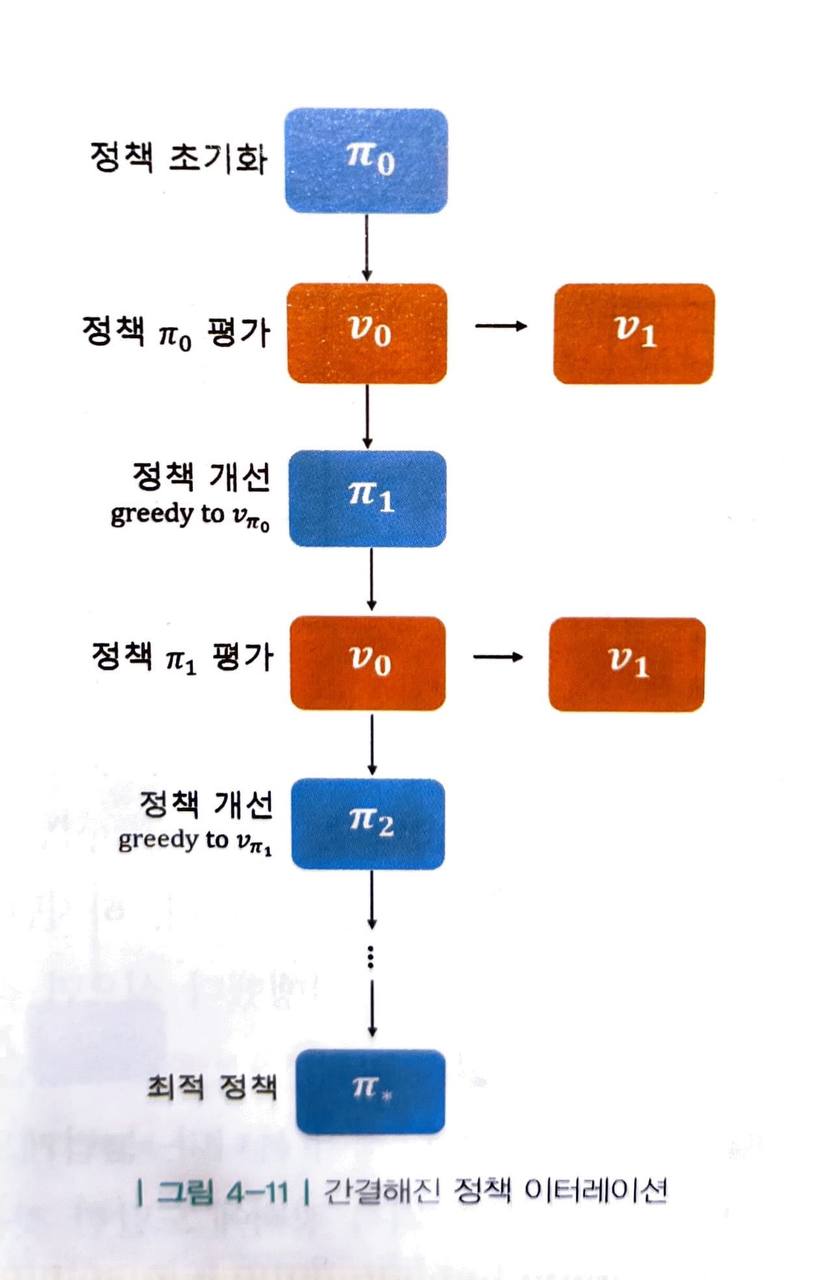
• 한결 간단해졌습니다.

• 요점은 정책 평가 단계에서 가치가 수렴할 때까지 과정을 반복하지 않아도 된다는 것입니다.

  • 간결해진 정책 이터레이션을 통해 우리는 더욱 빠르게 평가와 개선을 진행할 수 있고, 그만큼 빠르게 최적 정책을 찾을 수 있습니다.

최고의 정책 찾기 - 밸류 이터레이션

• 밸류 이터레이션은 오로지 최적 정책이 만들어내는 최적 밸류 하나만 바라보고 달려갑니다.

  • 이는 벨만 최적 방정식을 이용해 단번에 최적의 정책을 찾습니다.

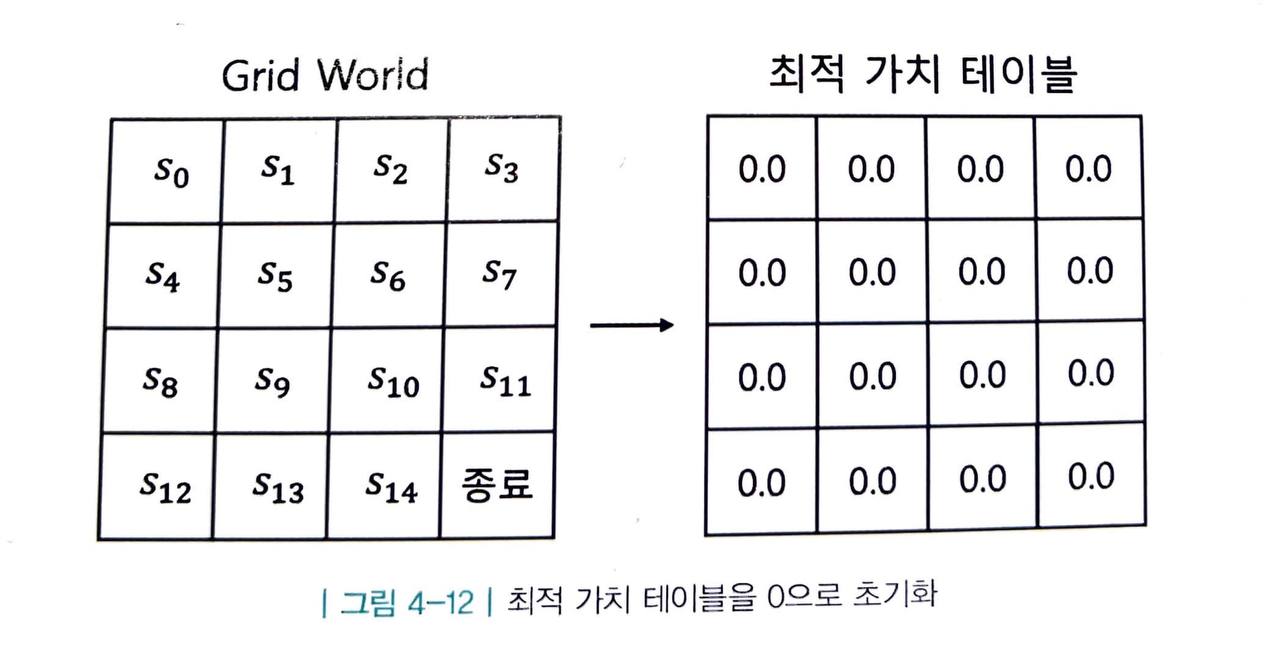
• 우선 테이블을 초기화합니다.

• 정책 이터레이션에서 봤던 그림과 유사하지만 테이블에 담겨 있는 값들은 이번에는 다른 의미를 갖고 있습니다.

  • 정책 이터레이션에서는 해당 평가 단계에서 사용하는 정책 π 의 밸류였지만, 여기서는 최적 정책 π* 의 밸류를 뜻합니다.

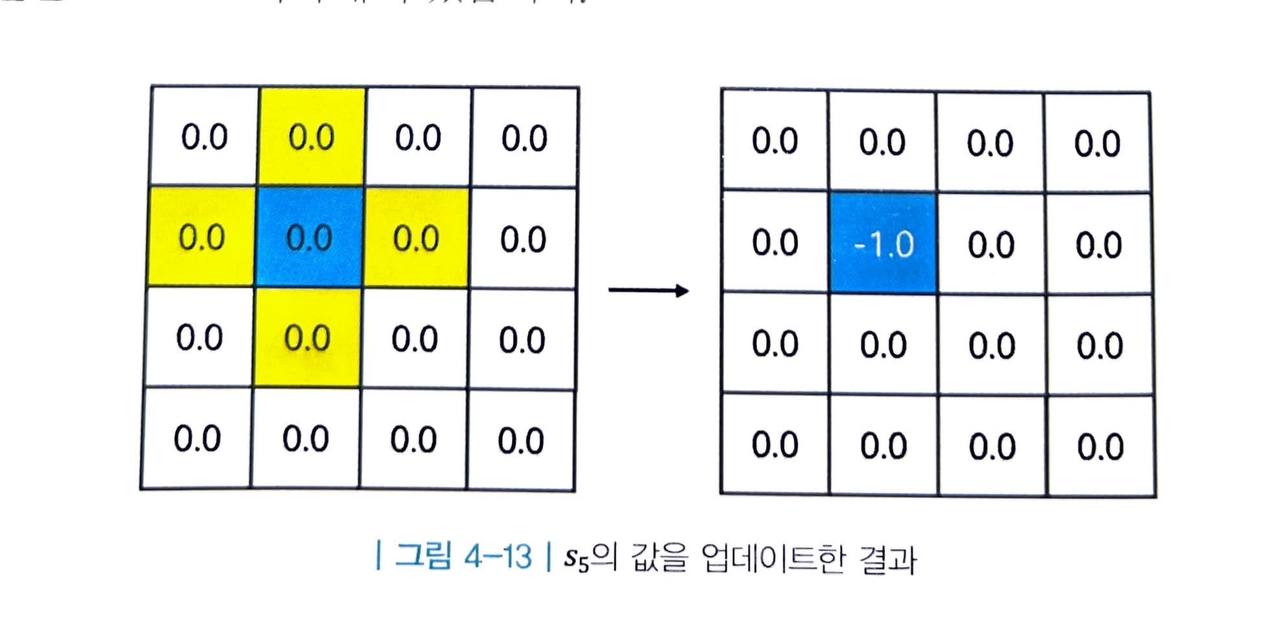
• 이번에도 먼저 한 칸 s5 의 값을 업데이트해 봅니다.

• 벨만 최적 방정식 2단계를 사용하여 s5 의 최적 가치 v*(s)를 계산해보면 다음과 같습니다.

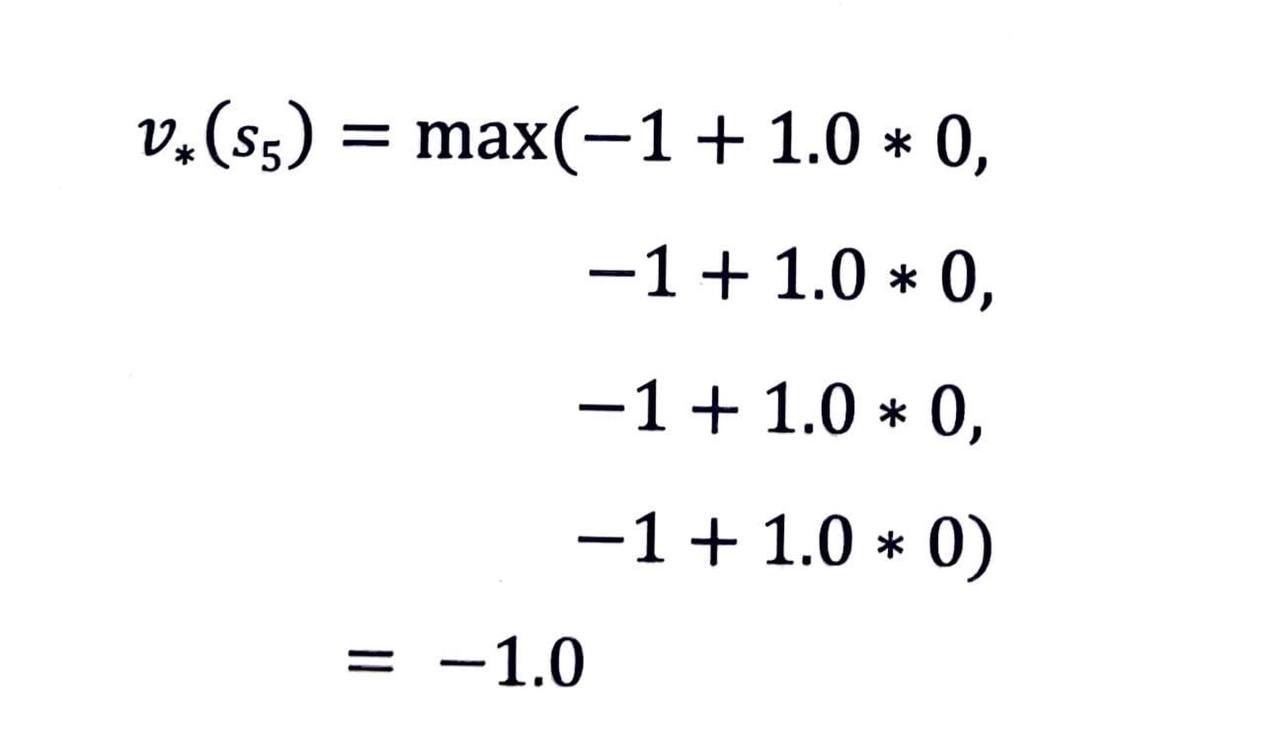
• 테이블의 s5 에 해당하는 값을 -1.0으로 업데이트해 줍니다.

  • 같은 방식을 모든 칸에 대해 적용하면 다음과 그림과 같습니다.

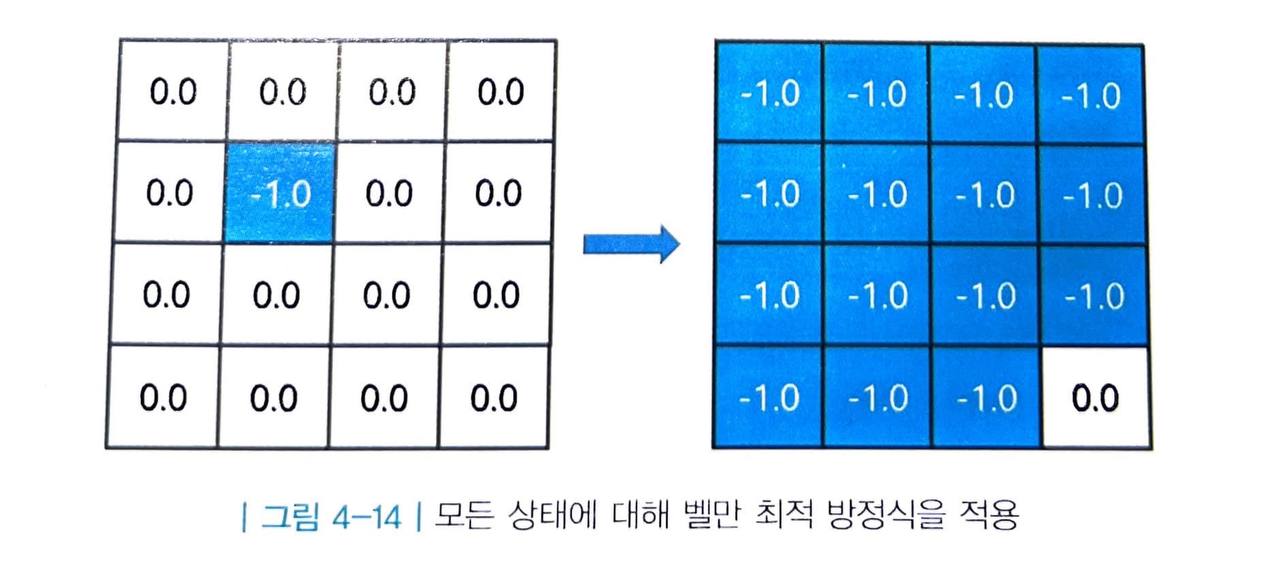
• 같은 방식을 계속해서 반복하면 다음 그림과 같습니다.

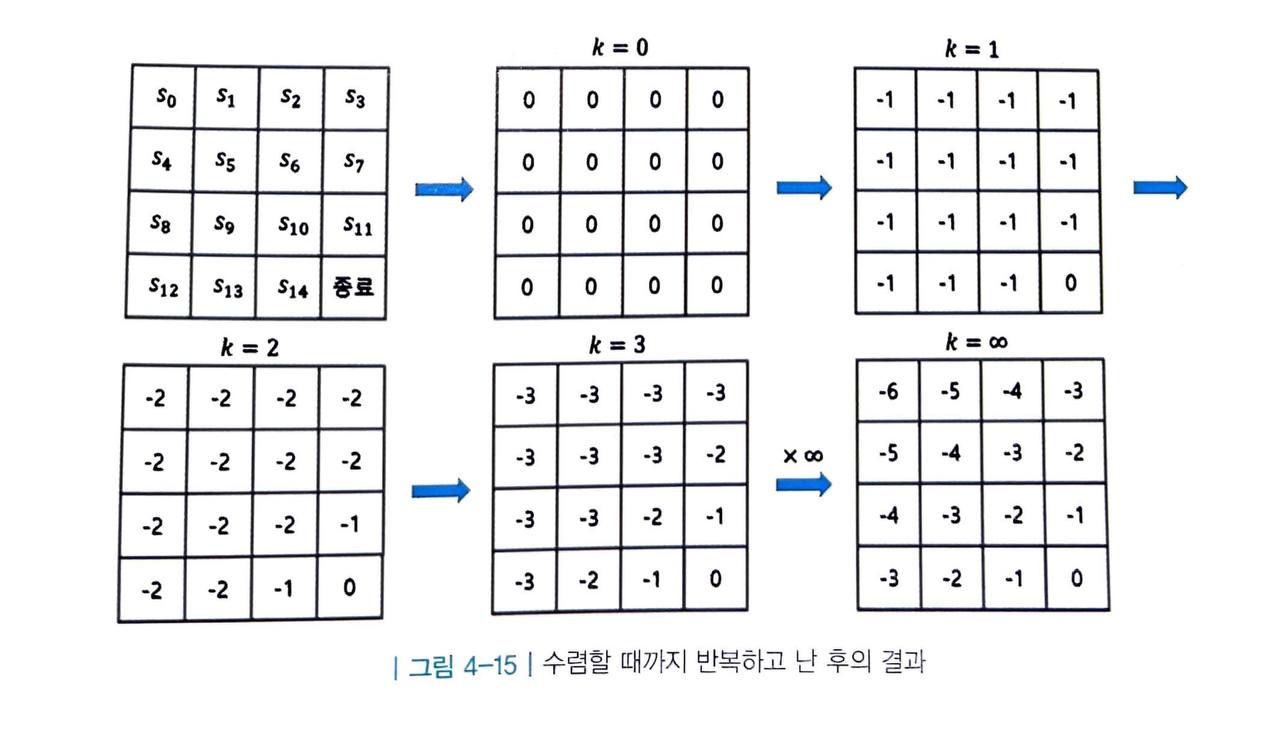
• 테이블의 값들이 수렴하였고, 이 값은 각 상태의 최적 밸류를 의미합니다.

  • 이는 우리의 직관과 일치합니다.

• 위 상황에서는 최적 밸류를 알면 최적 정책을 곧바로 얻을 수 있습니다.

  • 최적 밸류를 높이는 방향으로 그리디 정책을 시행하면 그것이 최적 정책이기 때문입니다.

Reference

• 노승은(2020), 바닥부터 배우는 강화 학습