
벨만 방정식
-
시점 t 에서의 밸류와 시점 t+1 에서의 밸류 사이의 관계를 다루고 있으며 또 가치 함수와 정책 함수 사이의 관계도 다루고 있습니다.
-
벨만 방정식에는 벨만 기대 방정식 과 벨만 최적 방정식 이 있습니다.
재귀 함수
- 벨만 방정식은 기본적으로 재귀적 관계에 대한 식입니다.
- 재귀 함수는 자기 자신을 호출하는 함수를 가리킵니다.
- 다시 말해, 재귀 함수는 자기 자신과의 관계를 이용해 자기 자신을 표현합니다.
- 대표적인 예시로 피보나치 수열이 있습니다.
벨만 기대 방정식
- 벨만 기대 방정식을 편의상 세 단계로 나누겠습니다.

0단계
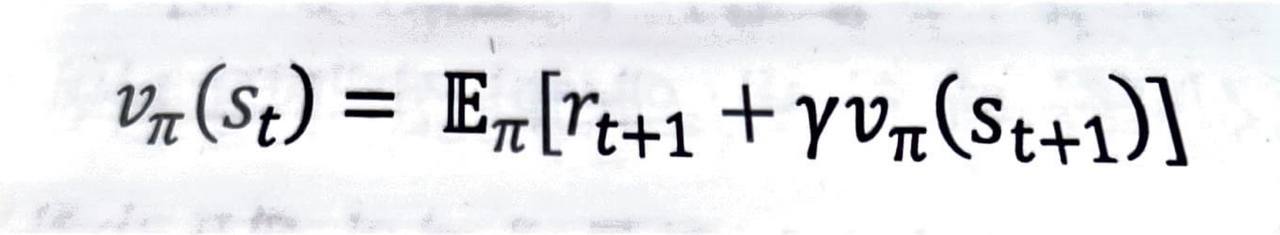
- 이 식은 현재 상태의 밸류와 다음 상태의 밸류 사이 관계를 나타내고 있습니다.
- 위와 같은 관계가 성립하는 이유를 알아보기 위해 vπ 의 정의부터 생각해보겠습니다.
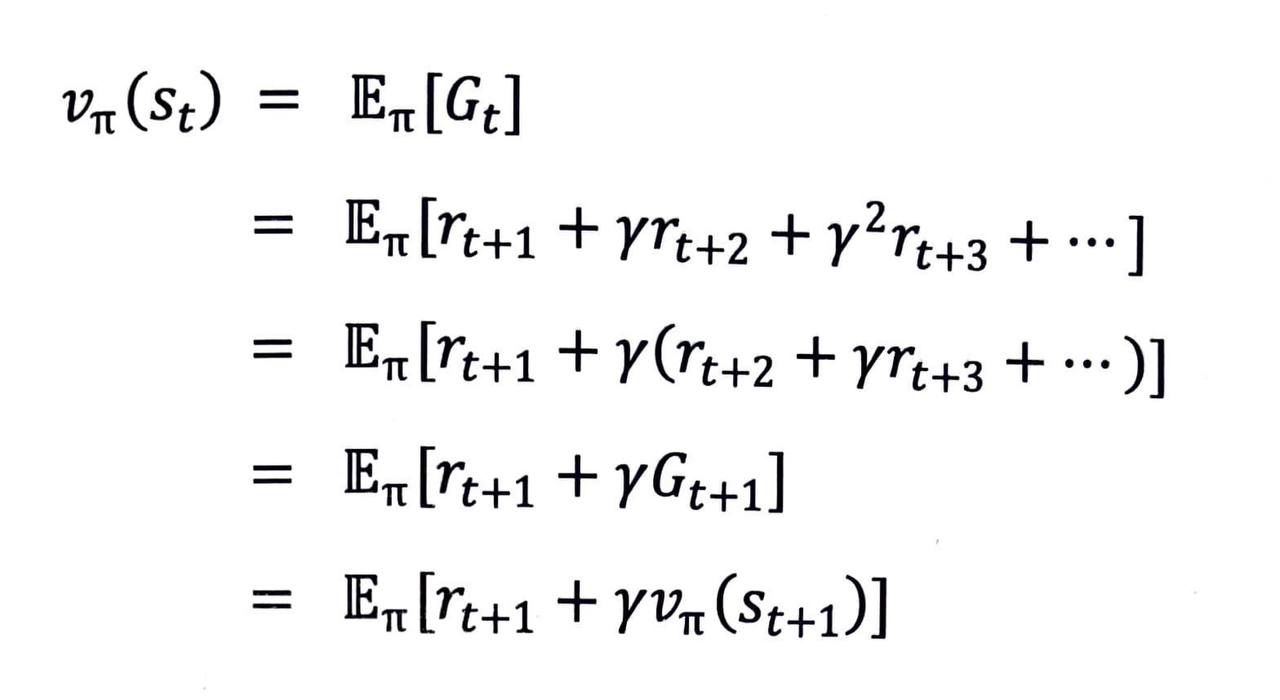
- 수식으로 보면 이와 같이 증명할 수 있습니다.
- 말로 풀어 설명하자면 현재 상태 st의 밸류는 리턴의 기댓값인데 이를 쪼개서 생각해 보자는 것입니다.
- 다시 말해, 리턴이 먼저 한 스텝만큼 진행하여 보상을 받고, 그 다음 상태인 s(t+1) 부터 미래에 받을 보상을 더해줘도 똑같지 않겠느냐 하는 것입니다.
1단계
- 1단계는 액션 밸류 qπ(s, a) 를 이용하여 상태 밸류 vπ(s) 를 표현하는 첫 번째 식과 vπ(s) 를 이용하여 qπ(s, a) 를 표현하는 두 번째 식으로 이루어져 있습니다.
qπ 를 이용해 vπ 계산하기
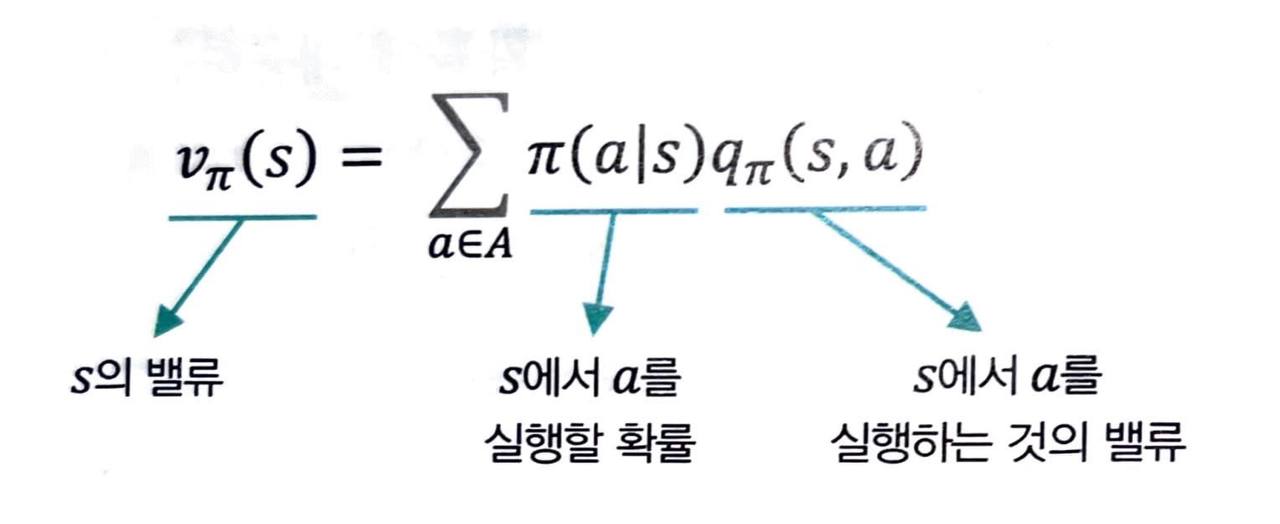
- 위의 식을 이해하기 위해 다음 그림을 참고해 봅시다.
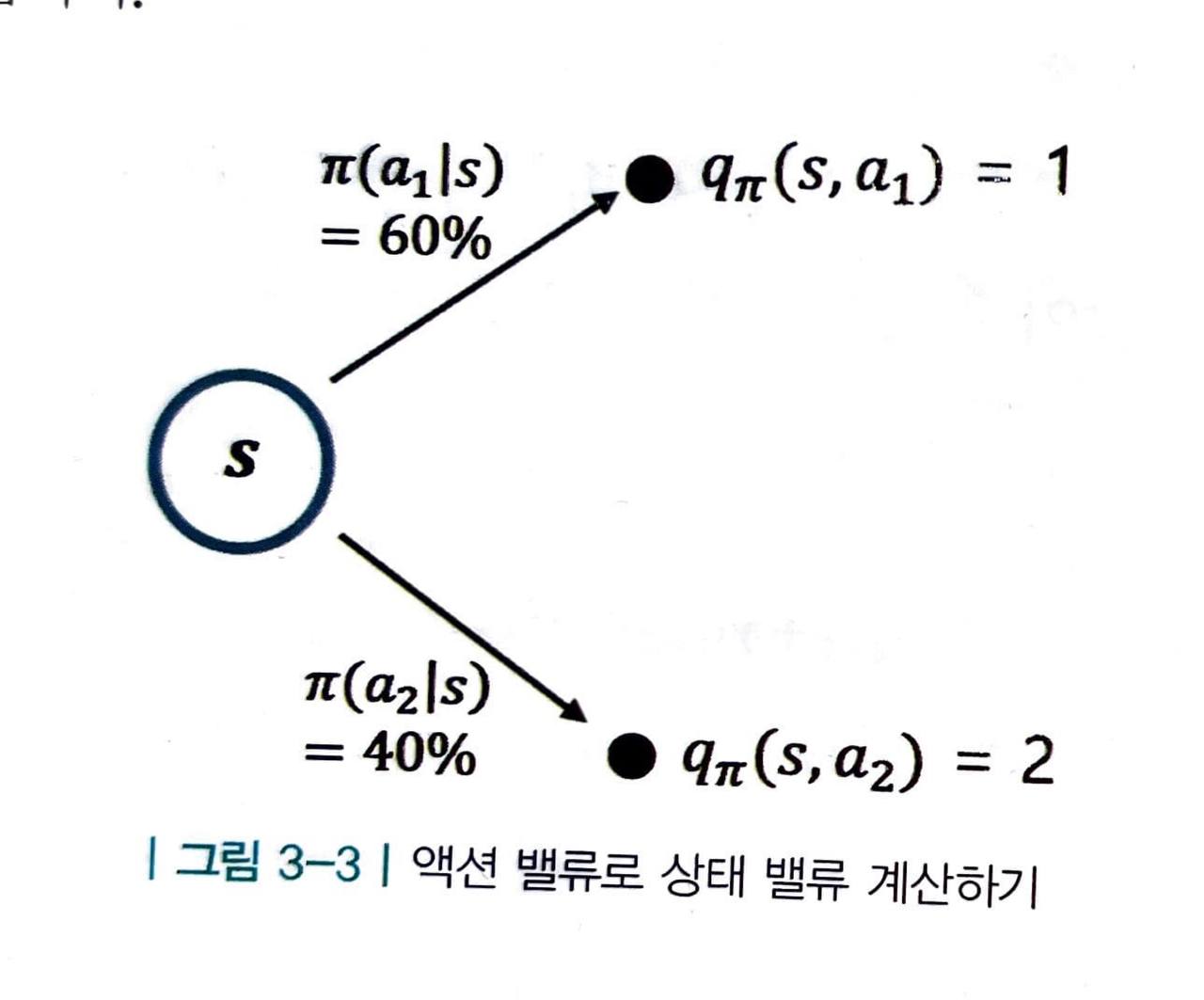
- 위와 같이
- 정책 π 가 두 액션을 선택할 확률을 알고,
- 액션 밸류 q 의 값을 알고 있다면,
s 의 밸류를 구할 수 있습니다.
- 이 때, 정책은 π 로 고정되어 있습니다.
- 이를 식으로 풀어 써보면 다음과 같습니다.
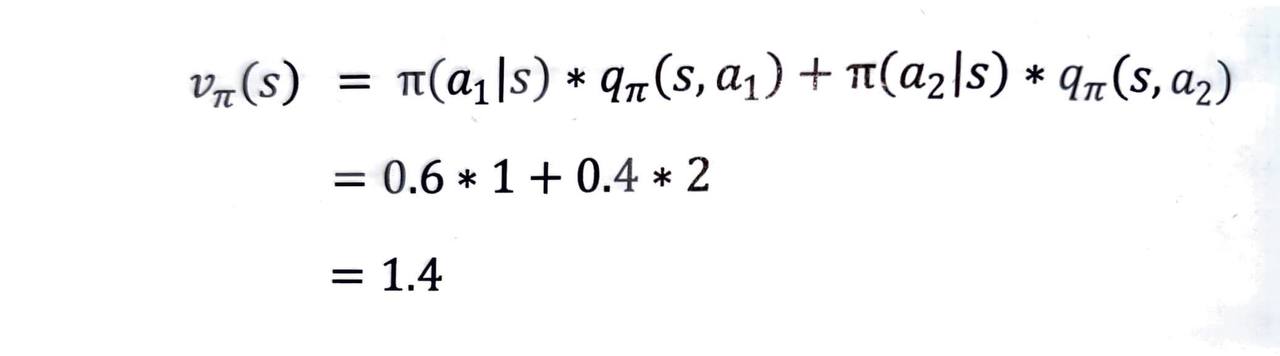
- 정리해보면 어떤 상태에서 선택할 수 있는 모든 액션의 밸류를 알고 있다면, 이를 이용해 해당 상태의 밸류를 계산할 수 있습니다.
- 액션의 밸류에 액션을 선택할 확률을 곱해서 시그마를 이용해 모두 더해주는 방식입니다.
vπ 를 이용해 qπ 계산하기
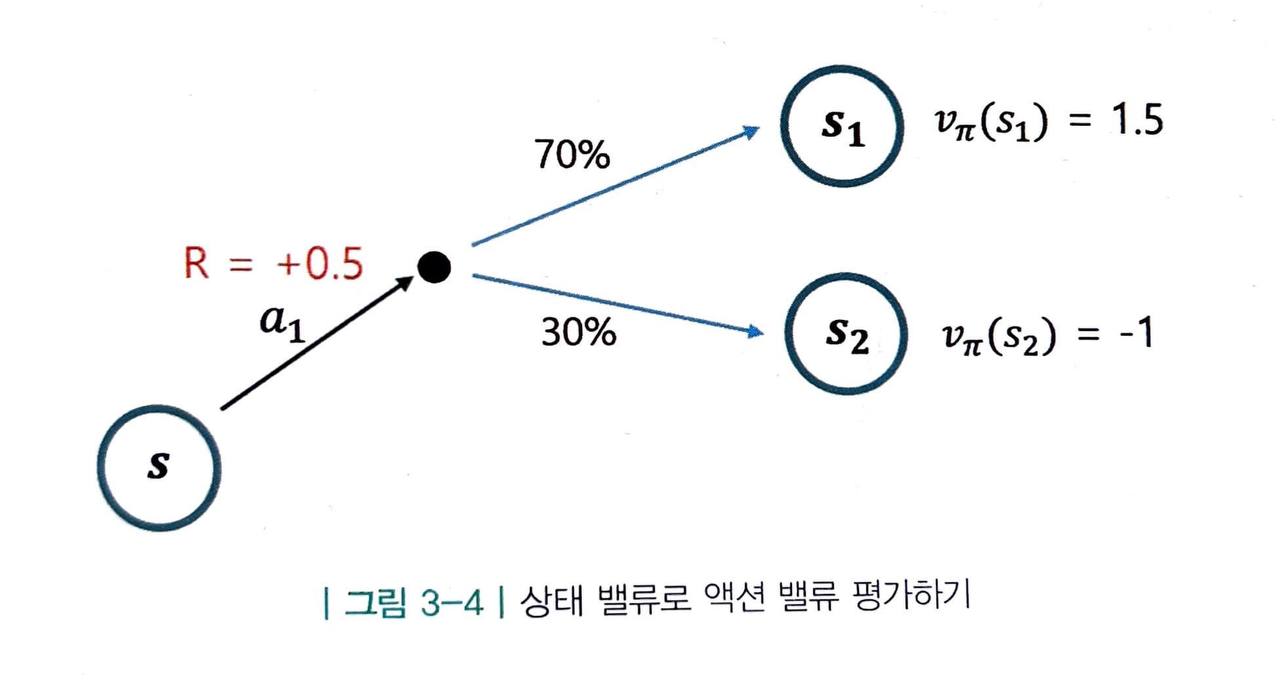
- 이번에는 반대로, 상태의 밸류를 이용해 액션의 밸류를 평가해보겠습니다.
-
위와 같이
- a1 을 선택하자마자 얻는 보상의 값을 알고,
- 액션 a1을 선택하면 다음 상태가 어디가 될지 그 각각에 대한 전이 확률도 알고,
- 각 상태의 밸류 또한 알고 있다면,
-
상태 s 의 밸류를 구할 수 있습니다.
-
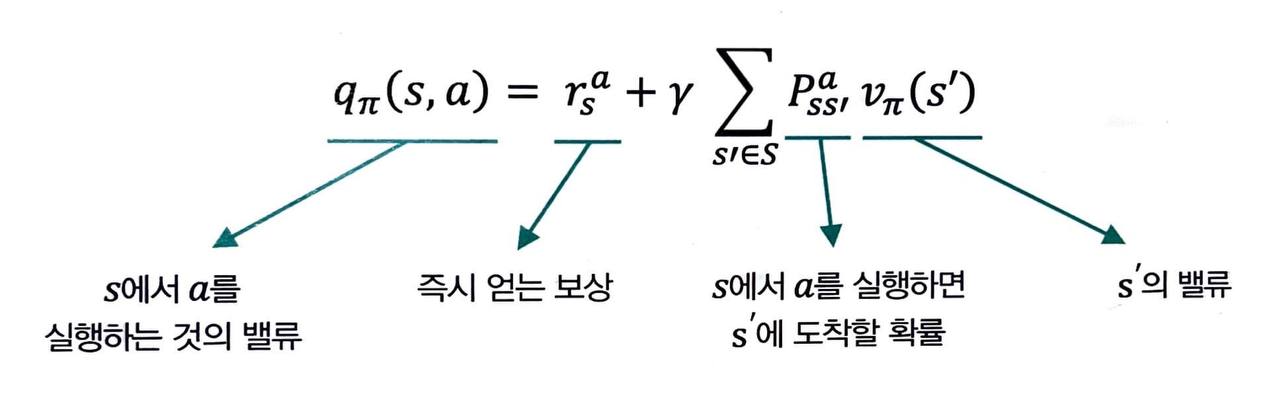
우선 받는 보상을 더해주고, 그 다음에 도달하게 되는 상태의 밸류와 그 확률을 곱해서 더해주면 됩니다. 식으로 표현해보면 다음과 같습니다.
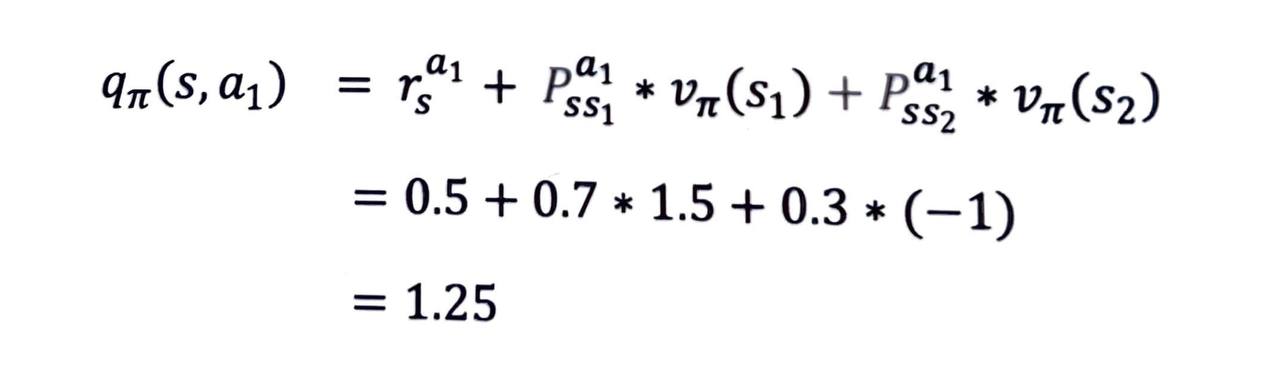
2단계
-
2단계는 앞서 설명한 1단계의 수식들을 대입만 하면 끝입니다.
-
1단계의 qπ 에 대한 식을 vπ 에 대한 식에 대입하면 다음과 같은 결과를 얻습니다.
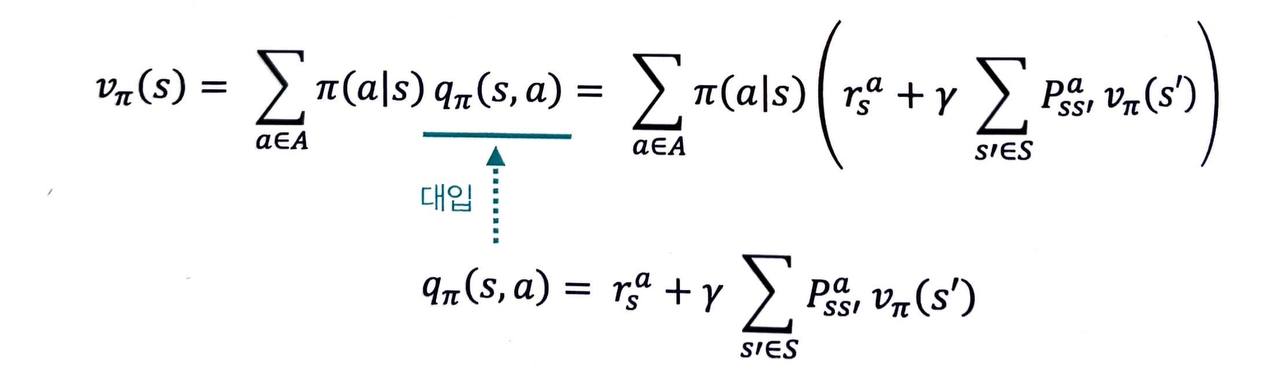
- 반대로 vπ 에 대한 식을 qπ 에 대한 식에 대입하면 다음과 같은 결과를 얻습니다.

- 이렇게 하여 얻은 최종 수식은 각각 다음과 같습니다.
- 바로 벨만 기대 방정식 2단계 수식입니다.
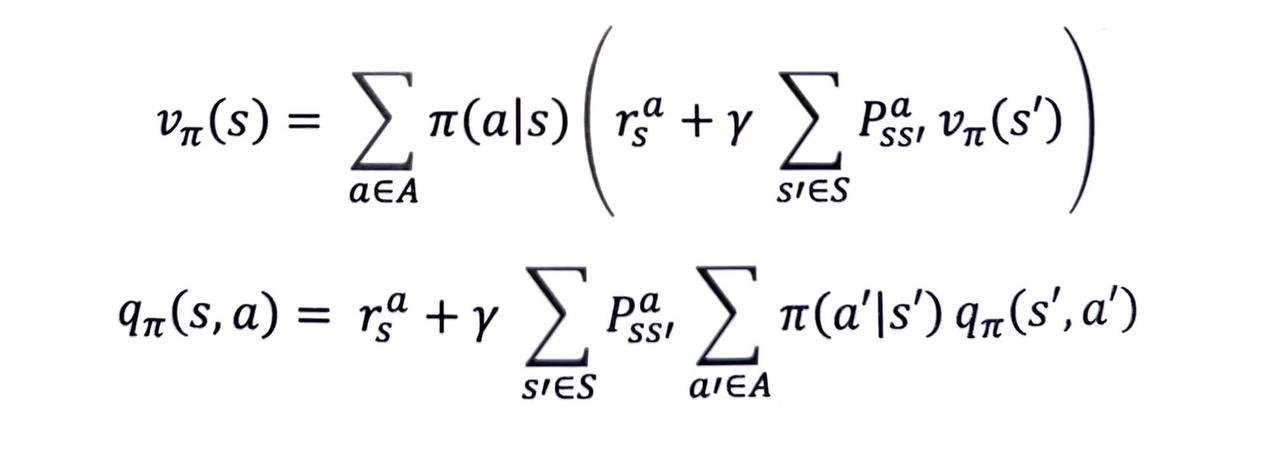
정리
-
그래서 이러한 복잡한 식이 무엇을 위한 수식일까요?
-
최종적으로 얻어진 식 중에서 vπ(s) 에 대한 식을 벨만 기대 방정식 0단계의 식과 나란히 써 보겠습니다.
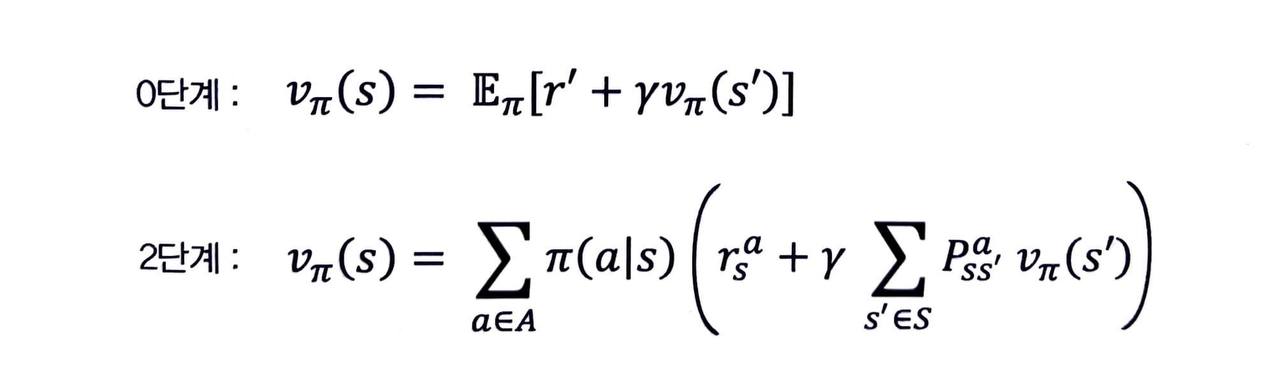
-
0단계 식은 현재 상태의 밸류와 다음 상태의 밸류를 기댓값 연산자를 통해 연결해 놓은 식이었습니다.
- 그래서 그 기댓값을 어떻게 계산하지? 에 대한 대답이 바로 벨만 기대 방정식 2단계 수식이 되는 것입니다.
-
2단계 식을 계산하기 위해서 다음 2가지를 반드시 알아야 합니다.
- 보상 함수 r(s, a) : 각 상태에서 액션을 선택하면 얻는 보상
- 전이 확률 P(s, a, s') : 각 상태에서 액션을 선택하면 다음 상태가 어디가 될지에 관한 확률 분포
-
보상 함수와 전이 확률은 환경의 일부이므로, 이 2가지에 대한 정보를 알 때 "MDP 를 안다" 고 표현합니다.
- 이런 종류의 접근법을 모델 기반 혹은 플래닝 이라고 합니다.
-> 이 때에는 벨만 기대 방정식 중에서 2단계 식을 이용합니다.
- 이런 종류의 접근법을 모델 기반 혹은 플래닝 이라고 합니다.
-
반대로 MDP 에 대한 정보를 모를 때, 경험 을 통해 학습하는 접근법을 모델-프리 접근법이라고 합니다.
-> 이 때에는 벨만 기대 방정식 중에서 0단계를 이용합니다.
벨만 최적 방정식
최적 밸류와 최적 정책
-
벨만 기대 방정식이 vπ(s) 와 qπ(s, a) 에 대한 수식이라면 벨만 최적 방정식은 v*(s) 와 q*(s, a) 에 대한 수식입니다.
- v*(s) 와 q*(s, a) 는 최적 밸류 에 대한 함수입니다.
-
최적 밸류의 정의는 다음과 같습니다.

-
말로 풀어서 설명해보면, 어떤 MDP 가 주어졌을 때 그 MDP 안에 존재하는 모든 π 중에서 가장 좋은 π 를 선택하여 계산한 밸류가 곧 최적 밸류 v*(s) 라는 뜻입니다.
-
만약 상태별로 가장 높은 밸류를 주는 정책이 모두 다르면 어떡할까요?
- 각각의 상태에 대해 서로 다른 정책을 따르는 새로운 정책 π* 를 정의하면 됩니다.
-
정책 π* 를 따르면 모든 상태에 대해 그 어떤 정책보다도 높은 밸류를 얻게 됩니다.
- 이러한 정책 π* 를 최적 정책 이라고 부릅니다.
-
최적의 정책만 정의되고 나면 최적의 밸류, 최적의 액션 밸류는 다음과 같은 등식을 만족합니다.
- 최적의 정책 : π*
- 최적의 밸류 : v*(s) = vπ*(s) (π* 를 따랐을 때의 밸류)
- 최적의 액션 밸류 : q*(s, a) = qπ*(s, a) (π* 를 따랐을 때의 액션 밸류)
다시, 벨만 최적 방정식

0단계
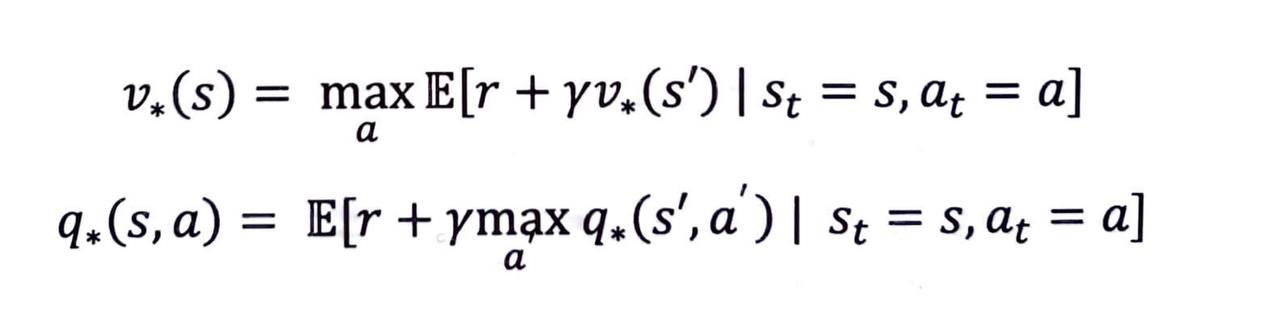
-
이 식은 벨만 기대 방정식의 0단계 수식과 같은 취지의 식입니다.
- 상태 s 에서의 최적 밸류는 일단 한 스텝만큼 진행하여 보상을 받고, 다음 상태인 s' 의 최적 밸류를 더해줘도 똑같지 않겠느냐 하는 것입니다.
-
벨만 기대 방정식 0단계 수식과 비교하여 눈여겨볼 부분은 Eπ 가 E 로 바뀌었다는 점입니다.
- 원래는 주어진 π 가 있어서 π 가 액션을 선택했지만 이제는 할 수 있는 모든 액션들 중에 E[ r+γv*(s') ] 의 값을 가장 크게 하는 액션 a 를 선택해야 하기 때문에 π 의 역할은 없어지게 됩니다.
1단계
- 벨만 기대 방정식과 마찬가지로 1단계는 최적 액션 밸류 q*(s, a) 를 이용하여 최적 상태 밸류 v*(s) 를 표현하는 첫 번째 식과 v*(s) 를 이용하여 q*(s, a) 를 표현하는 두 번째 식으로 이루어져 있습니다.
q* 를 이용해 v* 계산하기
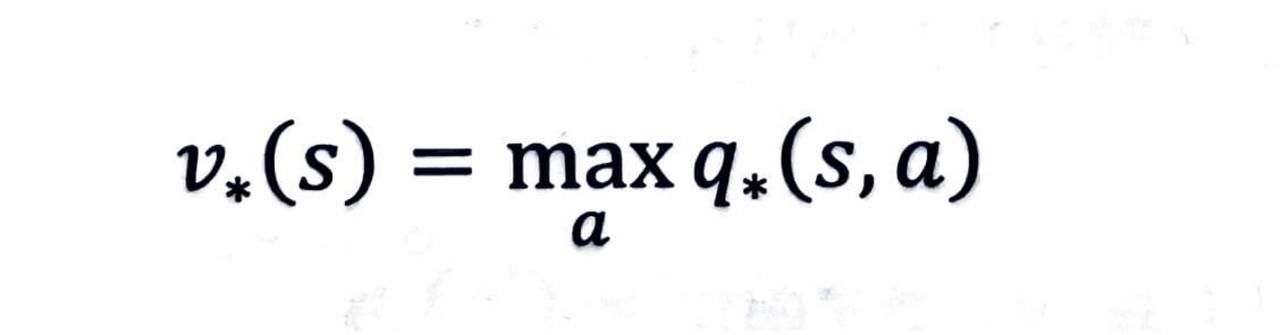
-
상태 s 의 최적 밸류는 s 에서 선택할 수 있는 액션들 중에 밸류가 가장 높은 액션의 밸류와 같다는 뜻입니다.
-
각 액션을 선택할 확률을 고려하지 않아도 되는 이유는 무엇일까요?
- 100퍼 센트의 확률로 최적의 액션 a 를 선택하는 것이 최적의 밸류를 얻게 해주기 때문입니다.
v* 를 이용해 q* 계산하기
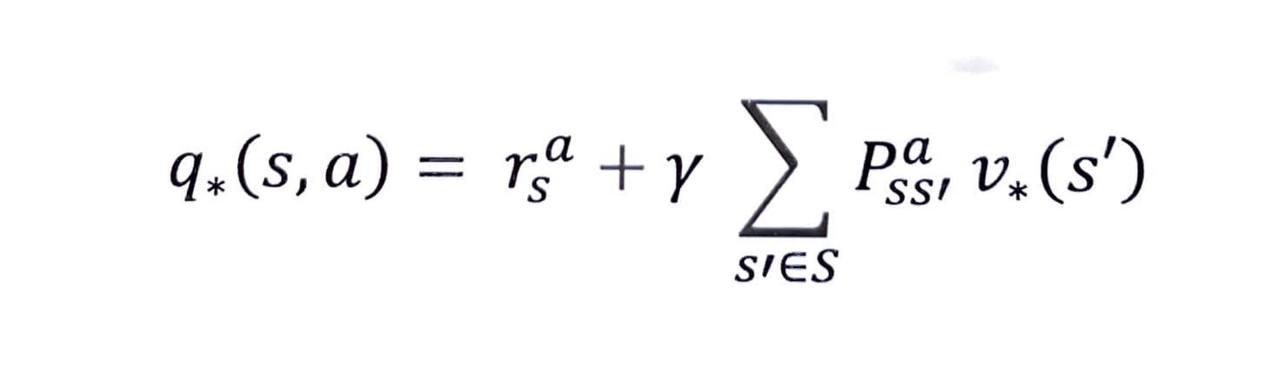
- 이 식은 벨만 기대 방정식의 1단계와 완전히 같은 구조입니다.
- 다만 원래의 π 자리에 * 가 들어갔다는 점만 다릅니다.
2단계
- 2단계 수식 또한 벨만 기대 방정식 때와 마찬가지로 1단계의 수식 2개를 조합하여 만들 수 있습니다.
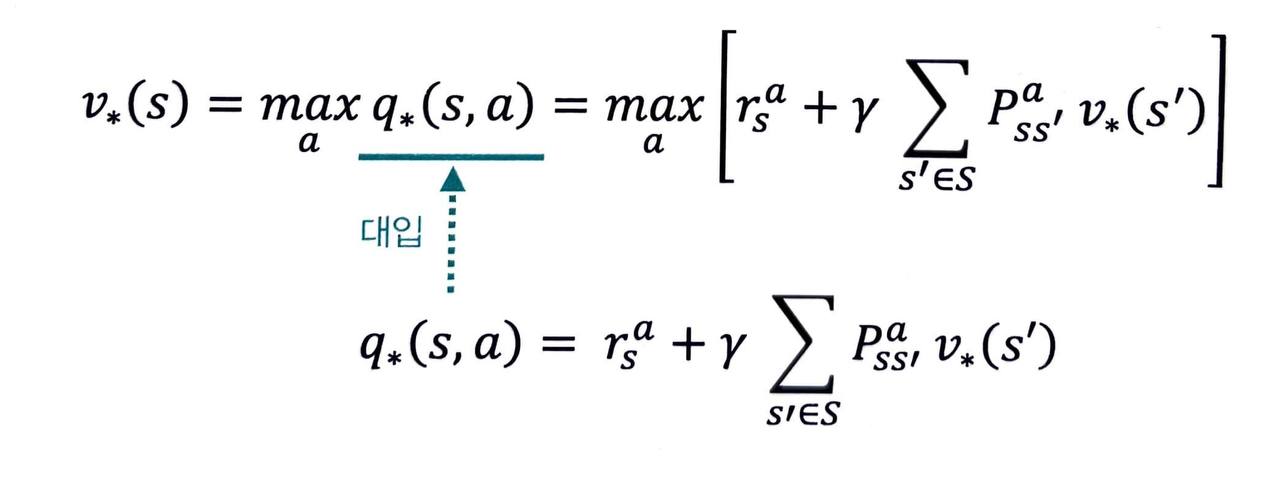
-
이 관계식을 이용해 MDP 를 알 때에 최적 밸류를 구할 수 있습니다.
-
반대로 v*(s) 의 식을 q*(s, a) 의 식에 대입하면 벨만 최적 방정식 2단계의 두 번째 식을 얻게 됩니다.
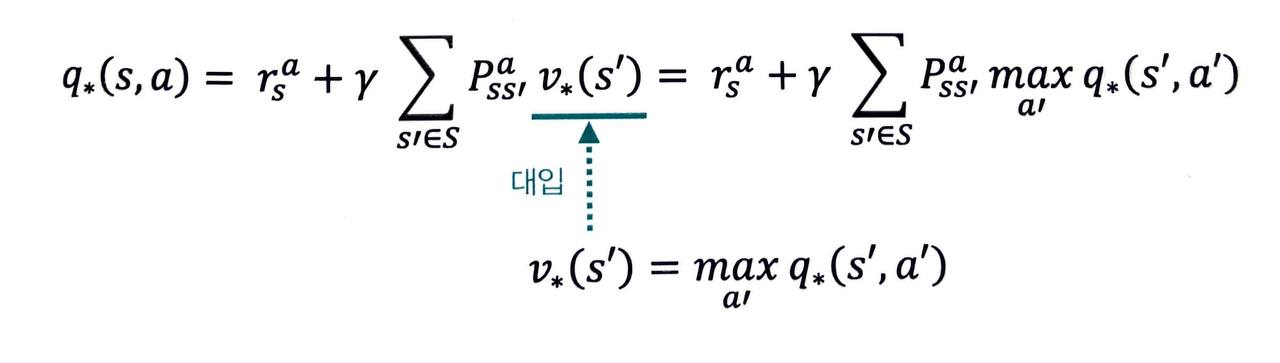
- 최종적으로 얻은 v*(s) 와 q*(s, a) 에 대한 식을 정리하면 다음과 같습니다.
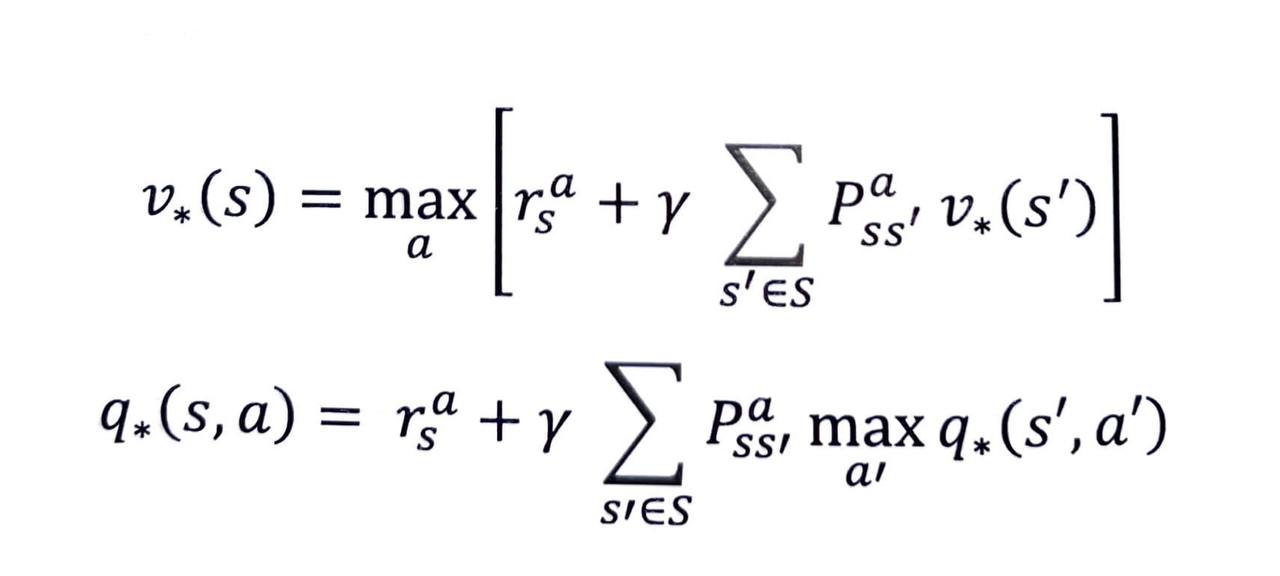
정리
-
무언가 정책 π 가 주어져 있고, π 를 평가하고 싶을 때에는 벨만 기대 방정식을 사용합니다.
-
최적의 밸류를 찾는 일을 할 때에는 벨만 최적 방정식을 사용합니다.
Reference
- 노승은(2020), 바닥부터 배우는 강화 학습
