Diffusion Models?

• 확산 모델은 최근에 새롭게 등장한 생성 모델(Generative Model)의 일종으로, 기존의 생성 모델에 비해 더 우수한 성능과 유용한 특성들로 인해 많은 관심을 받고 있는 모델입니다.

• 이는 Data 로부터 Noise를 조금씩 더해가면서 Data를 완전한 Noise로 만드는 Forward process와 이와 반대로 Noise 로부터 조금씩 복원해가면서 Data를 만들어내는 Reverse process를 활용합니다.

Generative Models?

• 생성 모델은 상대적으로 낮은 차원의 데이터로부터 높은 차원의 데이터를 만들어내는 작업을 합니다 (e.g. 강아지/고양이 레이블 -> 사진, 텍스트 -> 음성).

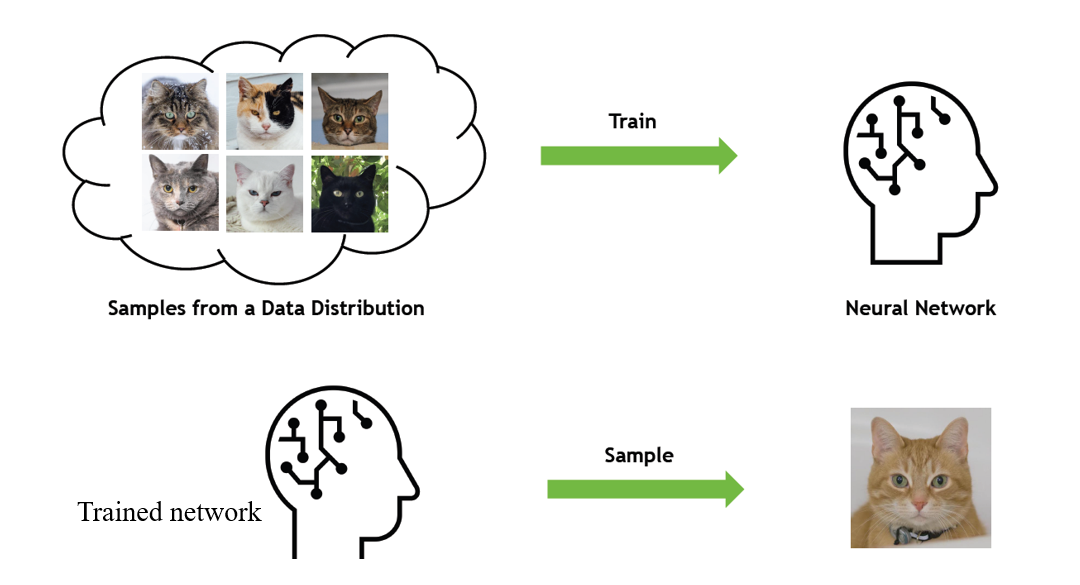
대표적인 생성 모델

VAE

• VAE는 오토 인코더(AE)의 파생형으로, 인코더를 통해 입력 값을 특정 확률 분포 상의 한 점으로 만들고, 디코더를 통해 해당 점으로부터 입력 값을 생성해냅니다. VAE는 명시적인 확률 분포를 모델링 한다는 장점이 있으나, 가능도(likelihood)가 아닌 ELBO를 통한 학습이라는 점에서 다소 아쉬움이 존재합니다. 또한 다른 모델들에 비해 비교적 생성된 결과물의 품질이 떨어진다는 단점이 있습니다.

• 더 자세한 정보 -> VAE

GAN

• 데이터를 생성하는 생성자(generator), 그리고 주어진 데이터가 실제 데이터인지 생성된 데이터인지를 판별하는 판별자(discriminator)를 동시에 학습시키는 방식입니다. 학습 후에는 생성자를 이용하여 원하는 값을 만들게 됩니다. GAN은 묵시적(implicit)으로 확률 분포를 모델링 하기 때문에 모델 구성에 제한이 없으며 생성된 결과물의 품질이 뛰어난 편입니다. 다만 생성자와 판별자가 같이 학습이 되어야 한다는 점, 모드 붕괴 등 학습에 어려움이 있는 것으로 알려져 있습니다.

• 더 자세한 정보 -> GAN

Flow-based models

• 단순한 확률 분포에서 추출된 값에 여러 단계의 변환을 거쳐 복잡한 분포를 만드는 방법입니다 (e.g. 노이즈 데이터 -> 개/고양이 사진). 변환 함수를 파라미터화하여 딥러닝 모델로 학습하는 해당 방법은 명시적으로 정확한 likelihood를 모델링한다는 장점이 있고 생성된 결과물의 품질이 좋습니다. 하지만 변환 함수에 역함수가 존재해야 한다는 제한이 있기 때문에 모델을 만들 때 사용하는 연산자에 제한이 있습니다.

• 더 자세한 정보 -> Flow-based models

다시, Diffusion Models

• 앞서 살펴본 생성 모델들이 하는 일은 노이즈와 실제 사진과의 관계를 간략화하여 나타내는 것입니다.

  • VAE는 인코더와 디코더를 통해, [사진 -> Latent Variable -> 사진] 에서 Latent Variable 를 정규 분포로 만드는 방법을 학습하였고,
  • GAN은 [정규 분포 -> 사진] 의 디코더를 학습하였습니다.
  • Flow-based model은 이를 여러 단계의 가역함수로 나눈 것입니다.

• 확산 모델은 Flow-based model과 비슷합니다. 확산 모델은 초기 상태의 분자들이 시간이 흐름에 따라 흩어지는 것을 나타내는 Langevin dynamics 에서 아이디어를 가져왔습니다.

  • 간단히 말하자면, 특정 사진의 픽셀들이 시간이 지나면서 흩어져서 노이즈로 변하는 것을 수식을 통해 나타낸 것입니다.

• 이 변환은 정방향 변환(forward)과 역방향 변환(reverse)으로 나뉩니다. 정변환은 데이터가 노이즈로 변하는 것이며, 역변환은 노이즈로부터 데이터가 만들어지는 것입니다.

• 확산 모델에서는 역변환 단계를 파라미터화 하여 딥러닝 모델로 학습하고, 학습된 역변환을 통해 노이즈로부터 데이터를 생성합니다. 따라서 확산 모델은 유한한 시간 후에 사진을 생성하도록 학습된 파라미터화 된 마르코프 연쇄(Markov chain) 라고 할 수 있습니다. 또한 확산 확률 모델에서는 학습에 negative log-likelihood의 ELBO 를 사용합니다.

주요 개념

Latent Variable

• 관찰을 통해 얻을 수 있는 확률벡터 x가 있다고 합시다. 확률벡터 x의 분포를 설명하기 위해 나온 것이 Latent Variable 입니다. 기호로는 z를 쓰도록 합시다. x, z 의 관계는 prior 에 의해 묘사됩니다. 여기서 prior 는 현재 가지고 있는 정보를 기초로 하여 정한 초기 확률을 뜻합니다.

• p(z)를 가정해 주고, x는 latent variable 의 상태에 따라 달라진다는 것을 표현하기 위해 p(x|z)도 가정해 줍니다.

• 위와 같이 prior 와 p(x|z)를 가정해주고 시작하면 다음과 같은 설명이 됩니다.

  • 랜덤벡터 x는 보이지 않는 잠재적 변수 z에 의해 확률적으로 결정됩니다.
    -> z는 보이지 않지만 z가 가지는 값에 따라 x가 존재할 수 있는 공간이 달라질 수 있습니다.

Markov Chain

• Definition

  • 마르코프 성질을 가진 이산 확률 과정

• Property

  • 특정 상태의 확률은 오직 과거의 상태에 의존

ELBO (Evidence Lower Bound)

• Evidence : Data 의 log likelihood (로그 우도)

  • 따라서 ELBO 는 말 그대로 Evidence 의 최저점

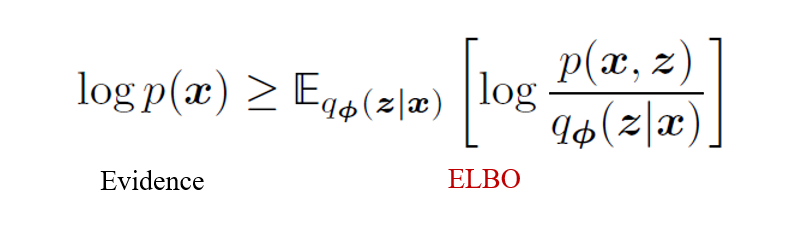
• 앞서, VAE에서는 ELBO를 통해 학습을 한다고 언급하였습니다. 따라서 VAE의 상황을 예로 들겠습니다.

• 우리는 VAE에서 사후 확률 분포(posterior distribution)인 p를 알고 싶은데, 이를 직접 구하는 것은 어려우므로 이에 근사할 수 있는 사후 확률 분포(variational approximation of the posterior distribution)인 q를 찾는 변분 추론을 해야합니다.

• 우리의 최종 목적은 p와 q 분포의 차이를 줄이는 것 인데, 이는 두 확률 분포의 KL Divergence가 작아져야 됨을 뜻합니다.

  • log p(x)의 값이 상수이므로, ELBO가 커지면 KL Divergence 값이 작아지게 됩니다.
    -> 따라서 우리는 ELBO를 Maximize 하면 된다는 결론에 다다르게 됩니다.

Forward Process

• 실제 데이터 분포로 샘플링된 초기 데이터 포인트가 주어지면 Forward 프로세스는 Markov Gaussian diffusion kernel (Markov chain)을 반복적으로 적용하여 분포를 간단하고 다루기 쉬운 분포(Gaussian, Binomial)로 변환합니다.

• 특히, 마르코프 체인의 t번째 단계에서 Diffusion rate βt 를 사용하여 Gaussian noise 를 생성하고 이를 x(t−1)에 추가하며, 이 과정은 분포 q(xt|x(t−1))에서 새로운 latent variable xt를 샘플링하는 것으로 정의됩니다.

Diffusion rate β

• Diffusion rate βt 는 t단계에 어느 정도의 노이즈를 추가할 것인지를 정합니다.

• βt 값의 집합은 알고리즘에 따라 예약되고 학습 전체에서 고정됩니다.

다시, Forward Process

• Forward process에 대한 조건부 분포는 가우스 분포로 공식화됩니다.

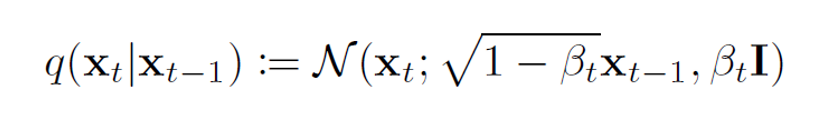
• xt를 생성하기 위해 Gaussian noise 를 추가하는 것은 샘플링 형태로 공식화됩니다.

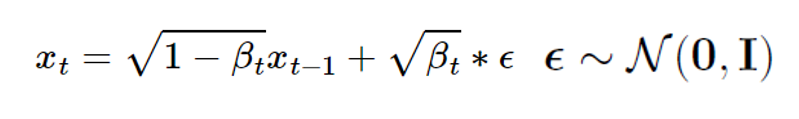
• Reparametrization trick 을 사용하면 임의 평균 μ 및 분산이 σ^2인 정규 분포 x ~ N(x ; μ, σ^2)의 표본을 다음과 같이 다시 작성할 수 있습니다.

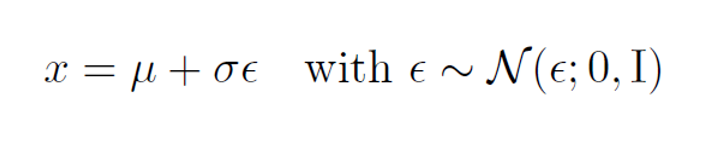
• 이 공식은 평균이 0에서 목표 평균 μ까지 이동하고 분산이 목표 분산 σ^2로 늘어나는 표준 Gaussian(이 중 ε는 샘플)으로 해석될 수 있습니다.

Reparametrization trick

• Backpropagation 과정에서 확률적 샘플링 절차에 의해 생성된 값에 대해 손실이 계산될 때 gradient flow가 발생하지 않습니다.

• Reparametrization trick 은 랜덤 변수를 노이즈 변수의 결정론적 함수로 다시 작성하므로 경사하강법을 통해 비확률적 항을 최적화할 수 있습니다.

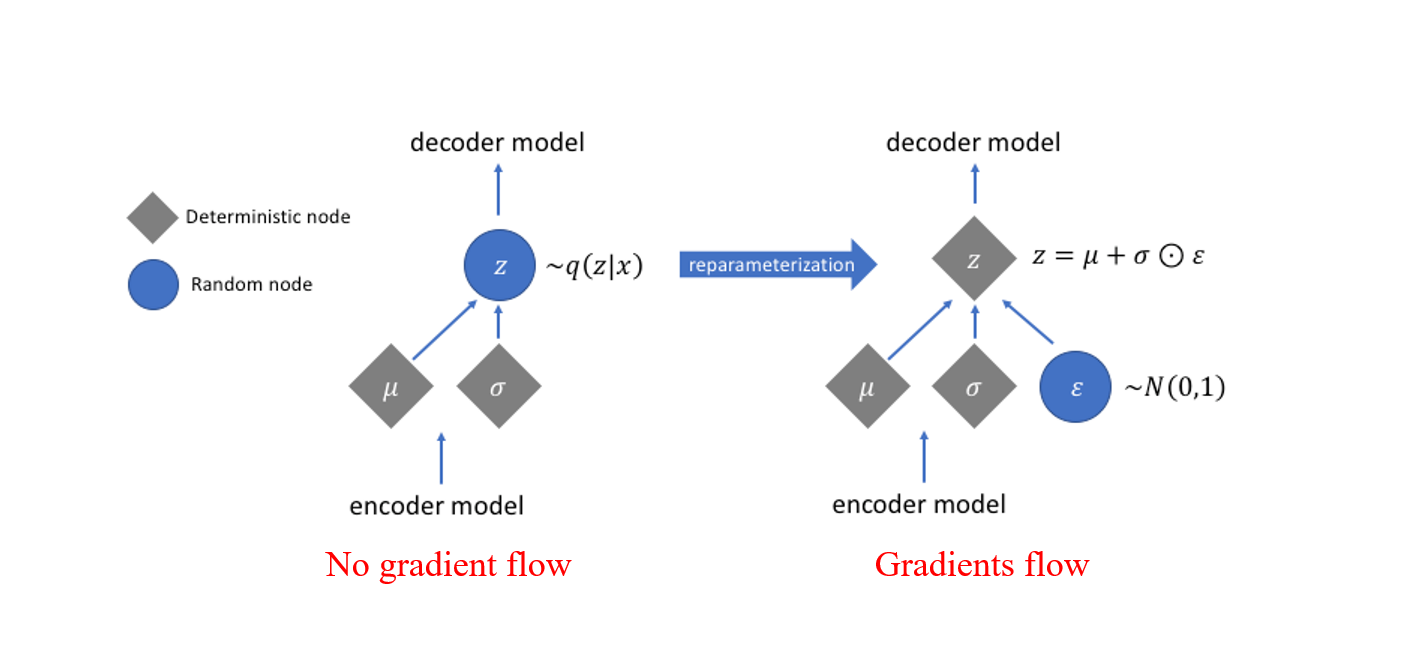
• 한 마디로, stochastic node를 stochastic한 부분과 deterministic한 부분으로 분해시켜서 deterministic한 부분으로 backpropagation을 흐르게 하자는게 핵심

다시, Forward Process

• Gaussian noise를 지속적으로 추가하면 q(xt)의 분포가 표준 Gaussian 으로 수렴합니다.

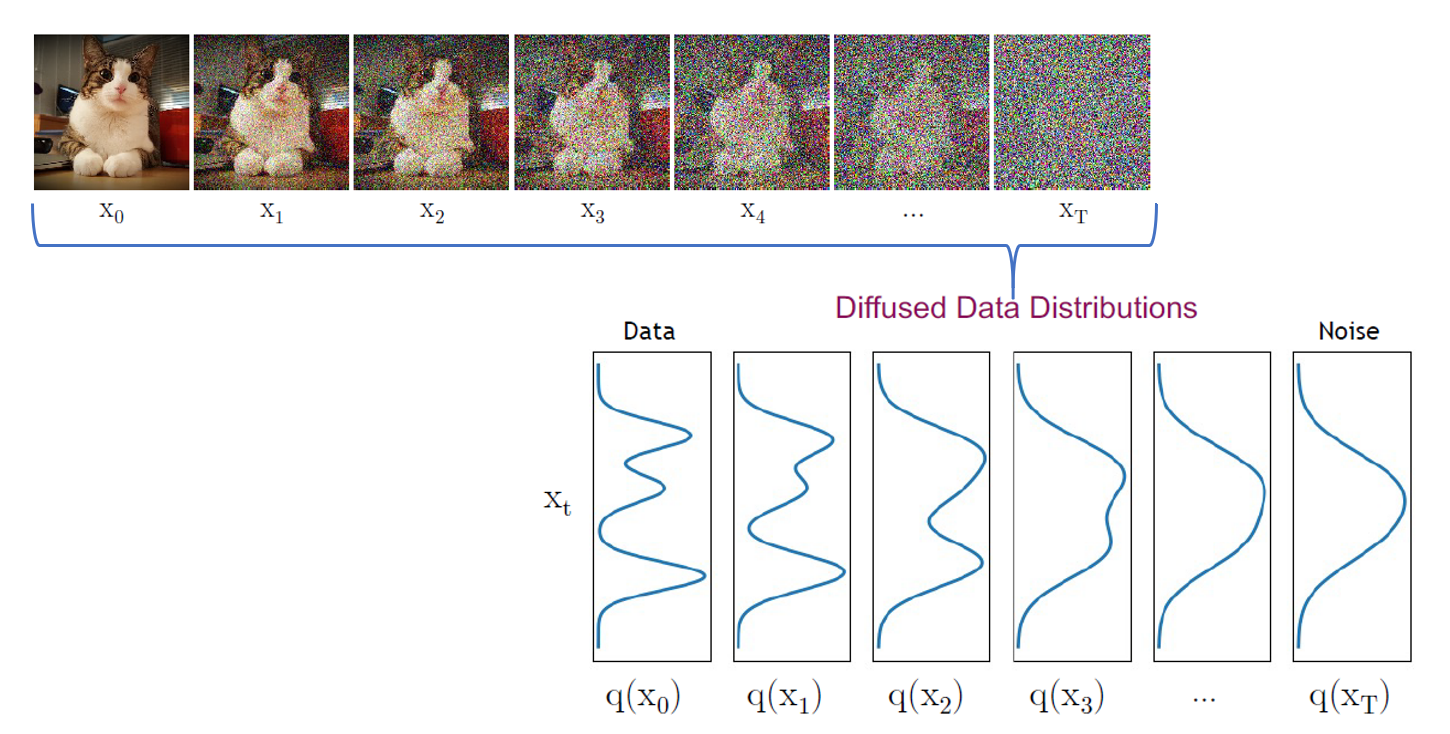
Reverse Process

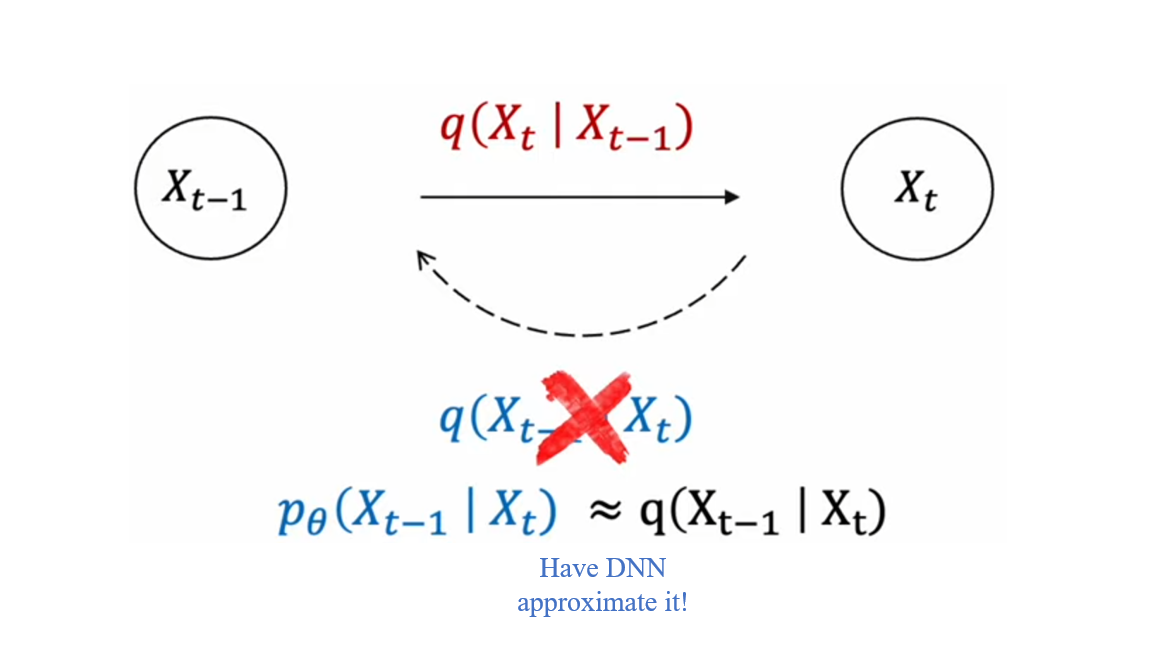
• 역 조건부 분포 q(x(t−1) | xt) 를 학습하면, 정규 분포 N(0,1)에서 xt를 샘플링하고, 역 프로세스를 실행하며, q(x0)에서 샘플을 수집하여 원래 데이터 분포에서 새로운 데이터 포인트를 생성할 수 있습니다.

  • 그러나 q(x(t−1) | xt) 의 통계적 추정치를 구하는 데에 데이터 분포와 관련된 계산이 필요하기 때문에 거의 불가능에 가깝습니다.

How? - Intuition from Feller

• 연속적인 Gaussian diffusion (충분히 작은 β)의 경우, 확산 과정의 Reverse 과정은 Forward 과정과 동일한 기능적 형태를 갖는다는 것이 입증되었습니다.

  • 1949년, Feller에 의해 입증

• 즉, 확산 속도 βt가 충분히 작을 때, q(xt | x(t−1))가 Gaussian 분포를 따르는 경우, q(x(t−1) | xt)도 Gaussian 분포를 따르게 됩니다.

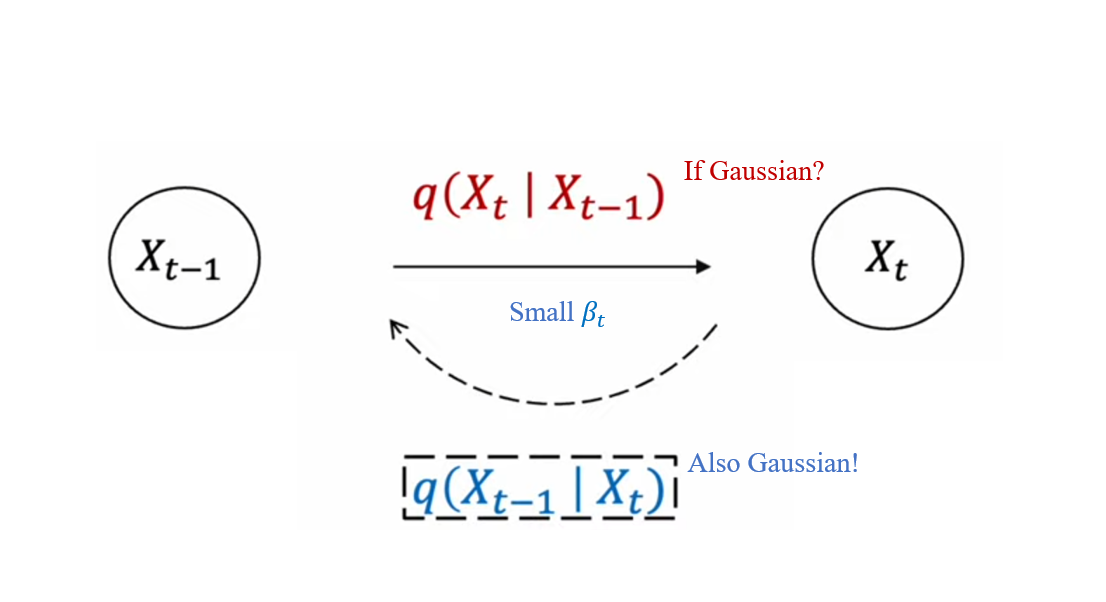
DNN

• 이제 목표 분포가 Gaussian을 따른다는 것을 알고 있지만 이를 어떻게 공식화할지에 대해서는 알 수 없습니다.

  • Deep Neural Network (DNN) 를 사용하게 됩니다.

• 앞서 언급했지만, 확산 모델의 궁극적인 목표는 p와 q의 차이를 줄이는 것, 즉 q에 근사하는 p를 학습시키는 것입니다.

  • 이 학습 과정에 DNN을 도입한다는 것이 Reverse process의 핵심입니다.

• 더 자세한 정보 -> Introduction to Diffusion Models

Evaluations

• 생성된 latents 은 해석할 수 없습니다.

  • VAE는 인코더의 최적화를 통해 구조화된 latent space 를 학습할 수 있는 반면, 확산 모델에서는 각 단계의 인코더가 이미 선형 Gaussian 모델로 제공되어 유연하게 최적화할 수 없습니다.
  • 따라서 중간 단계의 latents 는 원본 입력의 노이즈가 있는 버전으로만 제한됩니다.

• 샘플링은 여러 노이즈 제거 단계를 실행해야 하므로 비용이 많이 드는 절차입니다.

  • 제한 사항 중 하나는 최종 latent 가 완전히 Gaussian noise 임을 보장하기 위해 매우 많은 시간 단계 T가 선택된다는 것입니다. 샘플링하는 동안 샘플을 생성하기 위해 이러한 모든 시간 단계를 반복해야 합니다.

• 확산 모델의 성공은 생성 모델로서의 계층적 VAE의 힘을 강조합니다.

  • 이는 복잡한 인코더와 의미 있는 latent space 를 잠재적으로 학습할 수 있는 일반적이고 심층적인 HVAE의 경우, 추가 성능 향상을 달성할 수 있음을 시사합니다.

Reference

• 생성 모델의 새로운 흐름 확산 모델(Diffusion model)에 관하여
• What are Diffusion Models?
• Diffusion model 설명 (Diffusion model이란? Diffusion model 증명)
• [머신러닝,딥러닝]Latent Variable(잠재변수) 이란?
• Markov Chain 마르코프 체인
• VAE 계열 모델의 ELBO(Evidence Lower Bound) 분석
• Introduction to Diffusion Models for Machine Learning