About the Graph
What is Graph?
-
그래프는 점들과 그 점들을 잇는 선으로 이루어진 데이터 구조입니다. 관계나 상호작용을 나타내는 데이터를 분석할 때 주로 쓰입니다.
- 대표적인 예 : 페이스북 친구 관계, 유튜브, 넷플릭스 등의 유저-영상 감상 여부
-
G = (V, E) 로 나타내며 V 는 꼭짓점(vertex) 의 집합, E 는 에지(edge) 의 집합입니다.
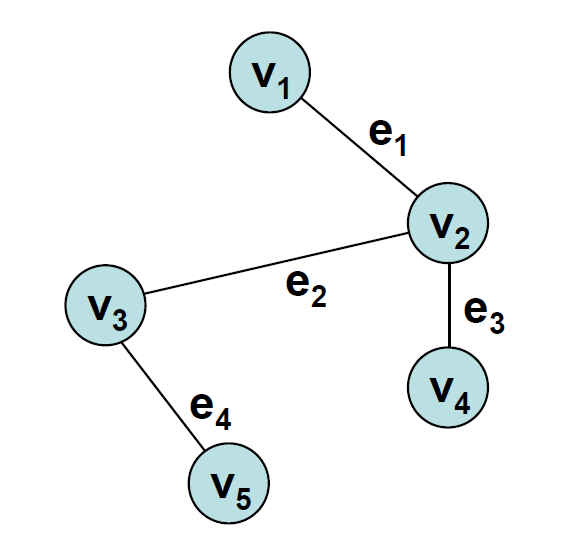
- 에지에는 방향이 있을 수도 있고 없을 수도 있는데, 그래프의 모든 에지에 방향이 존재한다면 이를 유향 그래프(directed graph), 방향이 없는 경우에는 무향 그래프(undirected graph)라고 부릅니다.
Adjacency matrix (인접 행렬)
- 인접 행렬은 그래프에서 정점이 어떤 간선으로 연결되었는지를 나타내는 행렬입니다. 정점 n 개의 그래프에 대해서 n * n 행렬을 이용합니다.
- 이때 정점끼리 연결되어 있다면 행렬의 값을 1로, 연결되어있지 않다면 행렬의 값을 0으로 이용합니다.

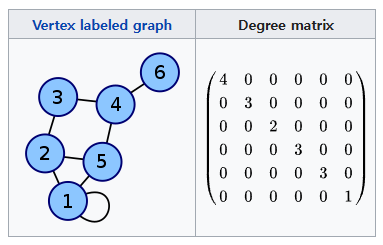
Degree matrix (차수 행렬)
- 무방향 그래프의 차수 행렬은 각 꼭짓점의 차수, 즉 각 꼭짓점에 연결된 간선 수에 대한 정보를 포함하는 대각 행렬입니다.
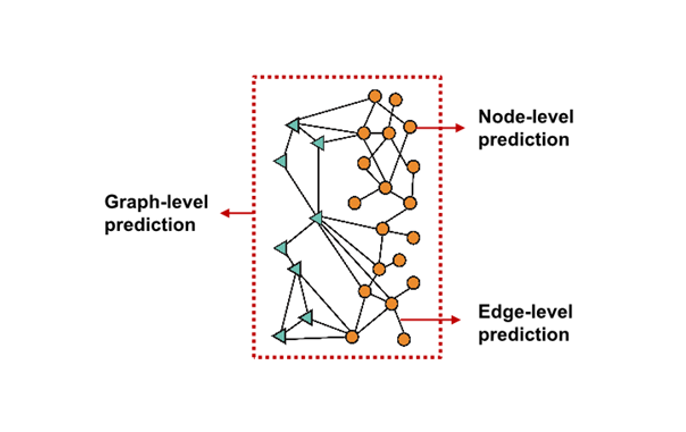
Graph tasks
- Node Level : 각 Node 의 feature 를 예측
- Edge Level : Node 간의 관계(Edge) 를 예측
- Graph Level : Graph 전체를 예측
Why Graph?
-
CNN 은 혁명적인 Neural Network 였지만, Euclidean data 만을 input 으로 받았기 때문에, Non - Euclidean data 로 학습을 할 수 없었습니다.
- 이에 따라 Non - Euclidean data 를 학습할 수 있는 방법으로 Graph 가 제시되었습니다.
-
당연하게도, Graph 는 Euclidean Space 에 있지 않습니다.
- 이는 우리에게 익숙한 좌표계로 표현할 수 없다는 것을 의미하지만, Non - Euclidean Space 에 있는 무언가를 그래프로 표현할 수 있다고도 볼 수 있습니다.
Euclidean Space
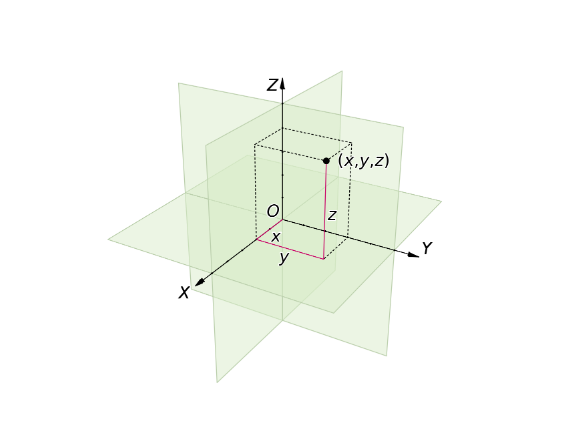
- 평면과 공간을 거리와 길이와 각도, 좌표계를 도입하여, 임의 차원의 공간으로 확장한 것을 말합니다. 이는 표준적인 유한 차원, 실수, 내적 공간입니다.
Non - Euclidean Space
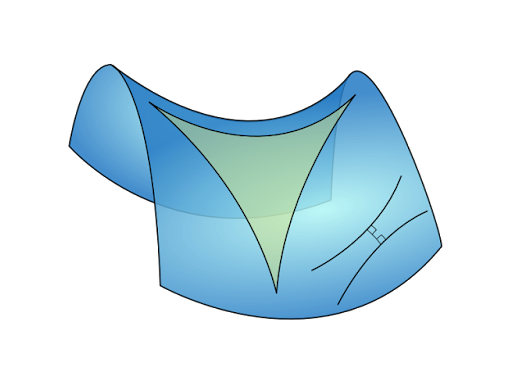
- 평면이 아닌 곡면의 세계에서 점, 선, 면을 설명하는 공간입니다.
The Rise of GNN (Graph Neural Network)
-
앞서 말했던 것처럼, Non - Euclidean data 를 이용해 학습을 하기 위해 Graph 를 사용한 Neural Network, GNN 이라는 개념이 등장하였습니다.
- GNN 은 이름에서도 알 수 있듯이 그래프에 직접 적용할 수 있는 신경망입니다.
-
GNN의 핵심은 점이 이웃과의 연결에 의해 정의된다는 것입니다.
- 만약 어떤 점이 이웃과의 연결을 다 끊으면 그 점은 고립되고 아무 의미를 갖지 않게 됩니다.
- 즉, 노드의 이웃과 이웃에 대한 연결이 노드의 개념을 정의합니다.
-
이를 염두하고, 모든 점(node)이 각각의 특징을 설명하는 어떤 상태(state)로 표현되어 있다고 생각해봅시다.
- 우리는 output 을 만들기 위해서 node state 를 사용합니다.
-
GNN은 주로 연결 관계와 이웃들의 상태를 이용하여 각 점의 상태를 업데이트(학습)하고 마지막 상태를 통해 예측 업무를 수행합니다.
- 일반적으로 마지막 상태를 ‘node embedding’이라고 부릅니다.
-
간단히 말해서, GNN 은 임의의 구조의 그래프 G 가 들어왔을 때 이를 Representation 으로 표현해야 합니다.
- 즉, F(G) = embedding 으로 변환할 수 있는 함수 F를 찾는 것이 GNN 의 목표입니다.
Recurrent Graph Neural Network
-
Recurrent Graph Neural Network 는 GNN의 시초로서 의미가 있습니다. 이는 고수준의 node representation 을 추출하기 위해 노드들의 파라미터들을 재귀적으로 적용합니다.
-
GNN과 다른 점은, GGNN 에서 BPTT(Back Propagation Through Time)을 사용하여 모델을 학습시킨다는 점입니다.
- 이는 큰 그래프에서는 문제가 될 수도 있는데, GGNN 이 모든 노드에 대해 재귀 함수를 여러번 실행하려면 모든 노드의 중간 상태들이 전부 메모리에 저장되어야 하기 때문입니다.
-
Recurrent 모델은 그래프를 탐색하는 가장 직관적인 방법에서 떠올린 모델로서 의미를 갖습니다.
- 이 탐색 과정에서 얻는 결과들이 바로 hidden state가 되고, 이 hidden state 가 모여 결국 그래프의 특성을 결정짓게 되는 방식입니다.
-
하지만 마찬가지로 가장 문제가 되는 부분도 역시 recurrent 부분입니다.
- 이 부분의 연산이 너무 비효율적입니다. 이러한 재귀 연산의 연산량만큼 그 결과가 가치가 있지 않습니다.
- 다른 네트워크로 재귀 없이 병렬 계산하여도 결국 좋은 결과들을 얻을 수 있었고, 재귀 방식은 그 재귀의 깊이만큼 의미를 가지지 못했습니다.
Graph Convolution Network
- Graph 를 Euclidean space 로 보내기 위해 Convolution 연산을 사용합니다.
Convolution
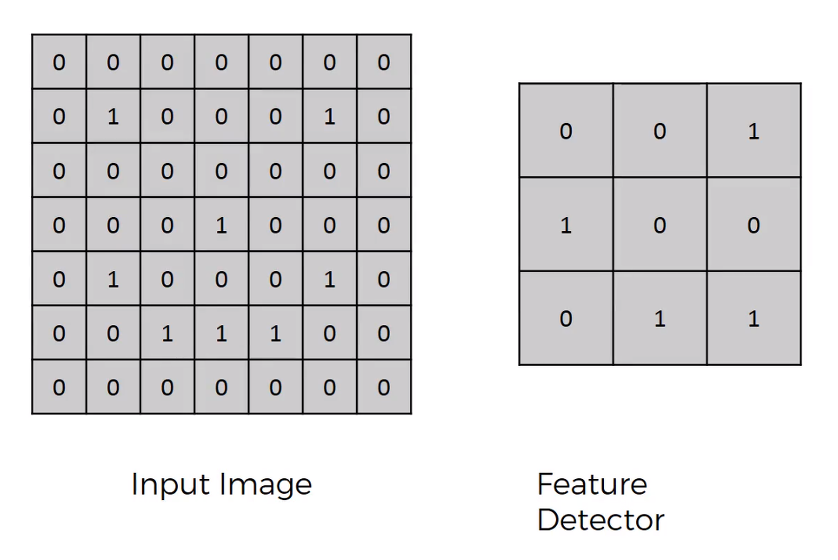
- 위와 같이 어떤 입력 이미지가 들어왔을 때, 여기서 Feature를 감지할 Detector가 존재합니다.
- Detector 를 Kernel 이나 Filter 라고도 표현할 수 있는데, 말 그대로 Detector 가 Input Image 의 모든 영역을 훑으면서 특정 Feature를 뽑게 됩니다.
- 이를 바탕으로 해당 입력에 대한 Feature Map 을 그리게 되는 것입니다.
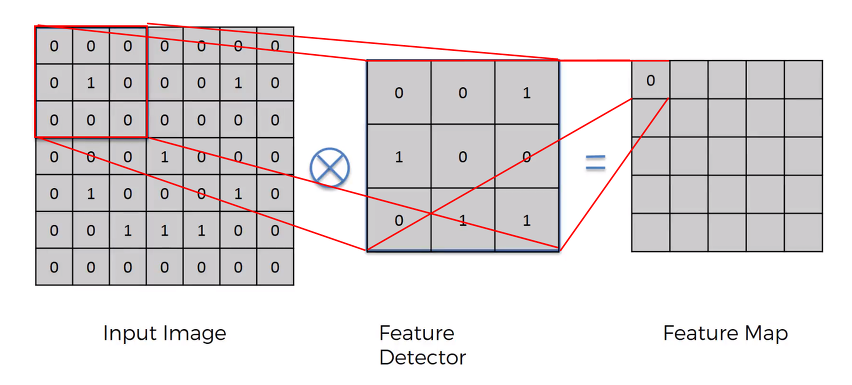
- 이때 Input Image 의 pixel 과 Feature Detector 의 각 kernel 을 곱한 결과를 합하게 되고, 그 결과가 Feature Map 의 하나를 채우게 됩니다.
- 이 과정을 Feature Detector 가 입력 이미지를 모두 훑을 때까지 계속합니다.
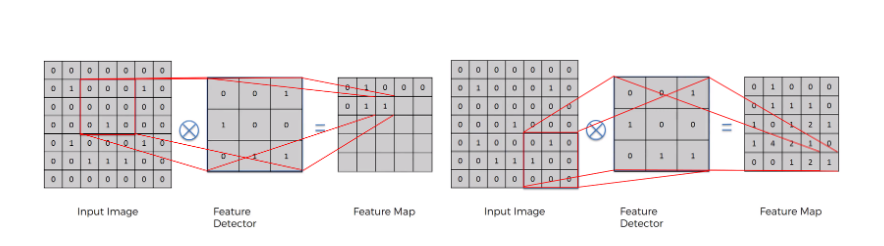
-
이렇게 Feature Map을 만들고, 원래 입력 이미지와 크기를 비교해보면 원래의 7x7 이미지가 5x5 이미지로 작아진 것을 알 수 있습니다.
- 다시 말해 pixel 별로 비교해도 49회 걸리던 일이 25회만 비교하면 되는 것입니다.
-
이로 인해 이미지 비교시 속도라는 이점을 얻을 수 있는게 Convolution 연산의 특징입니다.
- 물론 속도가 빠른만큼 원래 정보가 소실된다는 점도 있긴 하나, 우리의 목적이 모든 pixel을 비교하는 게 아닌, 이미지의 특징을 뽑아내는 것이므로 이런 과정이 필요합니다.
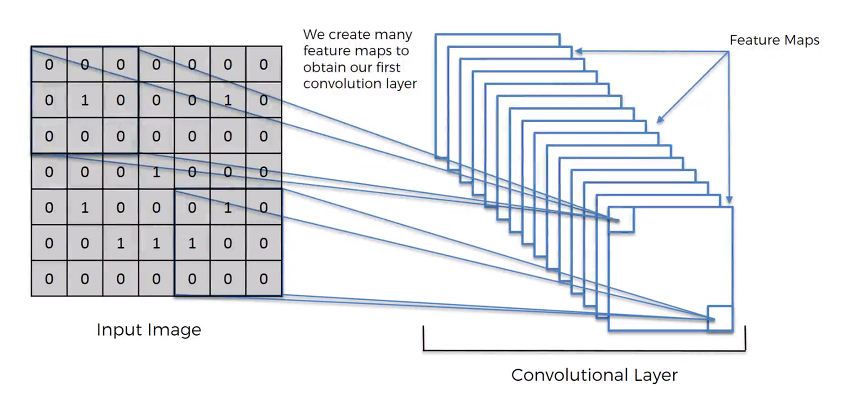
- 이렇게 뽑아낸 Feature Map 들을 잘 살펴보면 얻어낸 Feature 중에서도 가장 중요한 Feature 를 뽑아낼 수 있을 것이고, 이를 위해서 학습하는 역할을 CNN 중 Convolutional Layer 에서 수행합니다.

- 간단히 요약하면, 기존에 나와있던 Convolution 연산을 활용해서 입력 이미지의 특징을 찾는 과정을 수행하는 것이 CNN 내에서 Convolution Layer가 수행하는 역할입니다.
- 이를 GNN 에도 적용해보고자 했습니다.
Spatial Convolutional Network
-
Spatial graph convolution 은 convolution 연산을 graph 위에서 직접 수행하는 방식으로, 각 노드와 가깝게 연결된 이웃 노드들에 한해서 convolution 연산을 수행합니다.
- 즉, 노드와 이웃 노드들을 특정 grid form 으로 재배열하여 convolution 연산을 수행하는 것입니다.
-
그러나 우리가 일반적으로 아는 CNN 의 filter 는 고정된 사이즈를 가집니다.
-
따라서, spatial graph convolution 방식의 관건은 고정된 크기의 이웃 노드를 선택하는 것입니다. 뿐만 아니라, CNN의 특징 중 하나는 “local invariance” 입니다.
- 이는 입력의 위치가 바뀌어도 출력은 동일함을 의미합니다.
-
마찬가지로, Spatial graph convolution의 또다른 관건은 바로 “local invariance”를 유지를 해야한다는 것입니다.
-
앞에서 언급한 spatial graph convolution 이 다뤄야 할 문제점과 별개로 또다른 문제점이 존재합니다. Spatial graph convolution 은 고정된 이웃 노드에서만 정보를 받아서 노드의 정보를 업데이트를 한다는 점입니다.
-
그러나, 그래프에서의 한 노드의 정보는 시간에 따라 여러 노드들의 정보의 혼합으로 표현될 수 있습니다.
- 즉, 고정된 이웃 노드 말고도 멀리 연결되어 있는 노드의 정보도 시간이 흐르면서 밀려 들어올 수 있는 것입니다. 이를 노드 간 message passing이라 합니다.
-
즉, 한 노드의 정보는 여러 노드의 signal 이 혼재해 있는 것으로, 이를 time domain 이 아닌 frequency 도메인으로 분석한다면, 한 노드 내에 혼재된 signal 들을 여러 signal 의 요소로 나눠서 node의 특징을 더 잘 추출할 수 있습니다.
- 이것에 관한 것이 바로 “Spectral Graph Convolution”입니다.
- 이는 spectral 영역에서 convolution을 수행하는 것입니다.
Spectral Convolutional Network
- Signal Processing 분야에서 “spectral analysis” 라는 것은 이미지/음성/그래프 신호(signal)을 time/spatial domain 이 아니라 frequency domain 으로 바꿔서 분석을 진행하는 것입니다.
- 즉, 어떤 특정 신호를 단순한 요소의 합으로 분해하는 것을 의미합니다. 대표적으로 이를 수행할 수 있는 방법이 푸리에 변환(Fourier Transform)입니다.
- spectral analysis에서 입력 신호가 전파/음성신호면 time domain을 frequency domain으로 변환하고, 컴퓨터 비전/그래프/영상처리 분야이면 spatial domain을 frequency domain으로 변환합니다.
- 즉, 어떤 특정 신호를 단순한 요소의 합으로 분해하는 것을 의미합니다. 대표적으로 이를 수행할 수 있는 방법이 푸리에 변환(Fourier Transform)입니다.
Fourier Transform
- 푸리에 변환이란, 임의의 입력 신호를 다양한 주파수를 갖는 주기 함수들의 합으로 분해하여 표현하는 것입니다. 아래 그림처럼 빨간색 신호를 파란색의 주기 함수들의 성분으로 나누는 작업이 바로 푸리에 변환입니다.
- 즉, 파란색 주기함수들을 합하면 결국 빨간색 신호가 되는 것입니다.

- 먼저, 푸리에 변환 식에 대해서 살펴보겠습니다.
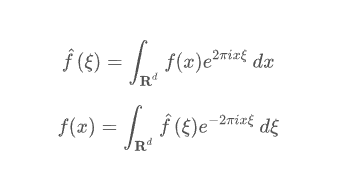
-
위 식은 f 의 푸리에 변환이고, 아래 식은 푸리에 역변환입니다.
- 푸리에 변환은 time domain 을 frequency domain 으로, 푸리에 역변환은 frequency domain 의 함수를 다시 time domain 으로 변환합니다.
-
푸리에 변환을 바라보는 관점 중 하나는 '내적'입니다.
- '내적'은 유사도라는 의미를 내포하고 있습니다. 따라서 푸리에 변환을 다음과 같이 풀어쓸 수 있습니다.
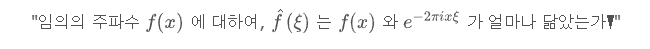
- 그렇다면, e^(-2πixξ) 의 의미를 알아보겠습니다. 이를 오일러 공식으로 표현하면 다음과 같습니다.
- 오일러 공식은 복소지수함수(complext exponential function)를 삼각함수(trigonometric function)로 표현하는 유명한 식입니다.
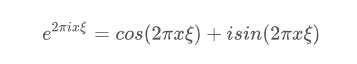
-
즉, 주어진 주파수 f(x) 에 대해 cosine 에서 유사한 정도와 sine 에서 유사한 정도의 합이 푸리에 변환이라고 생각할 수 있습니다.
-
이번엔 푸리에 변환의 선형 대수적인 의미를 살펴봅시다. 선형 대수에서, d 차원에 속한 벡터 a 에 대한 d 차원의 orthonormal basis 를 찾을 수 있다면, 벡터 a 를 orhonormal basis의 선형결합으로 표현할 수 있습니다.
- 이 orthonormal basis 를 찾는 방법 중 하나가 바로 Eigen-value decomposition 입니다.
- orthonormal 이란 서로 직교하면서 길이가 1인 벡터들을 의미합니다. 또한, 모든 matrix에 대해서 eigen-value decomposition 결과로 찾은 basis 가 orthonormal 은 아닙니다. 하지만 real-symmetric matrix 에 대하여 구한 eigenvector 들은 orthgonal한 관계입니다.
- 이 orthonormal basis 를 찾는 방법 중 하나가 바로 Eigen-value decomposition 입니다.
-
참고로, sine 과 sine, sine 과 cosine, cosine 과 cosine을 내적하면 모두 다 0이 나옵니다.
- 즉, 삼각함수는 직교함을 알 수 있습니다.
-
그렇다면 선형대수 관점에서, sine 과 cosine 기저들의 선형 결합이 푸리에 변환이 되는 것입니다.
- 즉, 어떤 특정 graph signal 에 관한 행렬이 존재하고 이 행렬이 real-symmetric matrix 이며 이들의 eigenvectors 를 구할 수 있다면, eigenvector 의 선형 결합이 graph signal 의 푸리에 변환임을 의미하는 것입니다.
Laplacian
-
Graph laplacian 을 보기 전에 Laplace Operator 에 대해 살펴보도록 하겠습니다.
- Laplace operator 는 differential operator 로, 벡터 기울기의 발산(Divergence)을 의미합니다.
-
Divergence가 나타내는 의미, 즉, Laplace operator가 나타내는 의미는 함수의 높고 낮음입니다.
- 이는 이계 도함수의 성질과 비슷합니다. 도함수의 미분 값이 양수면 아래로 볼록이고, 도함수의 미분 값이 음수면 위로 볼록인 것과 유사합니다.
-
그렇다면, graph signal 영역에서 Laplace operator 가 갖는 의미가 무엇일까요?
- graph signal 영역에서 Laplace operator 를 적용한다는 것은, 한 노드에서의 signal 의 흩어짐 정도, 다시 말해 흐르는 정도를 알고자 하는 것입니다. 특정 노드에서 signal 이 들어왔을 때 그 signal 이 특정 노드와 연결된 노드들로 각각 얼마만큼 빠르게 흩어지는지를 알 수 있고 이는 즉 그 노드의 특징이 될 수 있는 것입니다.
-
쉽게 말해, 한 노드의 특징은 해당 노드와 연결된 이웃 노드와의 관계라는 관점에서 표현될 수 있고, 이 표현을 위해 이웃 노드와의 차이를 이용한 것이 laplacian operator 입니다.
Laplacian matrix
-
Laplacian matrix 란 graph representation 중에서 이웃 노드와의 변화 흐름을 통해 노드의 특징을 나타내는 그래프 표현이라고 생각할 수 있습니다.
-
이웃 노드와의 차이(variation)는 결국 노드 간의 매끄러움 정도(smoothness)를 의미합니다.
- 한 노드가 이웃 노드와의 차이가 작다는 것은 그 노드는 이웃 노드와 특성이 비슷한 경우이고, 이를 ‘매끄럽다’라고 생각할 수 있습니다. 면에, 이웃 노드와의 차이가 크다는 건 그 노드는 이웃 노드와 특성이 상이하다는 것이고 이는 ‘매끄럽지 않다’라고 생각할 수 있습니다.
- Laplacian Matrix 는 graph 의 smoothness 와 관련이 있습니다.
-
이를 ‘신호’라는 관점에서 다시 생각해봅시다. 어떤 한 노드 내에서 흐르는 신호를 크게 2가지로 나눈다면, 나와 비슷한 특성을 가진 이웃 노드에서 들어오는 신호와 나와 상이한 특성을 가진 이웃 노드에서 들어오는 신호로 나눌 수 있습니다.
- 즉, 한 노드 내에 혼잡해 있는 신호는 나와 유사한 특성을 가진 노드에서 오는 신호와 나와 상이한 특성을 가진 노드에서 오는 신호의 결합으로 생각할 수 있습니다.
-
이는 결국 푸리에 변환과 관련된 개념입니다. 그리고 나와 유사한 속성의 노드와 상이한 속성의 노드를 나눌 수 있는 것에 관한 정보가 바로 Laplacian matrix 에 담겨져 있는 것입니다. 따라서, lapalcian matrix 를 이용한 푸리에 변환이 바로 “Graph Fourier Transform” 이며, 이는 앞서 언급한 “eigen-value decomposition” 과 관련이 있는 것입니다.
-
Laplacian Matrix 앞서 설명한 Degree Matrix 와 Adjacency Matrix 의 차로 표현됩니다.
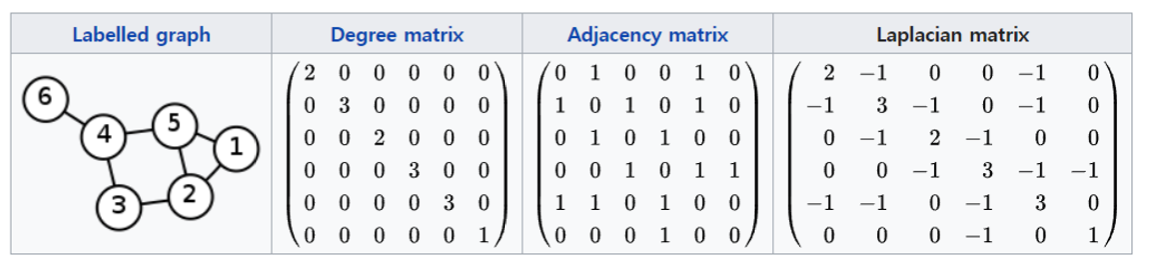
Graph Fourier Transform
-
그렇다면, graph fourier transform 이 왜 Laplacian matrix 를 eigen - decomposition 을 할까요?
-
다음 식은 노드 간의 차이의 합에 관한 식입니다.
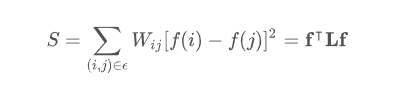
-
이는 결국 graph 의 smoothness 와 관련된 것이며, Laplacian quadratic form 으로 표현이 가능합니다. 위의 식을 최소화하게 하는 f 를 찾는다면, 특정 노드와 특성이 유사한 노드 집단과 상이한 노드 집단을 구분할 수 있습니다.
-
Lagrange 방정식에 의해 최적화 방정식으로 바꾸면 다음과 같습니다.
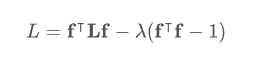
- 위 식을 미분하여 최소가 되게 하는 f 를 찾으면 다음과 같습니다.

-
위의 식은 laplacian 행렬의 eigen-value decomposition 입니다. laplacian matrix 의 eigenvector eigen vector 들이 특정 노드와 유사한 노드 집단과 상이한 노드집단을 구분하는 기준이 되고, 특히 작은 값의 eigenvalue 의 대응하는 eigenvector 일수록 graph 를 더욱 smooth 하게 나누는 기준이 됩니다.
-
이를 fourier transform 관점에서 해석해 봅시다.
-
graph의 특정 노드 signal을 노드의 작은 값의 eigenvalue 에 대응되는 eigenvector 에 사영시키면, 혼재되어 있는 signal 중 가까운 이웃 노드에서 들어오는 signal 의 성분을 추출한 것으로 볼 수 있고, 큰 값의 eigenvalue 에 대응되는 eigenvector에 사영시키면, 혼재되어 있는 signal 중 멀리 있는 상이한 노드에서 들어오는 signal의 성분을 추출한 것입니다.
- 따라서, 혼재되어 있는 graph signal 을 eigenvector의 선형 결합으로 표현하여, 여러 집단에서 들어오는 signal 의 합으로 표현할 수 있습니다.
-
또한 위에서, fourier transform 은 혼합 signal 을 sine 과 cosine 의 주파수의 성분으로 쪼갠 성분들의 선형 결합이라고 하였습니다. 그리고, 이 때 주파수의 성분은 삼각 함수의 직교성으로 인해, 직교 기저를 이룬다고 하였습니다.
- 마찬가지로, laplacian matrix 은 real-symmetric 행렬이어서 eigenvector 들이 직교 기저를 이룹니다.
- 즉, graph signal 을 laplacian eigenvector 행렬에 사영시키면, graph signal을 laplacian의 직교 기저들의 성분으로 분해하여 이를 합한 선형결합에 해당됩니다.
-
따라서 Graph Fourier Transform 은 Laplacian 행렬의 Eigen-value decomposition 과 관련이 있게 되는 것입니다.
-
마지막으로, Graph Fourier Transform의 수식을 정리해보도록 하겠습니다.
-
Laplacian 행렬의 eigen-value decomposition은 아래와 같습니다.
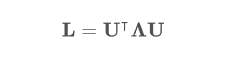
- 이를 이용한 graph fourier transform과 inverse graph fourier transform은 아래와 같습니다.
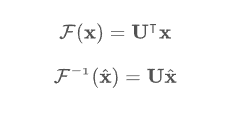
- 아래는 inverse fourier transform 인데, 이는 frequency domain 으로 변환된 signal 을 다시 time domain 으로 변환하는 것입니다.
다시, Spectral Convolutional Network
-
graph convolution 은 어떤 graph의 특징을 추출해 낼 수 있는 filter 를 학습으로 얻고자 하는 것입니다.
-
convolution theorem 의 핵심은 time 영역에서의 signal 과 시스템 함수와의 convolution 연산은 각각 frequency 영역으로 변환한 뒤의 곱과 같다는 것이었습니다.
- frequency 영역에서의 convolution 은 단순 곱으로 계산될 수 있기 때문에 훨씬 편리합니다.
-
마찬가지로 graph 영역에서도 graph signal 을 fourier transform 으로 frequency 도메인으로 바꿔서 계산하면 편리합니다. 또한 노드와 가까이 있는 이웃 노드에서부터 멀리 떨어져 있는 노드에서 오는 신호까지 모두 고려하여 graph signal 의 특징을 추출할 수 있게 되는 것입니다.
- 이것이 바로 ‘Spectral Graph Convolution’ 입니다.
-
Spectral Graph Convolution 식은 아래와 같습니다.
- 이 식에서 학습할 filter는 g 입니다.
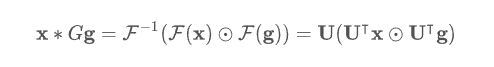
- 이 식을 다음과 같이 가정(학습할 filter가 대각요소만 있다고 가정)하면,
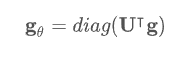
- 다음과 같은 식이 됩니다.
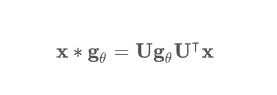
Graph Pooling
-
그러나 Spatial Convolutional Network 와 Spectral Convolutional Network 모두 Scalability issue 가 존재했습니다.
- 이를 방지하기 위해, Graph Pooling 을 도입하였습니다.
-
Pooling 은 CNN 에서 계산의 효율성을 높이기 위해 사용하였는데, 이를 Graph 에도 사용해보고자 한 것입니다.
- Pooling 을 하는 가장 큰 이유는 입력 데이터의 차원 감소입니다. 또한, 오버피팅을 방지하는 효과도 있습니다.
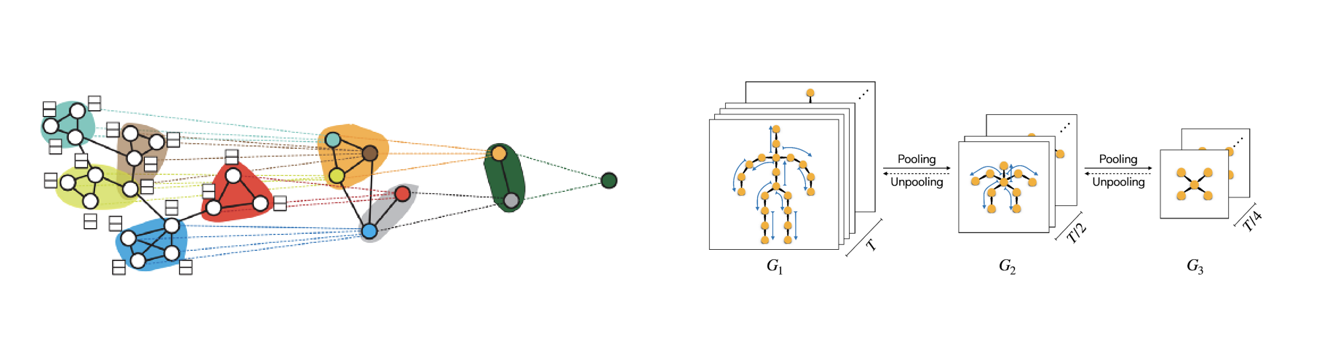
Variational Graph Auto Encoder
Auto Encoder
-
Auto Encoder 는 딥러닝에서 가장 대표적인 unsupervised learning 방식 중 하나입니다.
-
Auto Encoder 에 대해서는 다음 링크를 참고해주시면 감사하겠습니다.
다시, Variational Graph Auto Encoder
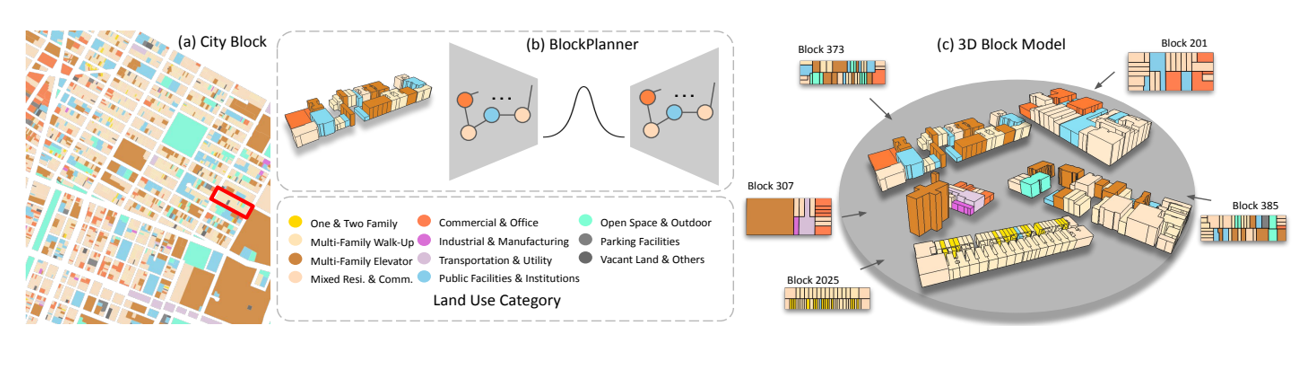
- Input 을 Graph 의 형태로 입력 받아 실행하려는 시도가 바로 GAE 입니다.
- GAE 에서는 주로 VAE 를 사용합니다.
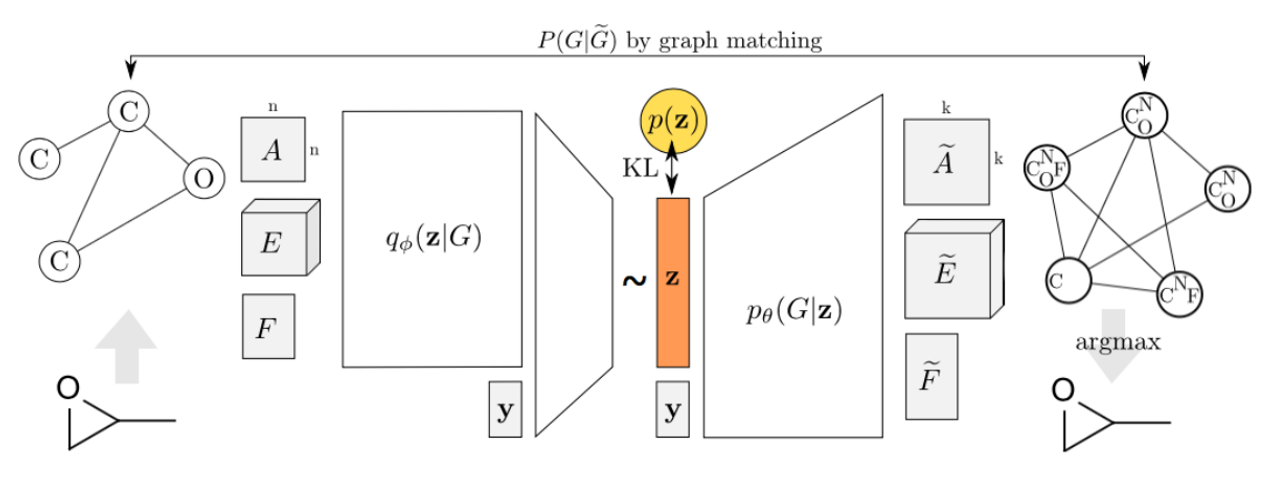
- 활용 분야로는 Block Planner 가 있습니다.
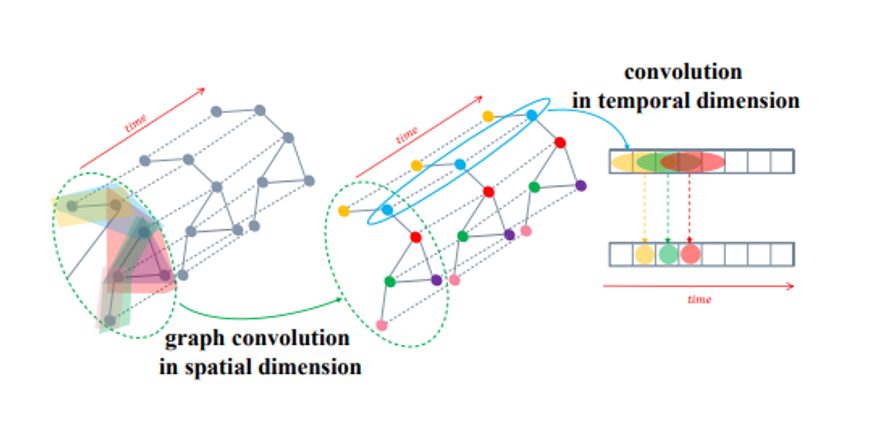
Spatial - Temporal Graph Neural Network
-
Spatial Convolution 과 Temporal Convolution 을 결합한 GNN 입니다.
- 시간에 따라 feature 가 달라지는 Graph 를 활용할 때 이점을 가집니다.
-
활용 분야로는 Motion puzzle 이 있습니다.