앞서 글에 올린 큐(queue)는 First In, First Out(FIFO) 방식으로 항목을 처리하는 리스트였다. 근본적으로 큐 끝에서만 데이터를 삽입하고 큐 앞에서만 접근과 삭제를 수행한다.
우선순위 큐(priority queue)
우선순위 큐(priority queue)는 삭제와 접근에 있어 큐와 흡사하나 삽입에 있어 정렬된 배열과 비슷한 리스트다. 즉 우선순위 큐 앞에서만 데이터에 접근하고 삭제하되 데이터를 삽입할 때는 데이터를 늘 특정 순서대로 정렬시킨다.
우선순위 큐를 간단하게 구현하려면 정렬된 배열을 이용하면 된다. 즉, 배열을 사용하되 다음의 조건이 있다.
- 데이터를 삽입할 때 항상 적절한 순서를 유지
- 데이터는 배열 끝에서만 삭제한다. ( 배열 끝이 우선순위 큐의 앞이다. )
효율성을 분석해보자.
우선순위 큐의 주요 연산은 삭제와 삽입이다.
일반적인 배열에서 삭제는 인덱스0에 생긴 빈 자리를 메우기 위해서 모든 데이터를 시프트해야 하므로 시간복잡도는 O(N)이다. 하지만 배열 끝을 우선 순위 큐 앞으로 삼으면 항상 배열 끝에서 삭제하기 때문에 시간 복잡도는 O(1)이다.
하지만 삽입은 데이터를 넣을 자리를 알아내기 위해 배열 원소 N개를 모두 확인해야 하기 때문에 기존 배열과 마찬가지로 O(N) 이다. 항목이 많아지면 원치 않은 지연이 발생 할 수 있다. 그래서 우선순위 큐보다 효율적인 또 다른 자료 구조를 찾아낸 게 바로 힙이다.
힙(heap)
이진 힙(binary heap)
이진 힙은 특수한 종류의 이진 트리다.
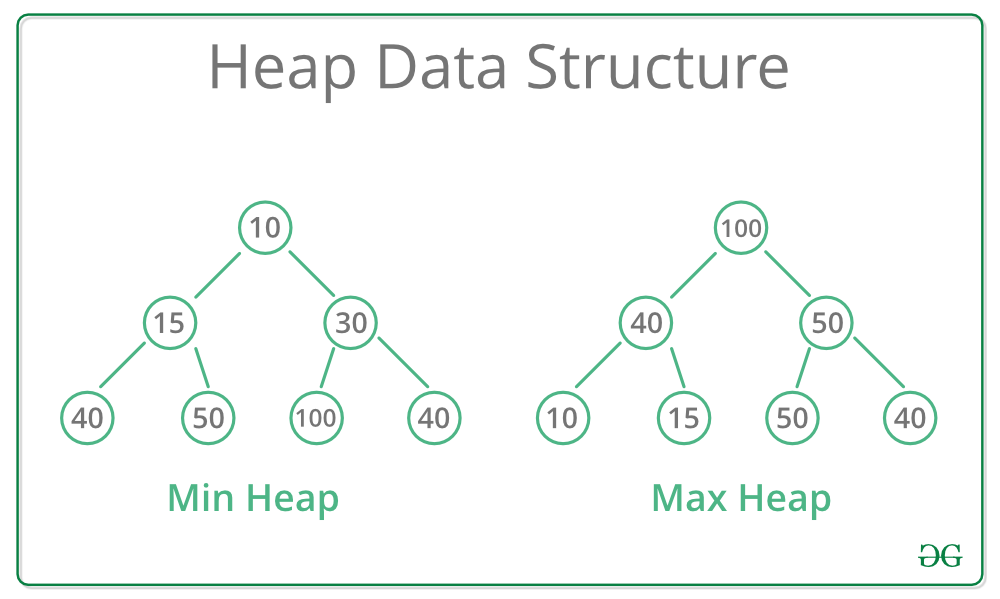
이진 힙에도 최대 힙(max-heap)과 최소 힙(min-heap)이라는 두 종류가 있다.
힙은 다음의 조건을 따르는 이진 트리다.
- 각 노드의 값은 그 노드의 모든 자손 노드의 값보다 커야 한다. 이 규칙을 힙 조건(heap condition)이라 부른다.
- 트리는 완전(complete)해야 한다.(완전 이진 트리 형태)
힙 조건
힙 조건(heap condition)이란 각 노드의 값이 그 노드의 모든 자손보다 커야 한다는 뜻이다.
사진을 보면 각 노드의 값이 모든 자손 노드보다 크므로 다음 트리는 힙 조건을 만족한다.
사진은 최대 힙을 예로 들었지만 힙의 루트노드에는 항상 데이터들 중 가장 큰 값(혹은 가장 작은 값)이 저장되어 있기 때문에, 최댓값(혹은 최솟값)을 O(1)O(1)안에 찾을 수 있다.
트리가 완전해야 한다는 두번째 힙 규칙을 살펴보자.
완전 트리(complete tree)는 빠진 노드 없이 노드가 완전히 채워진 트리다. 따라서 트리의 각 레벨을 왼쪽부터 오른쪽으로 읽었을 때 모든 자리마다 노드가 있다. 하지만 바닥 줄에는 빈 자리가 있을 수 있다. 단 빈 자리의 오른쪽으로 어떤 노드도 없어야 한다.
위의 트리는 바닥 줄에 빈 자리가 없고 부모노드와 자식노드의 대소관계도 정확하므로 힙 조건을 만족하는 완전한 트리라고 할 수 있다.
최대힙을 기준으로 힙의 속성에 대해 몇가지를 들겠다.
- 힙에서는 루트 노드가 항상 최댓값이다.(최소 힙에서는 항상 최솟값)
- 힙에는 마지막 노드(last node)가 있다. 힙의 마지막 노드는 바닥 레벨에서 가장 오른쪽에 있는 노드다.(위 최대힙에서는 40이다)