이전 포스팅에서는 Shannon's source coding theoren에 관한 수학적 내용을 정리했다. 이번에는 그를 응용하여 데이터를 압축하는 symbol codes에 대해 알아보자.

Source Coding Theorem for Symbol Codes

이번에는 ensemble X를 encoded symbol 로 만들어보고자 한다. 이때 code C 의 길이는 variable할 수 있다고 하면, 주어진 X에 대해 “평균”적인 code 길이는 $L(C, X)$라 하고, 아래 부등식을 만족한다.

즉, encoded symbol 의 평균 길이가 H(X)와 H(X)+1 사이라는 것. 이때 평균 길이가 H(X)보다 작으면 정보를 제대로 저장할 수 없다고 판단한다. $H(X) = L(C, X)$ 등호는 각각의 outcome에 대한 code 길이가 Shannon information content 와 동일할 때 성립한다.

📌 등호 성립 조건이 그러한 이유는?

생각을 해보면 H(X), X에 대한 엔트로피는 Shannon information content 의 평균값이다. 따라서 $L(C, X)$에서 C의 길이가 Shannon information content인 $\log _2 {1\over P(X)}$를 만족한다면 결국 $H(X)=L(C,X)$가 된다.

Symbol Codes

우선 binary symbol codes 를 보자. binary symbol code C는 아래처럼 정의된다.

이때 $\{0, 1 \}^+$는 집합 원소로 만들 수 있는 유한한 길이의 모든 string 집합이다.

따라서 binary symbol code는 알파벳으로 부터 코드 집합으로 매핑하는 함수라 볼 수 있다. $c(x)$는 $x$에 대응하는 codeword 를 뜻하며, $l(x)$는 그 codeword의 길이를 나타낸다.

이때 code C를 확장한 것을 $C^+$로 표기하며 이는 단순히 각각의 codeword를 concatenate한 것과 같다.

아래 예시를 보면 확실히 이해할 수 있을 것이다.

Prefix Codes

Prefix를 알기 전에 uniquely decodable code 에 대해 먼저 정리하고 가자. uniquely decodable code는 말 그대로 서로 다른 두 string은 서로 다른 인코딩을 가진다는 말이다. 즉 string이 다르면 인코딩도 다르다는 말. 수식으로 보면 다음과 같다.

그럼 prefix 는 뭘까?

한 단어 c 가 다른 단어 d 의 prefix 라 하고 d에서 c부분을 잘라내고 남은 부분을 tail t 라고 하자. 그럼 자연스레 ct = d가 된다. 이를 만족하는 c를 prefix라고 한다.

예를 들어 d = 101이라면 c = 1(t=01) 또는 c = 10(t=1)이 될 수 있다.

한 걸음 더 나아가 이번에는 prefix codes 의 정의로 가보자.

이제 prefix가 무엇인지 알았으므로 prefix codes는 사실 쉽다. code의 prefix, 즉 겹치는 부분이라 생각해면 된다. 하지만 prefix codes의 정의는 그러한 겹치는 부분이 없는 코드라고 생각하면 된다.

특정 codeword가 다른 codeword의 prefix가 아닐 경우에 이 코드를 prefix code 라 부른다는 것이다. (왜 이름을 이렇게 지었는지 모르겠다.. 적어도 Non prefix-code 라고 지어야하는거 아닌감😢 )

결국 codewords들 사이에 겹치는 표현이 없는 Code를 prefix code라 한다. 예시를 보면 이해하기 쉬울 것이다.

Example

$C_1 = \{0, 101 \}$: $C_1$은 prefix codes 다. 모든 codeword에 대해 서로 prefix가 될 수 없으므로! 다시 말해 codeword 101에서 가능한 prefix는 1 , 10 이 있지만 그러한 codeword가 존재하지 않는다.

$C_2 = \{1, 101 \}$: $C_2$는 prefix codes 가 아니다. 위의 예시를 봤으니 당연한 소리. 1 은 101 의 prefix이다.

$C_3 = \{0, 10, 110, 111 \}$: $C_3$은 prefix codes 다. 서로 prefix가 될 수 없으므로!

여기서 하나 얻을 수 있는 인사이트는 prefix codes를 binary tree 로 나타낼 수 있다는 점! Binary tree를 그린다면 complete prefix codes는 모든 가지의 leaves를 나타낸다.

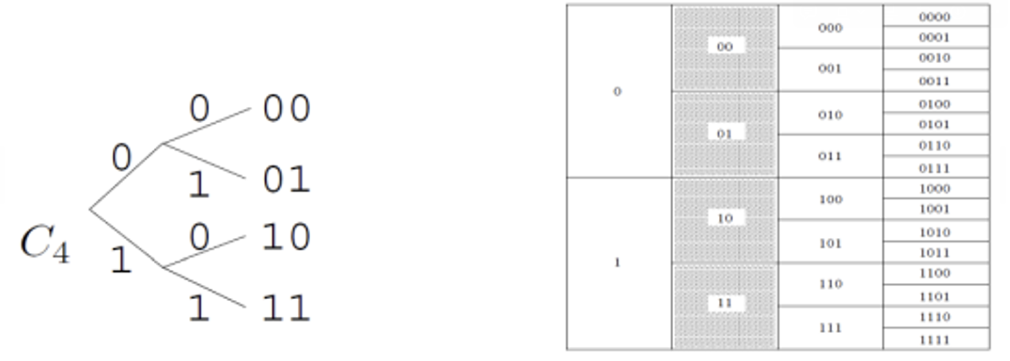
따라서 $C_4 = \{00, 01, 10, 11 \}$을 complete prefix codes 라 부른다.

그럼 다시 코드의 길이로 넘어오자.

앞에서 r.v. X에 대해 평균 코드 길이를 $L(X, C)$로 표현한다고 했다. 이를 다시 써보면

Example

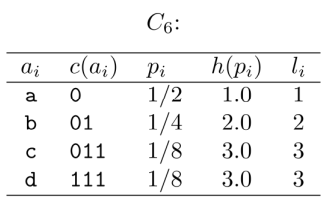
ensemble X가 다음과 같이 정의되어 있을 때 code $C_3$는 다음과 같다.

$C_3$의 column은 각각 알파벳, 코드, 확률, Shannon information contents, 코드 길이를 뜻한다.

이때 H(X) = 1.75bits이며 $L(C, X)$도 동일하게 1.75bits가 된다. 이때 $C_3$은 prefix code 이며 uniquely decodeable 하다.

그럼 이어서 $C_4, C_5$의 경우를 보자.

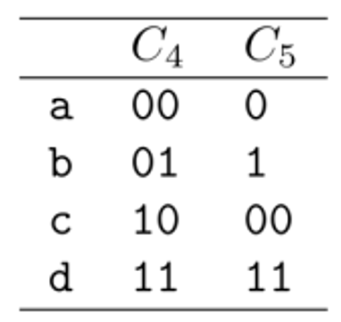
$C_4$의 경우 $L(C_4, X)$ = 2bits이므로 H(X) = 1.75bits보다 크다.

$C_5$의 경우 $L(C_5, X)$ = 1.25bits이므로 H(X)보다 작다. 또한 $C_5$는 not uniquely decodable.

e.g.) $c^+(aabb) = c^+(cd) = 0011$ → Not uniquely decodable

이번에는 $C_6$를 보자.

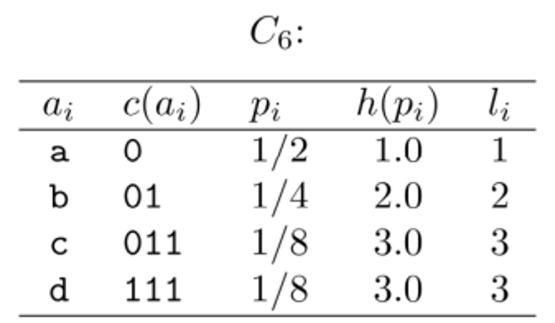
$C_6$의 경우 $L(C_6, X)$ = 1.75bits이므로 H(X)와 동일하다.

• $C_6$은 Not prefix codes 이다.
• $C_6$은 uniquely decodable codes 이다.

📌 Prefix code와 uniquely decodable codes의 관계

한 코드 C가 prefix code라는 것은 codeword끼리 prefix가 되지 않는 다는 말이므로 결국 임베딩이 다를 수 밖에 없다. 하지만 역은 항상 성립하지 않는다. $C_6$의 예시를 봐도 uniquely decodable codes이지만 prefix codes가 아닌 경우를 알 수 있다.

Kraft Inequality

이번에는 이어서 Kraft inequality를 알아보자. Kraft inequality는 codewords 의 길이 집합이 주어졌을 때 이에 대응하는 prefix code 의 존재를 입증하는 부등식이다. 그럼 어떠한 부등식인지 알아보자.

Binary alphabet {0, 1}로 만든 모든 uniquely decodable code C(X)에 대해서, codewords의 길이는 아래 부등식을 무조건 성립한다.

이때 $I=|A_X|$이다. 즉 모든 codeword의 길이 $l_i$에 대해 $1 \over 2^{l_i}$의 합이 1보다 작거나 같다는 의미. 여기선 식에서 볼 수 있듯이 알파벳의 확률 분포와는 무관하게 단지 codeword의 길이에만 상관이 있다.

위키피디아의 내용을 통해 위 부등식이 무엇을 뜻하는지 알아보자.

📝 Kraft's inequality limits the lengths of codewords in a prefix code:
if one takes an exponential of the length of each valid codeword, the resulting set of values must look like a probability mass function, that is, it must have total measure less than or equal to one. Kraft's inequality can be thought of in terms of a constrained budget to be spent on codewords, with shorter codewords being more expensive.

위의 내용을 한글로 정리하면 이렇다.

Kraft inequality는 각각의 codewords의 길이를 2의 지수로 받는다. 이때 결과로 나온 값은 어떻게 보면 probability mass function으로 볼 수도 있다. 따라서 결과값들의 합은 1 이하가 되어야 한다.

이는 결국 Kraft inequality가 “codewords를 만드는데 사용하는 bits 길이 조건”이라 볼 수 있다. 즉, bits 수가 적을 수록 더욱 expensive하다는 의미.

이때 등호는 Complete 할 때 성립한다.

아까 prefix가 결국 binary tree를 그리는 것과 동일하다는 이야기를 잠깐 한 적이 있다. 만일 prefix code C(X)가 binary tree의 모든 leaves의 codewords로 이루어져 있다면 이를 complete prefix code라고 했다.

여기서는 uniquely decodable code 가 등호를 만족할 때 complete code라고 한다.

📌 Kraft inequality와 prefix code의 관계를 보자.

Kraft inequality를 만족하는 codeword lengths의 집합이 주어졌을 때, 이러한 길이를 가지는 uniquely decodable prefix code 가 존재한다.

즉, Kraft inequality를 만족하는 codeword 길이 집합이 있으면, 이에 정확히 대응하는 prefix code를 찾을 수 있다는 말.

Proof of the Kraft inequality

ref: McMillan_inequalityhttps://athena.nitc.ac.in/~kmurali/Courses/ITAug11/kraft.pdf

우선 노테이션부터 정리해보면,

• $\{ l_i\}$: code C의 코드 길이 집합, $i \in [1, I]$ ($I = |A_X|$)
• $l_\text{min}, l_\text{max}$: codeword의 길이 중 최솟값, 최댓값

Kraft inequality의 sum 항을 S로 두고 N제곱을 씌워보자.

code C 의 N개의 codewords의 길이를 $l = l_{i_1}+...+l_{i_N}$로 나타낸다. 즉, 코드 C 안에 $|A_X|=N$개 만큼의 codewords가 있고, $S^N$에서는 N개의 codewords를 선택하여 나타낸 시퀀스다.

이때 $A_l$은 총 길이가 $\mathbf{l}$인 codewords들의 가능한 개수라고 하자. 다 합쳐서 총 길이가 $\mathbf{l}$이 되게끔 하는 n개의 codewords 경우의 수라고 보면 된다.

그럼 $A_l$의 최소는 N개의 string이 모두 최소 길이를 가질 때이므로 $Nl_\text{min}$이 된다. 반대로 $A_l$의 최대는 N개의 string이 모두 최대 길이를 가질 때이므로 $Nl_\text{max}$가 된다.

이를 이용하여 $S$를 $A_l$에 대해 다시 쓸 수 있다.

이때 잘 생각해보면 길이가 $l$인 가능한 바이너리 시퀀스는 총 $2^l$이 될 것이다. 그렇자면 C는 uniquely decodable 하기 때문에 만들 수 있는 길이 $l$짜리 시퀀스는 $2^l$보다 작을 수 밖에 없다.

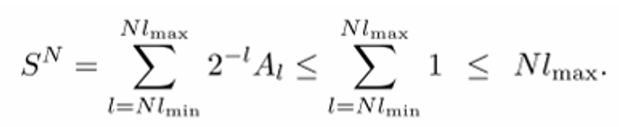
따라서 $S^N \le Nl_\text{max}$가 성립한다. 이때 만약 $S>1$이라면 좌항은 기하급수적으로 증가하는 반면에 우항은 linear하게 증가한다. 따라서 부등식이 성립하기 위해서 $S \le 1$을 만족해야 한다.

내용이 많아 정리하다 보니 포스팅이 길어졌다. source coding theorem과 그를 이용한 symbol code에 대해 자세히 다뤘다. 다음 포스팅에서는 Channel에 대해서 정리해보도록 하겠다 ✅