이전 포스팅에서는 데이터 압축에 관한 내용을 정리했다. 이번에는 이어서 가장 중요한 이론 중 하나인 shannon의 source coding theorem을 정리해보고자 한다.

Shannon’s Source Coding Theorem

엔트로피가 너무 많아서 헷갈리기 시작하니 잠시 용어정리 좀 하고 가자.

• $H(X)$: entropy , r.v. X의 엔트로피, Shannon’s information centent의 평균값
• $H_0(X)$: raw bit contents , 정보 압축 없이 r.v. X의 정보량을 나타내는 값
• $H_\delta (X)$: essential bit contents , 확률 값이 큰 데이터만 선별한 후의 정보량

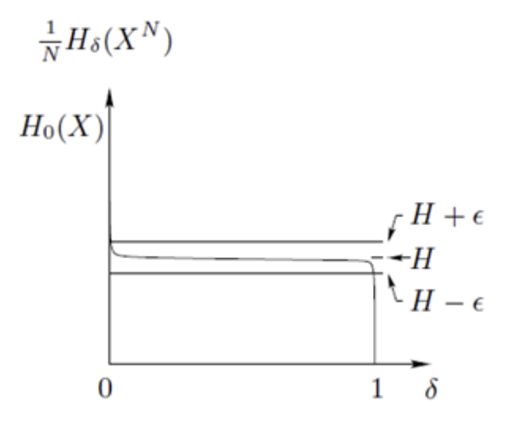
그럼 이제 이 세 엔트로피 사이의 관계를 살펴보자.

우선 앞서 말했듯, $H_0(X)$는 결국 $\delta =0$인 $H_\delta(X)$의 특별 케이스이다. 따라서 위의 그림을 보면 $\delta = 0$인 지점이 $H_0(X)$인 것을 볼 수 있다.

그래프는 ${1\over N} H_\delta (X^N)$를 나타낸 것이다. 이때 N이 무한대로 한다면 그래프가 y=H인 직선과 매우 가까이 다가간 다는 것을 볼 수 있다. 이때 H 는 $H(X) = H \text{bits}$이다. 즉, N이 매우 클 때 essential bit contents 를 normalize 시켜주면 결국 H(X) 와 같음을 알 수 있다.

📌 그래서 이게 무슨 의미인데?

$X^N$, 즉 동일한 확률 분포에서 i.i.d. 로 추출된 N 길이의 시퀀스가 있을 때, 이를 loss를 최소화하여 압축하는 데에 필요한 bits는 결국 NH(X)와 동일하다는 말이 된다. 따라서 N 이 충분히 클 때, 길이 N 의 시퀀스를 표현하는 데에 필요한 bits는 결국 하나의 결과값(symbol)의 엔트로피 H(X)를 N번 구하는 것과 같다!

Typical set

이번에는 효율적으로 데이터를 압축하기 위해서 어떤 데이터를 선택해야 하는지 알아보자. Typical set은 이름 그대로 “Typical”한 집합, 즉 “일반적”이고 “예상되는” 집합이라는 의미다. r.v. X가 있을 때 typical set은 주어진 확률 분포에서 높은 확률을 가지는 길이 N 짜리 시퀀스로 이루어진 집합니다.

더 디테일하게 설명해보면 이렇다.

r.v. X 가 있고, 이에 대해 i.i.d. 로 샘플링된 길이 N짜리의 시퀀스 $x_1, x_2, x_3, ..., x_N$이 있다고 하자. 여기서 Typical set 는 아래 조건을 만족하는 시퀀스들을 집합이다.

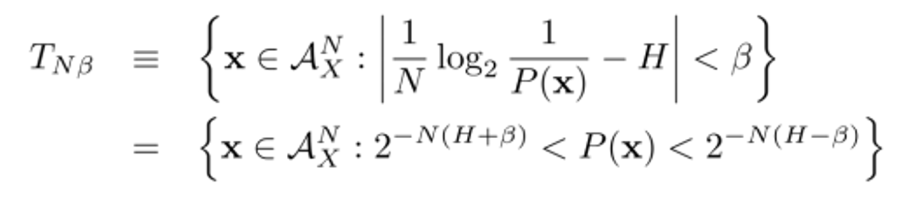
$p(x_1, x_2,..., x_N)$의 확률이 위 부등식 조건을 만족하는 모든 시퀀스를 포함하는 집합이라 보면 된다.

Example

예시를 들어보자. $A_X = \{ a_1, a_2, ..., a_I \}$이고, X는 $a_i$의 개수가 $Np_i$로 정해진 시퀀스라고 하자.

📌 쉽게 말해 $A_X=\{0, 1\}, P_X = \{{1 \over 3}, {2 \over 3} \}$라고 하자.

총 길이가 6인 시퀀스를 만든다고 할 때, 0이 등장하는 개수는 $6 \times {1 \over 3} = 2$, 1이 등장하는 개수는 $6 \times {2 \over 3} = 4$가 된다. 따라서 $a_i$가 시퀀스에 등장하는 개수는 $Np_i$라 정리할 수 있다.*

그럼 시퀀스의 확률 분포는 다음과 같다.

방금 예시에서는 $p(\mathbf{x}) = \{{1 \over{3}}^2, {2 \over 3} ^4 \}$가 되는 셈이다.

그럼 이 확률 분포에 log를 씌워보면 어떻게 되는지 보자.

결과로 NH가 나왔다. 이는 즉 $\mathbf{x}$가 이미 typical set 임을 뜻한다.

Asymptotic Equipartition Property(AEP)

i.i.d. 하게 핸덤 샘플링된 시퀀스 $X^N$가 있을 때, 만일 N이 충분히 크면 $\mathbf{x} \in A^N_X$는 다음 두 프로퍼티를 만족할 확률이 매우 크다.

1. $\mathbf{x}$는 $2^{NH(X)}$개의 원소만을 가지는 $A_X^N$의 부분집합에 속한다

2. 이때 각각이 가지는 확률은 $2^{-NH(X)}$에 ‘근접’하다

이게 도대체 무슨 소리인가. 차근 차근 다시 이해해보자.

우선 r.v. X 를 모두 표현하기 위해 필요한 bits 수는 $H_0(X)$이다. 그럼 길이 N 인 시퀀스를 표현하기 위해 필요한 bits 수는 $H_0(X^N) = NH_0(X)$가 된다. 이때 X는 i.i.d. 하게 샘플링 되었으므로 등식이 성립한다.

여기서 하나만 체크해보자. 길이 N인 시퀀스를 표현하는데 필요한 bits 수가 $NH_0(X)$라는 것은, 표현 가능한 시퀀스의 개수가 $2^{NH_0(X)}$라는 것과 동일하다. (3bits로 표현할 수 있는 데이터의 가지 수는 $2^3 = 8$개)

따라서 길이 N 의 시퀀스가 가지는 전체 집합의 크기는 $2^{NH_0(X)}$이 된다.

그런데 1번 프로퍼티를 보면, N이 충분히 클 때 $\mathbf{x}$는 $A_X^N$의 부분 집합 중 원소를 $2^{NH}$개 가지는 부분집합에 높은 확률로 속해있다고 한다.

쉽게 설명하면 N이 충분히 클 때 데이터는 $2^{NH}$개가 매우 밀접히 모여있다는 뜻. 이때 각각의 데이터가 가지는 확률은 $2^{-NH}$에 근접 하다. 왜일까?

방금 언급한 것 처럼 $\mathbf{x}$는 길이 N 짜리 시퀀스들이며, 매우 높은 확률로 시퀀스는 크기가 $2^{NH}$인 집합에 속한다고 했다. 모든 시퀀스들이 i.i.d 를 따르기 때문에 이 집합 내에 든 시퀀스들의 확률은 $2^{-NH}$에 근접하게 된다.

Inequalities

(1) Markov inequality

Markov inequality 에 따르면 r.v. X와 상수 $\alpha >0$에 대해 아래 부등식이 성립한다.

Proof:

$Y = {|X| \over \alpha}$로 치환했을 때 $P(Y\ge1) \le {E|X| \over \alpha}$를 보이면 된다.

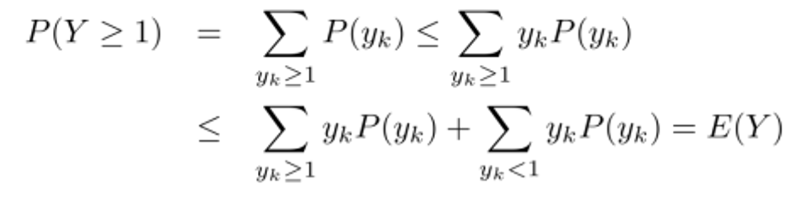
(2) Chebyshev inequality

여기서는 Markov inequality를 응용해서 만들어진 부등식으로, X가 평균 $\mu$, 분산 $\sigma^2$가 있을 때 아래 부등식을 만족한다.

여기까지 Shannon's source coding theorem과 그에 관련된 개념들을 정리해보았다. 다음 포스팅에서는 Symbol codes에 대해서 이어나가 보겠다:)