공부하는 중이라 부정확하고 부족한 지식일 수있습니다! 댓글로 지적 부탁드립니다!

경로(Path)

• R을 집합 A에 관한 관계라고 할때, a부터 시작하여 b에서 끝나는 유한수열
  $π = a, x_1, x_2, ... x_{n-1}, b$ (a에서 b까지의 길이가 n인 경로)

예제1

R = {(1,2),(2,2),(2,3),(2,4),(2,5),(4,3),(5,1),(5,4)}에서 길이가 2인 경로를 찾아라.

• $π_1 = 1,2,3$
• $π_2 = 1,2,2$
• $π_3 = 1,2,4$
• $π_4 = 1,2,5$
• $π_5 = 2,2,2$
• $π_6 = 2,2,3$
• $π_7 = 2,2,4$
• $π_8 = 2,2,5$
• $π_9 = 5,1,2$
• $π_{10} = 5,4,3$

순환(Cycle)

자신에서 시작하여 자신에서 끝나는 경로

관계와 경로

• 길이가 n인 관계 $R^n$
  $xR^ny$는 x에서 시작하여 y로 끝나는 길이가 n인 경로 존재
• 연결관계(Connectivity Relation) $R^∞$
  $xR^∞y$는 x에서 시작하여 y로 끝나는 경로 존재
• 도달관계(Reachability Relation) $R^*$
  x=y 혹은 $xR^∞y$
  유향그래프에서 임의의 두 정점 사이에 도달 관계 성립시, 강하게 연결(Strongly Connected)

예제2

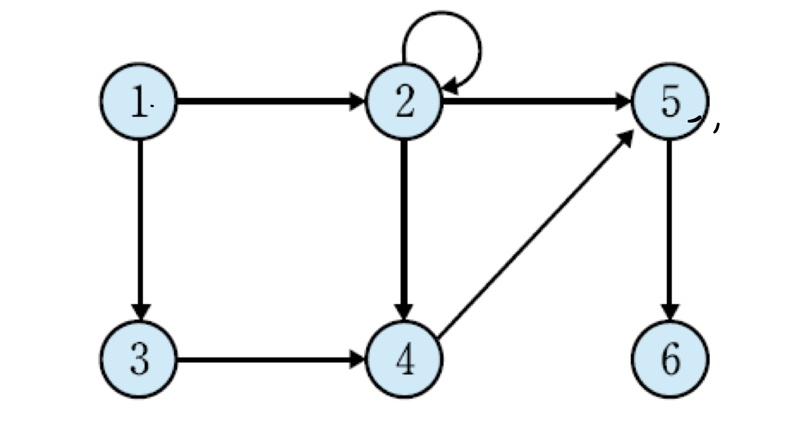
A = {1,2,3,4,5,6}이고 유향그래프가 다음과 같을 때, 관계 R로부터 경로의 길이가 2인 경로들을 모두 찾아라

• $1R^22$ =>1,2,2
• $1R^24$ =>1,2,4
• $1R^25$ =>1,2,5
• $2R^22$ =>2,2,2
• $2R^24$ =>2,2,4
• $2R^25$ =>2,2,5
• $2R^26$ =>2,5,6
• $3R^25$ =>3,4,5
• $4R^26$ =>4,5,6
  
  $R^2$ = {(1,2),(1,4),(1,5),(2,2),(2,4),(2,5),(2,6),(3,5),(4,6)}

A = {a,b,c,d,e}, R = {(a,a),(a,b),(b,c),(c,d),(c,e),(d,e)}일 때, 다음을 구하여라

1. $R^2$

• $aR^2a$ => a,a,a
• $aR^2b$ => a,a,b
• $aR^2c$ => a,b,c
• $bR^2d$ => b,c,d
• $bR^2e$ => b,c,e
• $cR^2e$ => c,d,e
  
  * $R^2$ = {(a,a),(a,b),(a,c),(b,d),(b,e),(c,e)}

2. $R^∞$
   경로의 길이에 상관없이 경로가 있는 모든 순서쌍을 구하면 된다.

• a에서 갈 수 있는 노드 = {a,b,c,d,e}
  {(a,a),(a,b),(a,c),(a,d),(a,e)}
• b에서 갈 수 있는 노드 = {c,e,d}
  {(b,c),(b,e),(b,d)}
• c에서 갈 수 있는 노드 = {e,d}
  {(c,e),(c,d)}
• d에서 갈 수 있는 노드 = {e}
  {(d,e)}
• e에서 갈 수 있는 노드 = ø
  
  
  $R^∞$ = {(a,a),(a,b),(a,c),(a,d),(a,e),(b,c),(b,e),(b,d),(c,e),(c,d),(d,e)}

부울곱을 이용해 길이가 n인 경로 찾기

관계 R의 관계 행렬 $M_R$일때, $M_{R^n}$ = $(M_{R})^n$ = $\underbrace{M_R\odot\ M_R\odot\ M_R\odot ... \odot\\M_R}_{\text{n개}}$

부울곱(Boolean Product)

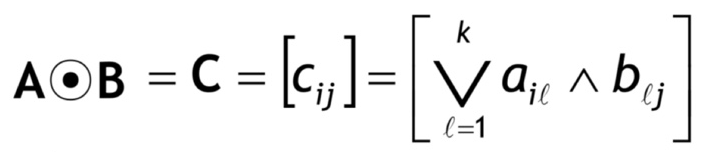
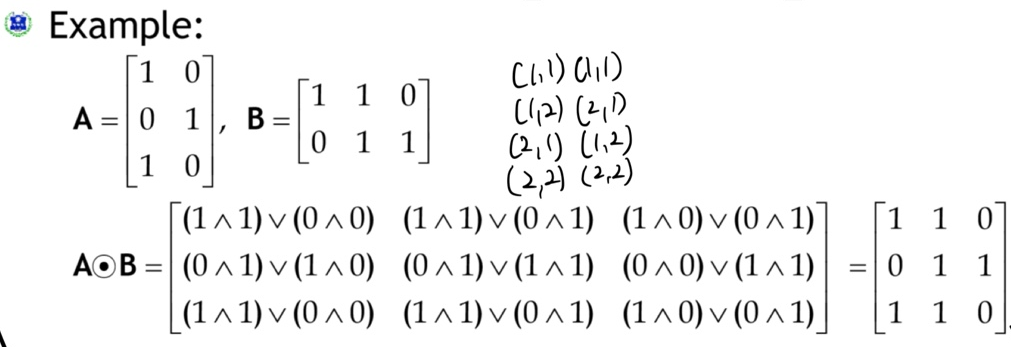
예제3

관계 R = {(a,a),(a,b),(b,c),(c,d),(c,e),(d,e)}일 때, 부울곱을 이용해서 $R^2$을 구하여라.

관계 행렬 $M_R$을 구하면

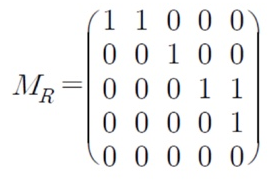
$M_{R^2}$을 부울곱을 통해 구하면

따라서 관계 행렬 $M_{R^2}$을 통해 $R^2$를 구하면

$R^2$ = {(a,a),(a,b),(a,c),(b,d),(b,e),(c,e)}

경로의 합성(Composition of Path)

• $π_1$의 경로 = $a, x_1, x_2, x_3 ... x_{n-1}, b$
• $π_2$의 경로 = $b, y_1, y_2, y_3 ... y_{n-1}, c$
• $π_1$과 $π_2$ 합성 경로 = $π_1·π_2$ = $a, x_1, x_2, x_3 ... x_{n-1}, y_1, y_2, y_3 ... y_{n-1}, c$
• $π_1$과 $π_2$의 합성이 되기 위해서는 $π_1$의 끝나는 정점과 $π_2$의 시작 정점이 같을때만 가능

예제4

두 경로 $π_1$ = 1,2,3과 $π_2$ = 3,5,6,2,4일 때, 합성 $π_1·π_2$를 구하여라.

$π_1$의 끝나는 정점 = 3, $π_2$의 시작 정점 = 3 이므로 합성 가능

$π_1·π_2$ = 1,2,3,5,6,2,4

역경로(Inverse Path)

경로 $π$ = $a, x_1, x_2, x_3 ... x_{n-1}, b$일 때,
역경로 $$π^{-1}$$ = $$b, x_{n-1},... x_3,x_2,x_1, b$$

예제5

두 경로 $π_1$ = 1,2,3과 $π_2$ = 3,5,6,2,4일 때, 역경로를 구하여라.

• $π_1^{-1}$ = 3,2,1
• $π_2^{-1}$ = 4,2,6,5,3