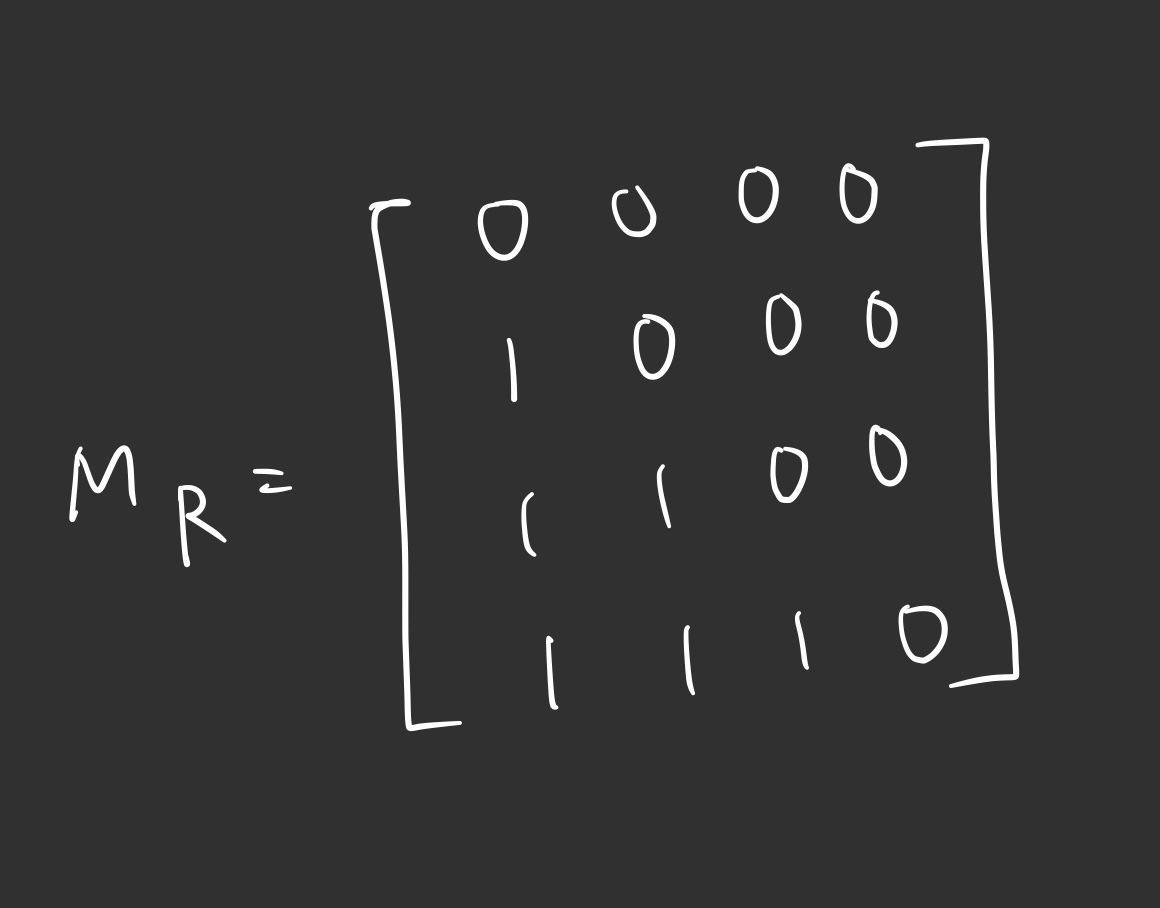공부하는 중이라 부정확하고 부족한 지식일 수있습니다! 댓글로 지적 부탁드립니다!

관계와 관계 표현

---

이항관계(Binary Relation)

• 집합 A,B에 대해 A에서 B로 가는 관계
• 이항관계 R은 AxB의 부분집합
• x ∊ A와 x ∊ B에 대해 순서쌍 (x,y) ∊ R이면 x는 y에 대해 R의 관계에 있다고 하며 xRy로 표기

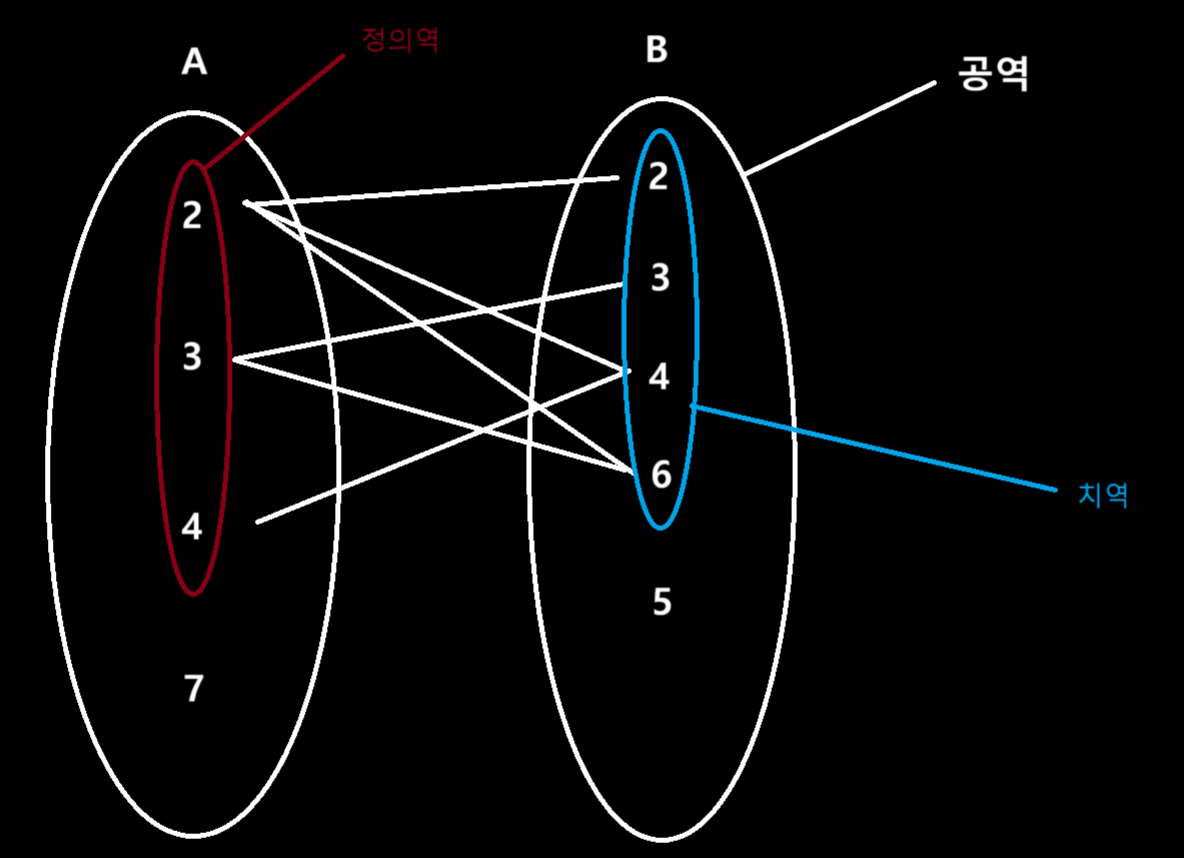
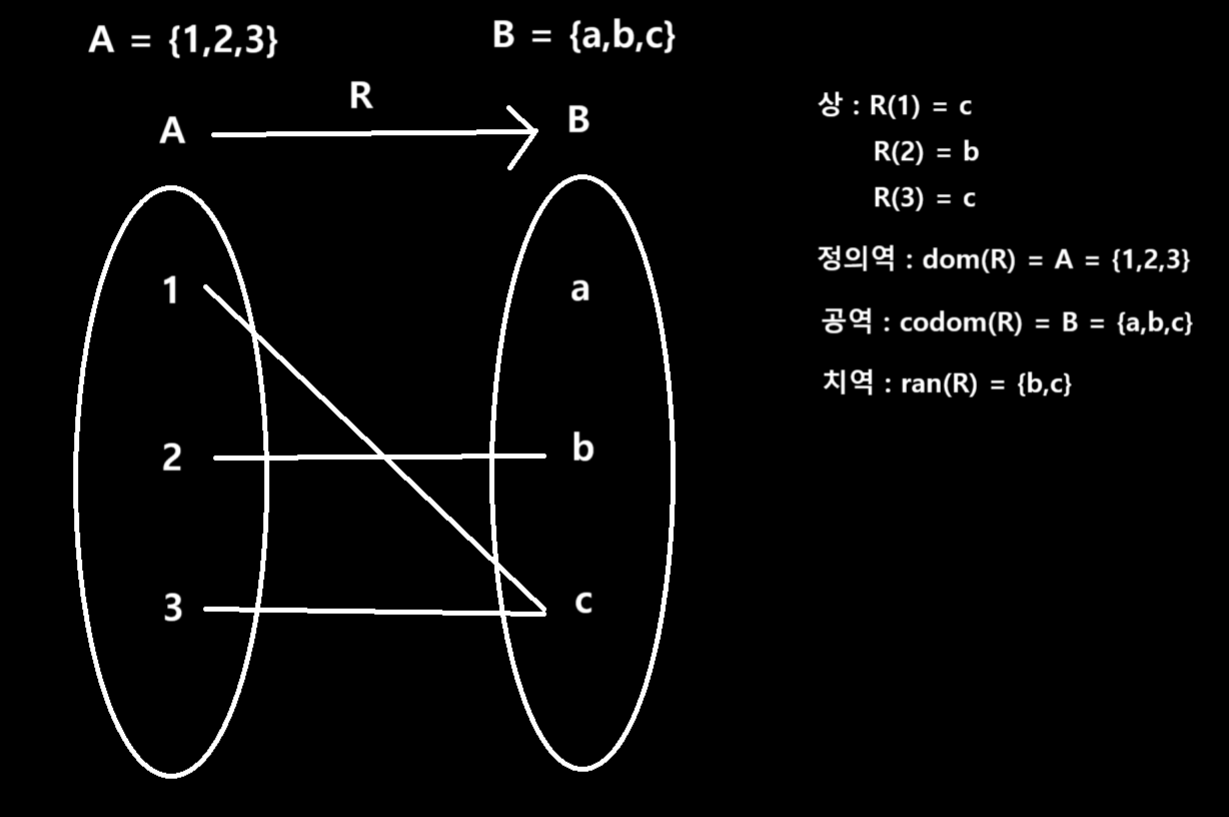
R의 상(Image)

• 이항관계 R에 대해서 집합 A의 원소 a에 대응하는 집합 B의 원소 b를 상이라 정의
• R(a) = b로 표기

R의 정의역(Domain)

• 이항관계 R에 대해서 집합 A를 R의 정의역이라 정의
• dom(R)로 표기

R의 공역(Codomain)

• 이항관계 R에 대해서 집합 B를 R의 정의역이라 정의
• codom(R)로 표기

R의 치역(Range)

• 상의 집합
• ran(R)로 표기

그림으로 보는 상, 정의역, 공역, 치역

---

예제1

A = {1,2,3}, B = {a,b}라 하자. 이때 이항관계 R = {(1,a),(2,b),(3,b),(1,b)}가 A에서 B로의 관계인지 확인하고 R의 상, 정의역, 공역, 치역을 나타내어라

• A에서 B로의 관계인지를 확인하기 위해서는 R이 AxB의 부분집합인지 확인

AxB = {(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)}
따라서, R은 AxB에 대해 부분집합이므로 R은 A에서 B로의 관계
이항관계 R을 그림으로 나타내면...

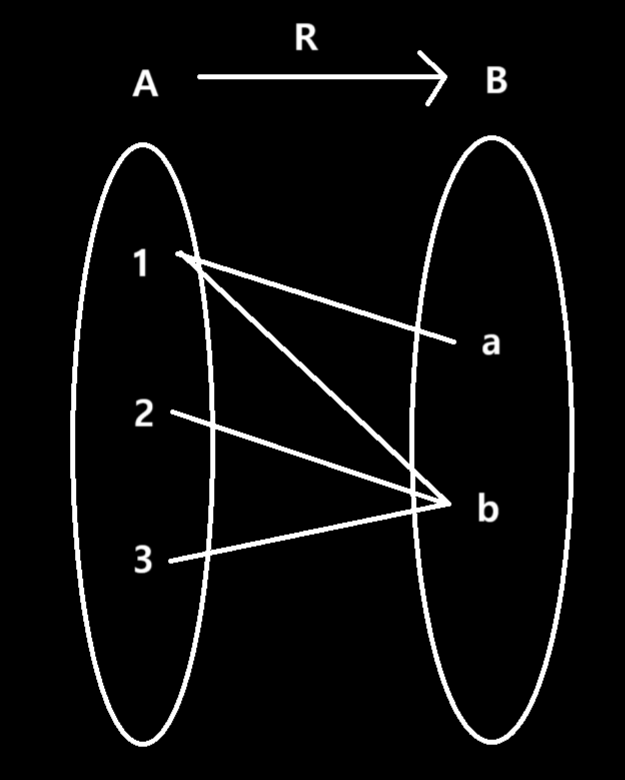
1. 상 : a,b
2. 정의역 : dom(R) = A = {1,2,3}
3. 공역 : codom(R) = B = {a,b}
4. 치역 : ran(R) = {a,b}

A = {1,2,3,4,5}라 하자. A에서 A로 가는 관계 R을 aRb $\iff$ a<b로 정의할 때, R을 구하고 정의역, 공역, 치역을 구하여라

• A에 관한 관계 R이 a<b를 만족하는 순서쌍 (a,b)이므로
  R = {(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}
  1. 정의역 : dom(R) = {1,2,3,4}
  2. 공역 : codom(R) = {1,2,3,4,5}
  3. 치역 : ran(R) = {2,3,4,5}

A = {2,3,4,7}, B = {2,3,4,5,6}이다. A에서 B로의 관계 R은 b가 a로 나누어 떨어질 때 aRb이다. 이때 R을 구하고 정의역, 공역, 치역을 구하여라

• R은 b가 a로 나누어 떨어질때 나머지가 0인 순서쌍 (a,b)를 구하면 된다.
  R = {(2,2),(2,4),(2,6),(3,3),(3,6),(4,4)}
  1. 정의역 : dom(R) = {2,3,4}
  2. 공역 : codom(R) = B = {2,3,4,5,6}
  3. 치역 : ran(R) = {2,3,4,6}

---

집합 사이의 관계를 표시하는 방법

• 화살표 그림(Arrow Diagram)
• 관계 행렬(Relation Matrix)
• 유향 그래프(Directed Graph)

화살표 그림(Arrow Diagram)

• 서로 다른 두개의 구역에 각각 A의 원소와 B의 원소를 써 넣은 후 R의 관계가 있으면 a로부터 B로 화살표를 그리는 방법

A = {2,3,4,7}, B = {2,3,4,5,6}이고, A에서 B로의 관계 R이 R = {(2,2),(2,4),(2,6),(3,3),(3,6),(4,4)}일때 화살표 그림으로 나타내어라

관계 행렬(Relation Matrix)

• 관계 행렬 = 부울행렬(원소가 0,1로만 구성된 행렬)
• 집합 A와 B를 m개와 n개의 원소를 가진 유한집합
• R을 A에서 B로의 관계라고 할 때, R을 다음과 같은 정의에 의해서
  m x n 행렬 $M_R(=M_{ij})$로 바꾸어 쓸 수 있다.
• 단, $M_{ij}$ = 1, ($a_i,b_j)$∈R or 0, ($a_i,b_j)$$\notin$R
  여기서, i = 1,2,3, ... ,m이고 j = 1,2,3, ... ,n

A = {1,2,3}, B = {a,b}일 때, A에서 B로의 관계 R이 R = {(1,a),(2,b),(3,b),(1,b)} 일때 관계 행렬로 나타내어라

따라서 $M_R$은

유향 그래프(Directed Graph)

• 방향을 가진 그래프, 방향 그래프라고도 함
• 관계를 유향 그래프로 표시하기 위해서는 A에서 A로 가는 관계인 A에 관한 관계일때만 가능
• R을 A에서 A로의 관계라 하자
• A의 원소를 정점(Node, Vertex)을 점으로 표기
• 각 원소와 대응되는 정점은 $a_i$와 $a_j$등으로 표시
• $a_{i}$ $R$ $a_{j}$ $((a_{i},a_{j})∈R)$이면 정점 $a_i$에서 정점 $a_j$까지의 방향을 갖는 간선(Edge)으로 묶음

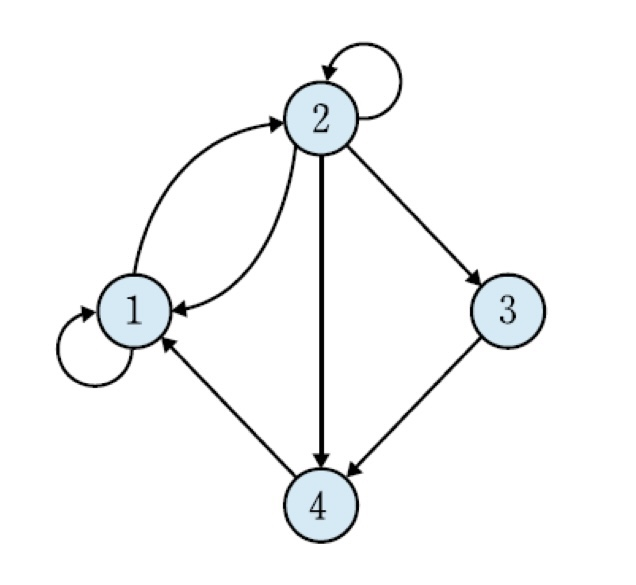
A = {1,2,3,4}에 관한 R이 다음과 같을 때, 유향 그래프를 그려라
R = {(1,1),(1,2),(2,1),(2,2),(2,3),(2,4),(3,4),(4,1)}

• A에 모든 원소들을 노드로 표시하고 관계 R이 있으면 간선을 그림
  

유향 그래프의 내차수,외차수(In-Degree, Out-Degree)

• 내차수(In-Degree)
  노드에 인접한 머리 끝부분의 수
  즉, 노드로 들어가는 간선의 수
• 외차수(Out-Degree)
  노드에 인접한 꼬리 끝부분의 수
  즉, 노드에서 나오는 간선의 수

그래프 각 노드의 내차수(In-Degree), 외차수(Out-Degree)를 구하시오

노드1의 내차수 3, 외차수 2
노드2의 내차수 2, 외차수 3
노드3의 내차수 1, 외차수 1
노드4의 내차수 2, 외차수 2

---

예제2

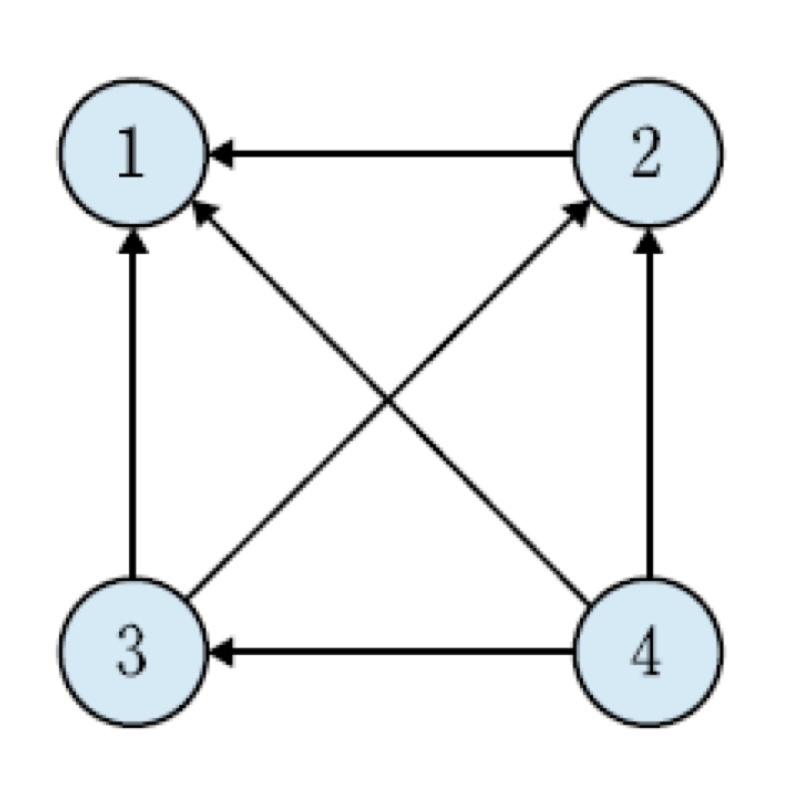
X = {1,2,3,4}, R = {(x,y) | x>y}라 할 때, R을 유향 그래프와 관계 행렬로 표현하라

• R의 조건에 만족하는 관계를 구하면 다음과 같다.
  R = {(2,1),(3,1),(3,2),(4,1),(4,2),4,3)}
  
  
• 유향 그래프
  
  노드1의 내차수 3, 외차수 0
  노드2의 내차수 2, 외차수 1
  노드3의 내차수 1, 외차수 2
  노드4의 내차수 0, 외차수 3
  
  
• 관계 행렬
  

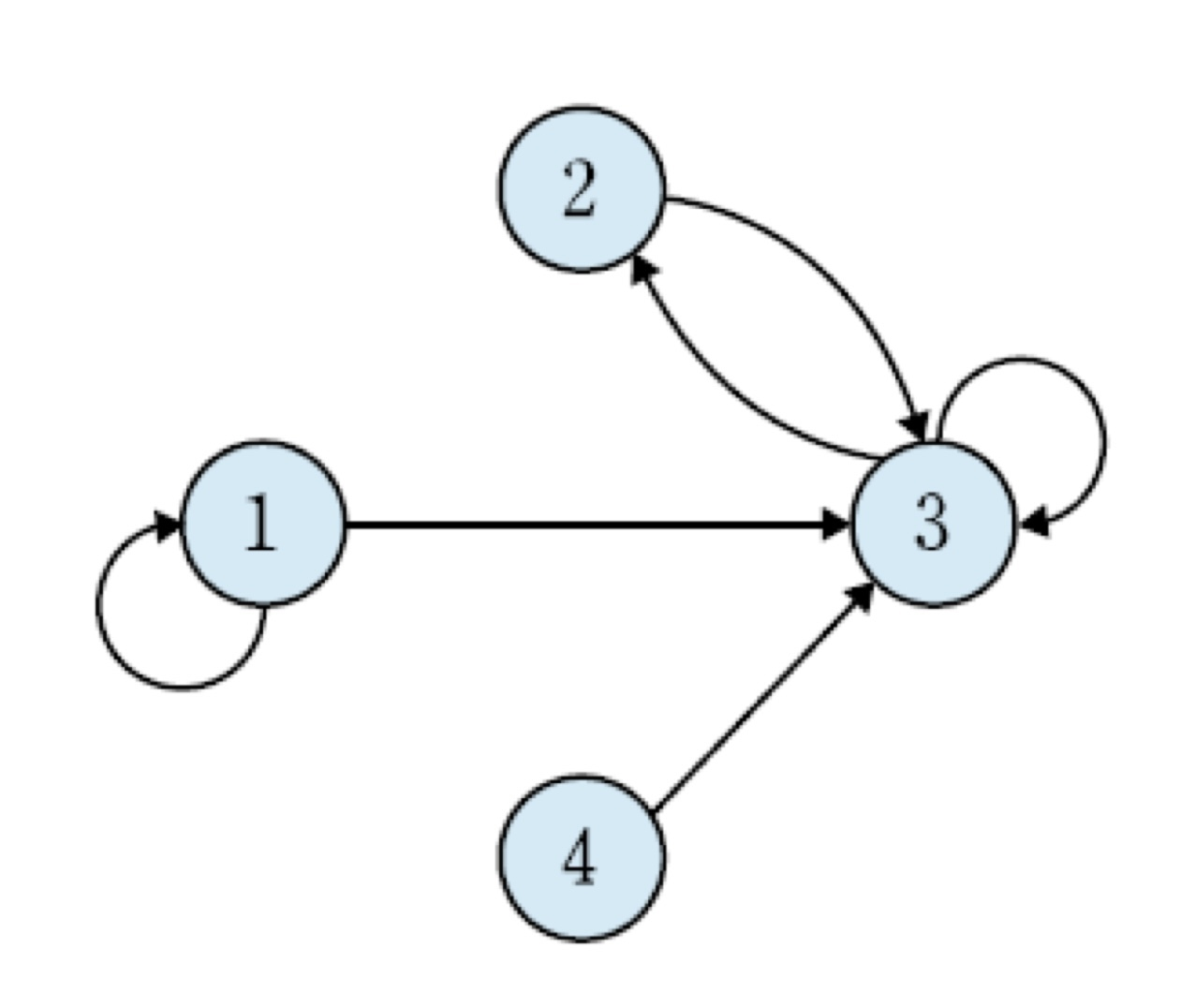
관계가 다음과 같이 유향 그래프로 표시되어 있다. 이때 관계 R을 구하여라.

• 노드1 = {(1,1),(1,3)}
  노드2 = {(2,3)}
  노드3 = {(3,2),(3,3)}
  노드4 = {(4,3)}
  
  R = {(1,1),(1,3),(2,3),(3,2),(3,3),(4,3)}