0. Node embedding 복습
정의 내려야 할 것 3가지
- 인코더 함수 :
- 그래프에서의 유사도 정의
- 임베딩 공간에서의 유사도 정의
그래프에서의 유사도는 랜덤워크나 딥워크 등을 통해 정의할 수 있다. 임베딩 공간에서의 유사도는 두 벡터의 내적으로 간주했다(이를 디코더라고 부르기로 함).
인코더 함수의 경우 앞서 Shallow Encoding을 통해 구현하였는데, 여기에는 몇가지 문제점이 있다.
- 각 노드 별로 개별적인 임베딩 벡터를 가지다 보니 노드의 수가 매우 많아진다면 파라미터의 수가 기하급수적으로 늘어나게 된다.
- 흑습 시 사용되지 않은 노드는 Look-up table에 존재하지 않기 때문에 inference과정에서 사용할 수 없다.
- 노드의 변수들이 사용되지 않는다. (그래프의 구조적 정보만 활용함)
1. Deep Graph Encoders : GNN
GNN은 그래프에 직접 적용할 수 있는 신경망이다. 점 레벨에서, 선 레벨에서, 그래프 레벨에서의 예측 작업에 쓰인다.
유사도는 랜덤워크나 딥워크와 같이 지금까지 사용한 유사도와 같지만, encodr의 구조는 달라진다. cnn, rnn, dnn 등의 딥러닝 방법론들을 차용하여 multiple layers of non-linear transformations based on graph structre를 구성하게 된다.
GNN의 핵심은 점이 이웃과의 연결에 의해 정의된다는 것이다. 연결관계와 이웃들의 상태를 이용하여 각 점의 상태를 업데이트(학습)하고 마지막 상태를 통해 예측 업무를 수행한다. 그리고 마지막 상태가 'node embedding'이 된다.
1-1. GNN이 해결할 수 있는 문제
- Node Classification (Node embedding을 통해 점들을 분류하는 문제)
- Link Prediction (그래프의 두 점 사이에 얼마나 연관성이 있을지 예측하는 문제)
- Community detection (밀집되어 연결된 노드의 클러스터들을 식별)
- Network similarity (두개의 (sub)networks들이 얼마나 비슷한지)
1-2. Notation
- : vertex set, 노드 집합
- : adjacency matrix, 인접행렬
- : 의 어떤 한 노드
- : 노드 v의 이웃노드 집합
- : 노드 변수들 (노드의 변수가 없다면 indicator vectors 또는 Vector of constant 1: [1,1, ... , 1] 사용)
2. Graph Convolution Networks
CNN의 방법론을 차용하여 그래프에 접목한 GCN
2-1. How to propagate information across the graph to compute node features
GCN은 기존의 딥러닝 모델과 다르게 순전파의 과정이 다음의 두 과정을 거치게 된다. (손실함수 계산이나 역전파 과정은 동일하다.)
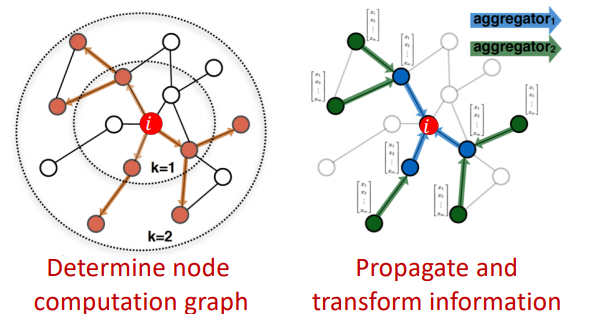
1) 각 노드 별 계산 그래프 생성
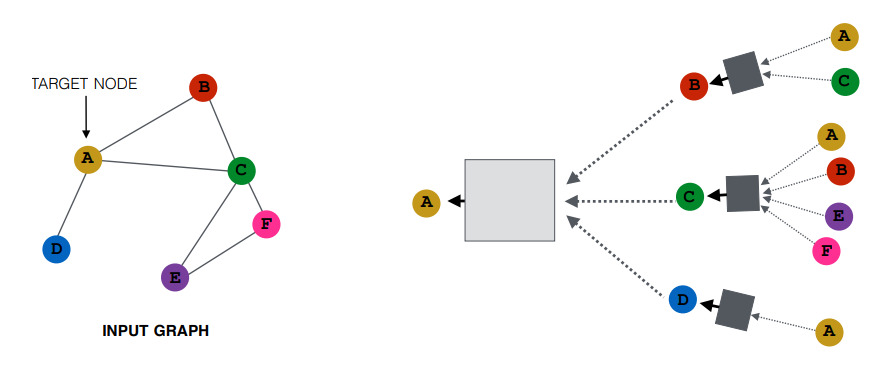
타겟 노드 A에 대한 2 hope node 까지의 계산 그래프에 대한 그림이다. A는 이웃 노드 B , C, D 로부터 정보를 받고 각각의 이웃노드 B, C, D는 또다시 그들의 이웃 노드로부터 정보를 받는다. 계산 그래프의 오른쪽에서 왼쪽으로 정보가 흐른다.

모든 노드에 대한 계산 그래프를 표현한 그림이다. 각 노드마다 각기 다른 형태의 계산 그래프의 형태를 갖고 있다. 넓은 형태의 계산 그래프가 존재하기도 하고 좁은 형태의 계산 그래프도 존재한다. E 와 F의 경우에는 동일한 형태의 계산 그래프를 갖고 있다. 즉 두 노드는 동일한 모델을 통해 처리될 수 있다.
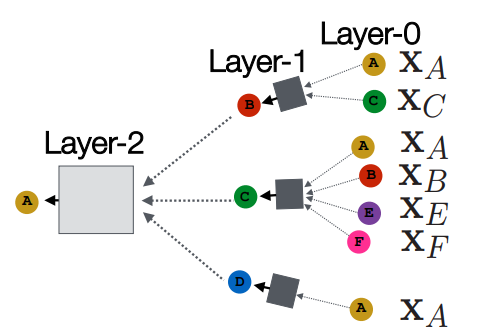
Layer0 에서의 노드들의 정보가 합쳐져(aggregate) Layer1으로 전달되고 해당 층에 있는 노드의 임베딩 벡터와 연산을 거쳐서 Layer2로 전달이 된다. 유의할 점은 동일한 노드더라도 Layer0 에서의 임베딩 벡터와 Layer1에서의 임베딩 벡터는 다르다.
2) 순전파, Neighborhood Aggregation
각 레이어는 어떻게 이웃 노드들의 정보를 모을까? 가장 적합하면서 단순한 연산은 평균/합이다.
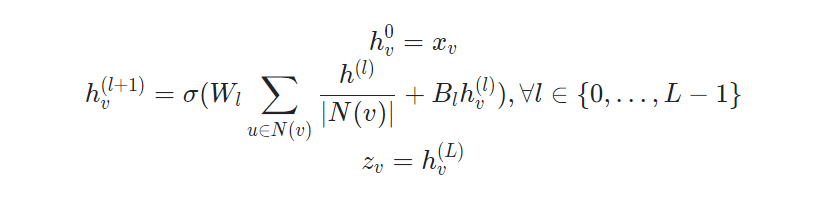
첫 번째 hidden layer의 입력값은 각 노드의 변수벡터 혹은 임베딩 벡터이다.
두 번째 히든 레이어부터 마지막 히든 레이어까지는 각 레이어의 이웃노드의 벡터의 평균과 이전 레이어의 해당 노드를 선형 변환한 것을 결합하여 활성화 함수를 통과한 값이다.
파라미터는 과 두 행렬이 전부다. 즉 모든 계산 그래프는 동일한 가중치를 공유한다.
3) Matrix Formulation
연산을 행렬단위로 하면 훨씬 효율적인 계산이 가능하다.
- Let : 번째 레이어의 모든 노드들의 벡터를 concat하여 행렬로 표현할 수 있다. shape은 (노드, 차원) .
- Then : : 와 인접행렬의 연산은 모든 이웃 노드 벡터들의 합이 된다.
- : 는 대각행렬이고 각 대각 성분은 노드의 이웃노드의 수를 갖는다고 하면, 대각행렬 의 역행렬은 노드의 이웃노드 수의 역수가 된다.
위 세가지를 이용하면,
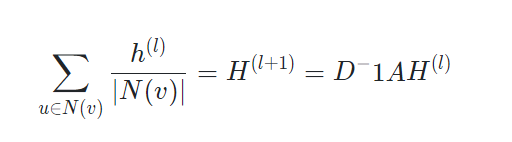
그리고 식을 완전히 정리하면,
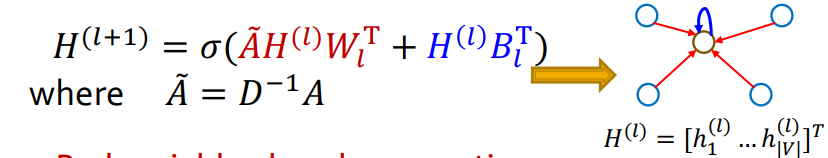
위 그림과 같이 된다.
3. GNN의 학습 과정
지금까지 살펴본 과정들의 결과물은 , 임베딩 벡터이다. 이를 학습하기 위해서는 손실함수를 정의하고 최적화를 진행해야 한다. 학습 과정은 지도학습, 비지도학습 모두 사용 가능하다.
1) 비지도 학습
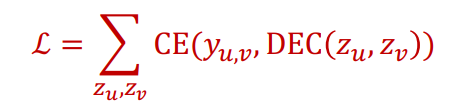
비지도 학습에서의 손실함수는 위와 같다. 유사도는 랜덤워크 등의 방법이 사용되고, 디코더는 내적이 사용된다.
는 노드가 유사할 경우 1, 아닐 경우는 0을 나타낸다. 디코더 또한 유사할 경우에는 1, 그렇지 않으면 0을 계산하도록 파라미터가 최적화된다.
2) 지도학습
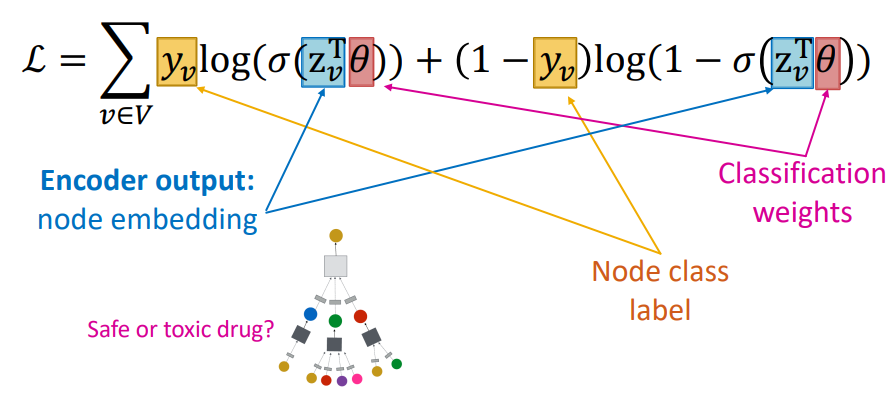
지도학습에서의 손실함수는 위와 같다. 지도학습은 각 노드의 레이블을 예측하는 방식으로 손실함수를 구현한다.
4. Model Design
전체적인 GNN 모델의 과정을 요약하면 다음과 같다.
- Define a neighborhood aggregation function
- Define a loss function on the embeddings
- Train on a set of nodes ( a batch of compute graphs)
- Generate embeddings for nodes as needed
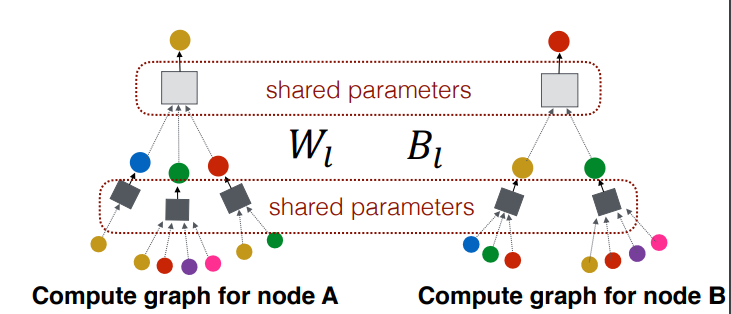
GNN에서 주목할만한 점은 모든 계산그래프에서 구조에 상관 없이 파라미터가 공유된다는 점이다. 이는 학습에 사용되지 않았던 노드들도 추가학습 없이 임베딩 벡터를 효과적으로 생성할 수 있는 능력을 GNN모델은 갖추었다고 할 수 있다.
