[알고리즘] Minimum Spanning Tree

우노·2024년 5월 10일

Algorithm

목록 보기

8/10

Spanning Graph = 모든 노드를 포함하는/연결하는 부분 그래프
Spanning Tree = 트리이므로 Spanning Graph - Cycle
즉, 임의의 그래프에서 사이클이 없고 모든 노드를 포함하도록 간선을 일부 선택하여 만든 부분 그래프를 의미한다.

Minimum Spanning Tree = Spanning Tree 중 가중치가 최소인 그래프

Kruskal, Prim 두 알고리즘 예제로는 프로그래머스 섬 연결하기 문제를 선택했다.

두 알고리즘 모두 무방향 가중치 연결 그래프를 전제로 한다.

Kruskal

크루스칼 알고리즘은 간선 중심으로 설계 관점에서 그리디이다.

모든 간선을 포함한 집합에서 가중치가 작은 순서대로 확인하며 포함
1. 사이클을 생성하지 않으면 포함
2. 사이클을 생성하면 제외
모든 간선을 포함한 상태에서 가중치가 큰 순서대로 확인하며 제외
1. 해당 간선을 제외했을 때 그래프를 둘로 분리하지 않으면 제거
2. n-1개의 변이 남을 때까지 반복 (사이클을 생성하지 않으려면 n-1개의 변이 필요하다.)

1.을 기준으로 로직을 간단히 적어보면 다음과 같다.

로직

모든 간선을 포함한 집합 S를 준비한다.

S에서 가중치가 작은 순서대로 확인한다.

해당 간선이 사이클을 생성하면 제외한다.

그렇지 않으면 해당 간선을 포함한다.

S에 간선이 남지 않을 때까지 (n-1개의 간선이 포함될 때까지) 2. 를 반복한다.

섬 연결하기 문제를 예시로 들자면

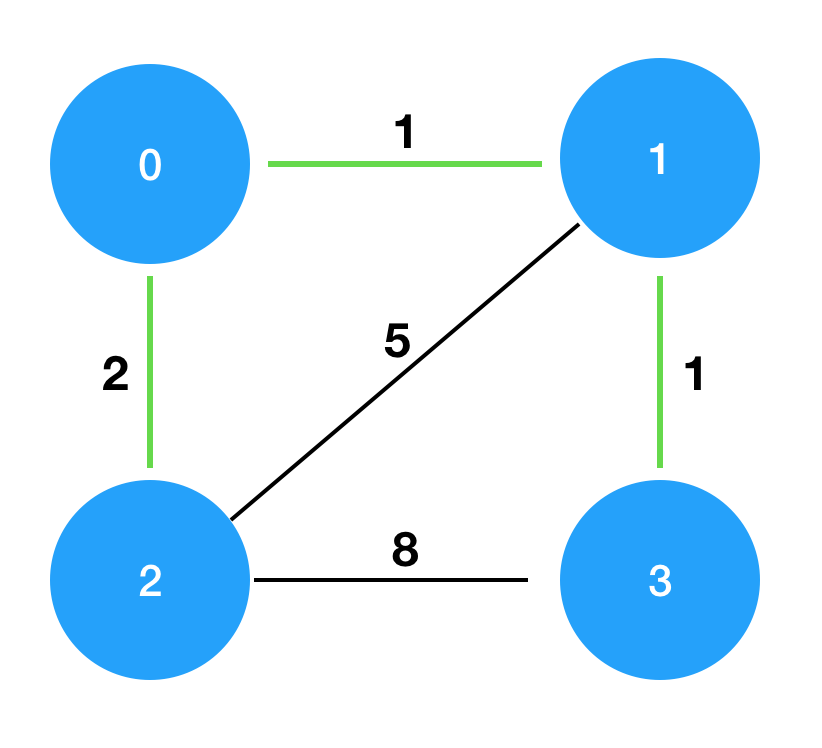
[[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 가중치 순으로 정렬 또는 우선순위큐에 삽입
➡️ [[0,1,1], [1,3,1], [0,2,2], [1,2,5], [2,3,8]] 순서대로 확인
[0,1,1] - 포함 ➡️ [1,3,1] - 포함 ➡️ [0,2,2] - 포함
➡️ [1,2,5] - 제외 ➡️ [2,3,8] - 제외
(n-1개의 간선을 포함하면 중지해도 된다.)

알고리즘은 간단하지만 사이클을 갖지 않는다는 점을 효율을 챙기면서 코드로 확인하기는 쉽지 않다.

#include <string>
#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

vector<int> island(101);

bool cmp(vector<int> a, vector<int> b){
    return a[2] < b[2];
}

int findParent(int idx){
    if(island[idx] == idx)
        return idx;
    return island[idx] = findParent(island[idx]);
}

int solution(int n, vector<vector<int>> costs) {
    int answer = 0;
    
    //섬 저장
    for(int i=0; i<n; i++){
        island[i] = i;
    }
    // 1. 비용이 적은순으로 정렬
    sort(costs.begin(), costs.end(), cmp);
    
    for(int i=0; i<costs.size(); i++){
        int start = findParent(costs[i][0]);
        int end = findParent(costs[i][1]);
        int cost = costs[i][2];
        
        //2. cycle이 만들어지지 않으면 다리 추가
        if(start!=end){
            answer+=cost;
            island[end] = start;
        }
    }

    return answer;
}

O(E\;logE)

최적은 $O(E \;logV)$ 이며 $O(E\;logE)$ 도 가능하다.
코드 출처: [프로그래머스] 섬 연결하기 (C++)

Prim

프림 알고리즘은 정점 중심으로 설계 관점에서 그리디이다.

로직

모든 간선을 포함한 집합 S1를과 빈 집합 S2를 준비한다.

임의의 정점을 선택하여 방문 처리하고 S2에 삽입한다.

S2에 있는 정점 중 방문하지 않은 정점 중에서 가장 낮은 가중치의 간선을 갖는 정점을 선택한다.

해당 정점을 방문 처리하고 지금까지 방문한 정점에 연결된 간선들을 비교하여 3. 수행을 반복한다.

모든 정점이 방문 처리될 때까지 3. 을 반복한다.

3-a. 에서 현재까지 방문한 모든 정점에 연결된 간선들의 가중치를 비교하면서 지속적으로 원소 삽입과 정렬이 이루어지기 때문에 우선순위 큐를 활용하면 시간복잡도가 효율적이다.

정점 0 선택 ➡️ 우선순위 큐에 (1, 1), (2, 2) 삽입 ⚡[(1, 1), (2, 2)]

➡️ 정점 1 선택 ➡️ 우선순위 큐에 (2, 5), (3, 1) 삽입 ⚡[(3, 1), (2, 2), (2, 5)]

➡️ 정점 3 선택 ➡️ 우선순위 큐에 (2, 8) 삽입 ⚡[(2, 2), (2, 5), (2, 8)]

➡️ 정점 2 선택 ➡️ 모든 정점 선택 완료하여 종료

#include <string>
#include <vector>
#include <queue>

using namespace std;

int solution(int n, vector<vector<int>> costs) {
    int answer = 0, v = 0, node = 0, c = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;      // 가중치, 정점
    vector<bool> visited(n, false);
    vector<int> a(n, -1);
    vector<vector<int>> adj(n, a);
    
    if(n == 1)
        return 0;
    
    for(auto c:costs){
        adj[c[0]][c[1]] = c[2];
        adj[c[1]][c[0]] = c[2];
    }
    
    pq.push({0, 0});
    while(v < n){
        c = pq.top().first;
        node = pq.top().second;
        pq.pop();
        
        if(visited[node])
            continue;
        visited[node] = true;
        v++;
        answer += c;
        
        for(int i=0; i<n; i++){
            if(adj[node][i] > 0 && !visited[i])
                pq.push({adj[node][i], i});
        }
    }
    
    return answer;
}