[알고리즘] Shortest Path

우노·2024년 5월 6일
알고리즘
0

Algorithm

목록 보기
7/10

최단 거리는 또 다른 최단 거리의 집합임을 알고 시작하자 ❕
최단 거리를 쌓아서 최단 거리 업데이트 → 다시 쌓고 업데이트 → …
⇒ Dynamic Programming 활용한다.

Dijkstra

하나의 시작 노드를 설정하여 각 노드까지의 최단 거리를 구하는 알고리즘
⚠️ 음의 가중치가 없는 그래프에서 유효

설계 관점에서 방문하지 않는 노드 중 가장 거리가 작은 노드 선택을 반복
⚡Greedy로 설명할 수 있다 !

로직

  1. 하나의 시작 노드를 선택하고 나머지 노드들까지의 거리를 INF로 설정한다. (방문하지 않음을 표시)

  2. 현재 선택된 노드에서 인접한 노드들의 거리를 확인한다.

    • 시작 노드 → 인접 노드
    • (시작 노드 → 현재 선택 노드) + (현재 선택 노드 → 인접 노드)

    를 비교하여 둘 중 작은 값으로 업데이트한다.

  3. 현재 선택된 노드를 방문 처리하고 방문하지 않는 노드들 중 거리가 최소인 노드를 선택한다.

  4. 모든 노드를 방문할 때까지 2. ~ 4.를 반복한다.

구현: 선형 탐색, 우선순위 큐 등

프로그래머스 배달 문제로 코드 예시를 들어 설명해보자.
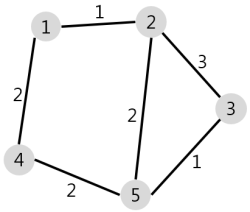시작 노드: 1번 마을

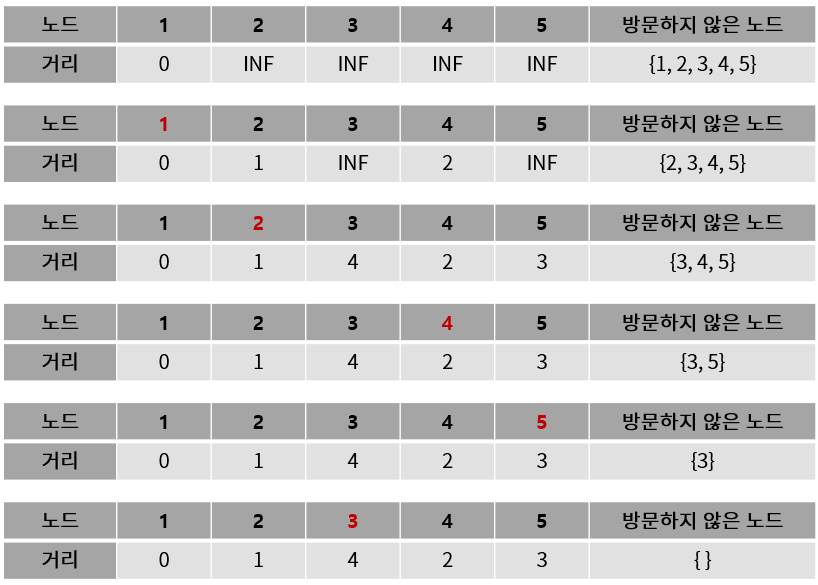
  1. 거리 테이블 초기화 (시작 노드: 0 / 나머지: INF)
  2. 인접 노드 거리 업데이트
    → 방문하지 않은 노드 중 가장 작은 2번 노드 선택
  3. 3번 노드 1+3<INF 업데이트 & 5번 노드 1+2<INF 업데이트
    → 4번 노드 선택
  4. 5번 노드 2+2>3 이므로 업데이트하지 않음
    → 5번 노드 선택
  5. 3번 노드 3+1==4 이므로 업데이트X → 3번 노드 선택
    2번 ↔ 3번 간선도 존재하지만 2번은 방문하여 이미 고려된 케이스이기 때문에 무시
    결론적으로 방문하지 않은 노드들만 고려하여 계산
  6. 모든 노드를 방문했으므로 종료

선형 탐색

정점은 많은데 간선은 적을 때 치명적 (모든 정점을 반복해서 확인함)

#include <vector>

using namespace std;

int solution(int N, vector<vector<int>> road, int K) {
    int answer = 0, node = 1, v = 0;
    vector<int> cost(N+1, 500001);
    vector<vector<int>> adj(N+1, cost);;
    vector<bool> visited(N+1, false);
    
    for(int i=0; i<road.size(); i++){
        if(adj[road[i][0]][road[i][1]] > road[i][2]){
            adj[road[i][0]][road[i][1]] = road[i][2];
            adj[road[i][1]][road[i][0]] = road[i][2];
        }
    }
    
    cost[1] = 0;
    while(true){
        int min = 500001;
        visited[node] = true;
        
        for(int i=2; i<=N; i++){
            if(!visited[i] && adj[node][i] < 500001)
                cost[i] = cost[i] < cost[node] + adj[node][i] ? cost[i] : cost[node] + adj[node][i];
        }
        
        for(int i=2; i<=N; i++){
            if(!visited[i] && cost[i] < min){
                min = cost[i];
                node = i;
            }
        }
        
        if(min == 500001)
            break;
    }
    
    for(int i=1; i<=N; i++){
        if(cost[i] <= K)
            answer++;
    }
     
    return answer;
}
O(N∗(2∗N)+N)=O(N2)      (N=Vertex)O(N*(2*N)+N) = O(N^2)\;\;\;(N=Vertex)

우선순위 큐

최단 거리를 계산해야하므로 작은 값을 우선으로 정렬

#include <vector>
#include <queue>

using namespace std;

int solution(int N, vector<vector<int>> road, int K) {
    int answer = 0, node = 1, v = 0;
    vector<int> cost(N+1, 500001);
    vector<vector<int>> adj(N+1, cost);
    vector<bool> visited(N+1, false);
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
    
    for(int i=0; i<road.size(); i++){
        if(adj[road[i][0]][road[i][1]] > road[i][2]){
            adj[road[i][0]][road[i][1]] = road[i][2];
            adj[road[i][1]][road[i][0]] = road[i][2];
        }
    }
    
    cost[1] = 0;
    q.push({1, 0});
    while(!q.empty()){
        int idx = q.top().first;
        int dis = q.top().second;
        q.pop();
        
        if(visited[idx] || cost[idx] < dis)
            continue;
        
        for(int i=2; i<=N; i++){
            if(!visited[i] && cost[i] > cost[idx] + adj[idx][i]){
                cost[i] = cost[idx] + adj[idx][i];
                q.push({i, cost[i]});
            }
        }
    }
    
    for(int i=1; i<=N; i++){
        if(cost[i] <= K)
            answer++;
    }
     
    return answer;
}
O(logN∗N)=O(N logN)    (N=Vertex)O(logN *N) = O(N\ logN) \;\;(N=Vertex)

선형 탐색이 직관적이지만 다음 방문 노드 선택을 포함해서 우선순위 큐가 더 효율적

Bellman-Ford

다익스트라와 동일한 알고리즘을 수행
ㄴ 하나의 시작 노드를 설정하여 각 노드까지의 최단 거리를 구하는 알고리즘

실행 속도 | 다익스트라 < 벨만-포드
vs Dijkstra | 가중치가 음수인 경우도 처리 가능 !

다익스트라는 가중치가 음수인 경우에 최솟값 갱신→ 사용 불가 ⛔
벨만 포드는 가중치가 가중치가 음수여도 최적의 값 탐색

🚨 하지만 음수 사이클이 생기면 다익스트라와 동일하게 최솟값이 갱신되어 사용 불가 ⛔

설계 관점에서 Dynamic Programming으로 설명할 수 있다 !

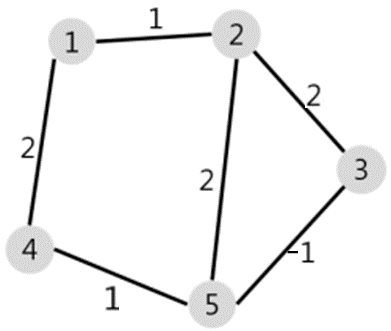다음과 같은 경우에 1 → 3의 실질적 최솟값은 2
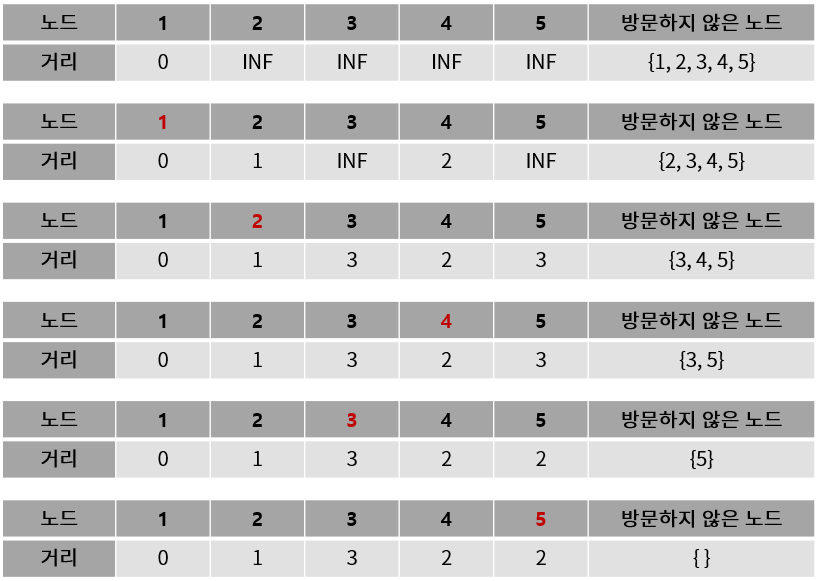하지만 다익스트라로 구하면 위와 같이
3이 이미 방문한 노드이므로 5 → 3이 무시되어 1 → 3의 최솟값이 3으로 계산된다.
벨만 포드는 방문과 관계 없이 정점마다 모든 간선을 확인하여 이를 방지한다.

로직

  1. 하나의 시작 노드를 선택하고 나머지 노드들까지의 거리를 INF로 설정한다.
  2. 모든 간선을 돌며 노드들의 거리를 확인한다.
    • 시작 노드 → 간선 끝 노드
    • (시작 노드 → 간선 시작 노드) + (간선 시작 노드 + 간선 끝 노드)
      를 비교하여 둘 중 작은 값으로 업데이트한다.
  3. (노드 수)-1만큼 2. 를 반복한다.
  4. 음수 사이클 존재 여부 확인 후, 없으면 결과 반환 (있으면 비유효한 결과값)
  1. 에서 (노드 수)-1 만큼 반복하는 이유는
    [ 시작 노드 → 임의의 노드 ] 의 사이에 거칠 수 있는 간선의 최대 개수가
    (노드 수)-1 이기 때문이다.
  2. 에서 음수 사이클의 존재 여부는 3. 종료 후에 2. 과정을 한 번 더 수행했을 때
    테이블 값이 업데이트 되는지에 따라 판별할 수 있다.

(3. 에서 노드 수로 수행해도 되며 (노드 수)-1 이후에는 음수 사이클이 없는 경우 전부 최솟값으로 세팅되어 더이상 업데이트 되지 않기 때문이다.
마찬가지로 4.에서 갱신 여부만 확인하면 된다.)

위 로직에서 알 수 있 듯 벨만-포드의 최적 시간복잡도는 다음과 같다.

O((V−1)∗E)=O(VE)O((V-1)*E) = O(VE)

다음은 프로그래머스 배달 문제에서 벨만-포드를 활용한 예시이다. 무방향 그래프이므로 양방향을 모두 고려해주어야한다. 
#include <vector>

using namespace std;

int solution(int N, vector<vector<int>> road, int K) {
    int answer = 0;
    vector<int> cost(N+1, 500001);
    
    cost[1] = 0;
    for(int i=2; i<=N; i++){
        for(int j=0; j<road.size(); j++){
            if(cost[road[j][1]] > cost[road[j][0]] + road[j][2])
                cost[road[j][1]] = cost[road[j][0]] + road[j][2];
            if(cost[road[j][0]] > cost[road[j][1]] + road[j][2])
                cost[road[j][0]] = cost[road[j][1]] + road[j][2];
        }
    }
    
    for(int i=1; i<=N; i++){
        if(cost[i] <= K)
            answer++;
    }
    
    return answer;
}

Floyd-Warshall

가능한 모든 노드 쌍에 대해서 최단 거리를 구하는 알고리즘
⚠️ 가중치의 음/양은 상관이 없지만 음수 사이클은 없어야 함

vs Bellman-Ford |
벨만 포드는 시작 노드 → 나머지 노드 를 계산
플로이드 워셜은 모든 노드 쌍에 대해서 계산 (A → B, B → A 자동으로 고려됨)

설계 관점에서 Dynamic Programming으로 설명할 수 있다 !

로직

  1. 하나의 시작 노드를 선택하고 나머지 노드들까지의 거리를 INF로 설정한다.
  2. 임의의 노드를 중간 노드(i)로 설정한 경우에 대하여 다음을 수행한다.
    임의의 노드 j - 시작 노드 / 임의의 노드 k - 끝 노드
    • j → k
    • j → i + i → k
      를 비교하여 둘 중 작은 값으로 업데이트한다.
    • 가능한 모든 (j, k)에 대해서 수행을 반복한다.
  3. 2.를 모든 노드에 대해서 수행을 반복한다.

플로이드-워셜은 거리와 관계없이 시작→끝 으로 가는 모든 경우를 탐색하고
최솟값인 경우에만 업데이트한다.

위 로직에서 알 수 있 듯 플로이드-워셜의 최적 시간복잡도는 다음과 같다.

O(N3)    (N=Vertex)O(N^3) \;\;(N=Vertex)

다음은 프로그래머스 배달 문제에서 플로이드-워셜을 활용한 예시이다. 
#include <vector>

using namespace std;

int solution(int N, vector<vector<int>> road, int K) {
    int answer = 0, idx;
    vector<int> r(N+1, 20000001);
    vector<vector<int>> adj(N+1, r);
    vector<bool> visited(N+1, false);
    
    for(int i=0; i<road.size(); i++){
        if(adj[road[i][0]][road[i][1]] > road[i][2]){
            adj[road[i][0]][road[i][1]] = road[i][2];
            adj[road[i][1]][road[i][0]] = road[i][2];
        }
    }
    for(int i=1; i<=N; i++){
        adj[i][i] = 0;
    }
    
    for(int i=1; i<=N; i++){
        for(int j=1; j<=N; j++){
            for(int k=1; k<=N; k++){
                adj[j][k] = min(adj[j][k], adj[j][i] + adj[i][k]);
            }
        }
    }
    
    for(int i=1; i<=N; i++){
        if(adj[1][i] <= K)
            answer++;
    }
    
    return answer;
}

총정리

정리하자면 음의 사이클이 없는 그래프에 대해서

다익스트라: 시작 노드가 정해져있고 음의 가중치가 없는 경우
벨만-포드: 시작 노드가 정해져있고 음의 가중치가 있는 경우
플로이드-워셜: 시작 노드가 정해져있지 않고 최소 거리를 찾는 경우

위에서부터 차례대로 확인하면서 사용하자 !

profile
우노
기록하는 감자
이전 포스트

[알고리즘] Binary Search

다음 포스트

[알고리즘] Minimum Spanning Tree

0개의 댓글

관련 채용 정보