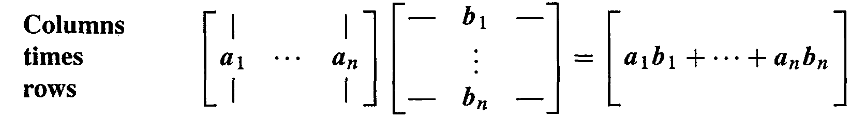#Lec 3. Multiplication and Inverse Matrices

✔ 들어가며

지난 lec 2에서는 Elimination과 elimination matrix, permutation matrix에 대해 공부를 했다. 그리고 마지막 부분에서 inverse matrix에 대해서 간략히 알아보았다. 이번 강의는 inverse matrix에 대해서 조금 더 자세히 살펴볼 예정이다.
하지만 그 전에 먼저 선형대수학에서의 matrix, row vector, column vector들 사이의 multiplication에 대해서 더 이해를 해보자.

☕️ Multiplications

🍪 Method 1: Multiply matrix by matrix

먼저 알아볼 곱셈(Multiplication)은 행렬과 행렬의 곱인 matrix multiplication이다. 가장 간단한 형태이며 이미 모두가 잘 알고 있는 규칙이라고 생각한다.
따라서 일반적인 방법으로 $C = AB$ 행렬 곱을 해서 $C_{34}$의 원소를 구해보자. (아래의 그림을 참고하자.)

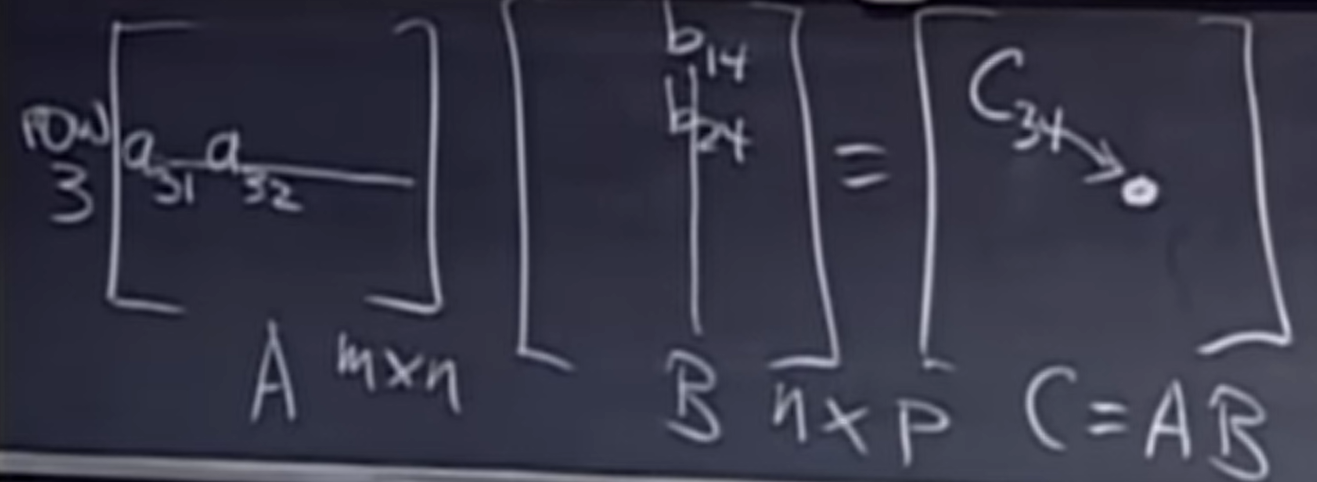
우리가 아는 방법으로 $C$의 원소를 구하는 방법은 원소의 위치에서 행에 해당하는 row를 $A$에서 열에 해당하는 column은 $B$에서 선택해 둘을 내적하면 된다. 즉, 두 벡터 간의 내적으로 구할 수 있는데 $C_{34} = (row_3 \ of\ A)\cdot(column_4 \ of \ B)$와 같이 표현 가능하다.

특히 $row_3$ of $A$와 $col_4$ of $B$의 각 원소 입장에서 보면 또한 다음과 같이 표현가능하다.
$C_{34} = (row_3 \ of\ A)\cdot(column_4 \ of \ B) = a_{31}b_{14} + a_{32}b_{24} + ...$
이 표현은 원소들 곱의 합들로 구해진다. 따라서, $\Sigma_{k=1}^{n} a_{3k}b_{k4}$로도 표현가능하다.

행렬곱에서 중요한 점은 각 행렬의 크기이다. 만약 $A$가 m $\times$ n이라면 m개의 행, n개의 컬럼이 있는거고 이때 $B$는 n개의 행을 가져야만 한다.
또한, 이때 $B$의 col의 갯수가 p개라면 $C$는 m $\times$ p의 크기를 가지게 된다. $\rightarrow$ $A \times B= (m \times n)(n \times p) = (m \times p)$.
$A$, $B$가 둘다 정사각 행렬이라면 $C$역시 동일한 크기를 가진다.

🍪 Method 2 : Multiply matrix by column

이번에 살펴볼 연산은 행렬과 벡터의 곱셈을 통해 행렬 곱 행렬을 이해해볼 것이다. 즉, 연산을 column vector의 입장에서 바라보자. 우리는 이미 lec 2에서 행렬 곱 column이 column이라는 것을 공부했다.

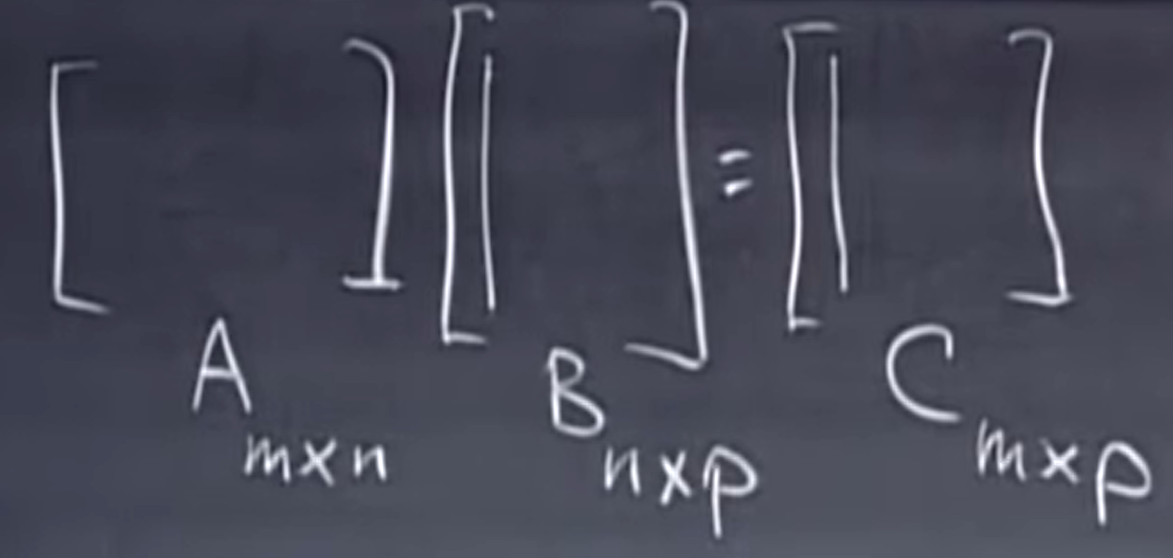
$A\times B=C$에서 하나의 column 입장에서 바라보자. $A \times (column_1\ of\ B) = (column_1\ of\ C)$가 된다. 이는 $A$의 column들의 어떤 linear combination으로 새로운 column이 만들어지는 형태다.
이를 확장해서 $C$의 전체 column들 입장에서 보면 행렬 곱하기 column vector로 나온 결과 column $p$들을 옆으로 나란히 놓은 형태로 생각할 수 있다.
→ $C$의 columns은 $A$의 columns의 linear combination이다. (lec 2 참고)

🍪 Method 3: Multiply row by matrix

이번에는 row 입장에서 생각해보자. row는 column과 다르게 matrix 앞에서 곱해져야한다. multiplication 규칙에 의해 $(m \times n)(1 \times m)$은 계산할 수 없고 $(1 \times m)(m \times n)$와 같이 row 곱 행렬을 해야한다.

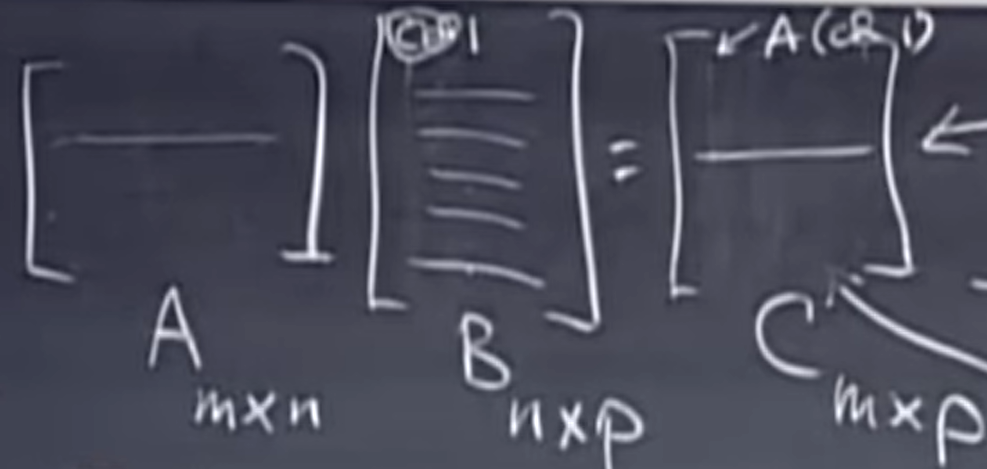
$row\ of\ A$를 모든 $B$의 rows과 곱해 $C$의 새로운 row를 만들 수 있다.
column 입장에서 생각했던 것과 위치만 다를뿐 동일한 형태인 것을 알 수 있다.
또한 lec 2에서 row 곱 행렬을 하면 row가 되는 것을 알고 있기에 조금 직관적이지 않더라도 천천히 생각해보면 금방 이해가 간다.
→ $C$의 rows은 $B$의 rows의 linear combination이다.

🍪 Method 4 : Multiply Column by Row

다른 한가지 방식은 $column \times row$이다. $row \times column$은 하나의 숫자(scalar)로 계산되지만 $column \times row$는 조금 다르다.

예를 들어 아래와 같은 $m \times 1$ 크기의 $A$, $1 \times p$ 크기의 $B$가 있다고 해보자.

$A(3 \times 1) \times B(1 \times 2) = C(3 \times 2)$가 되었고 이는 매우 특별한 행렬이다. 이 행렬은 나중에 배울 rank 1 matrix이고 차차 다루도록하자.

이 행렬의 column들은 $\begin{bmatrix}2 \\ 3 \\ 4\end{bmatrix}$의 배수들이 되며, row들은 $\begin{bmatrix}1 & 6\end{bmatrix}$의 배수들이 된다.

또한 기존의 $AB$로 돌아가면 $C$는 $columns\ of\ A \times rows\ of\ B$의 합이 된다.

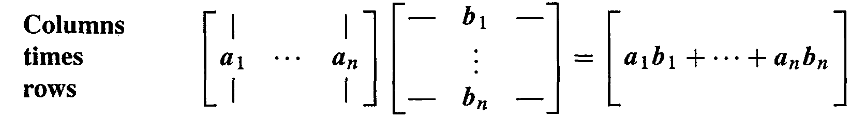
위와 같이 교재에 나온 그림을 통해 행렬 $C$는 특별한 $column \times row$들의 합으로 구성할 수 있다는 점을 이해할 수 있다.

🍪 Method 5 : Block Multiplication

다음으로 알아볼 특징은 행렬 곱에서 행렬을 Block으로 나누어 곱할 수 있다는 것이다. 아래의 그림으로 확인해보자.

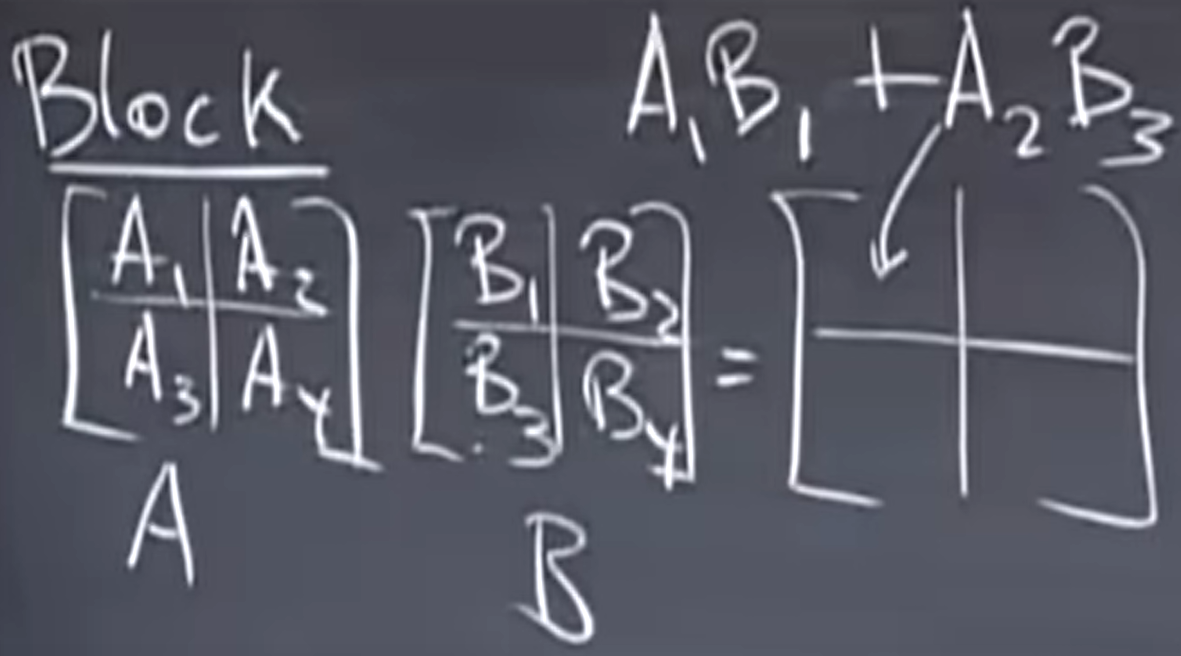
위와 같이 $A$를 $A_1, A_2, A_3, A_4$와 같이 행렬을 자를 수 있고 $B$역시 block 단위로 나눌 수 있다.
이렇게 적절히 잘라진 행렬의 블록들은 기본적인 행렬곱과 동일하게 구하면 된다.
(잘라진 블록들은 크기가 모두 같지 않아도 된다.)
→ Block multiplication은 마치 block rows x block columns와 같이 계산된다.

☕️ Inverse Matrices (Square matrices)

🍪 Inverse Matrix

우선 역행렬이란 어떠한 행렬이 있을때 곱해서 $I$(Identity matrix)가 나오는 행렬을 의미한다. $A$의 inverse matrix(역행렬)은 $A^{-1}$이라고 표기한다.

역행렬은 non-singular case일때 존재하며 invertible하다고 말한다. 즉, 행렬이 invertible하다는 것은 역행렬이 존재하고 non-singular case라는 것이다.
그리고 $A$의 inverse는 왼쪽, 오른쪽 곱의 순서와 상관없이 identity matrix $I$가 된다.

🍪 Singular Matrix (No-inverse matrix)

만약 $A^{-1}$이 존재한다면, A는 invertible하고 non-singular matrix라고 했다. 하지만, 모든 matrices가 inverse를 가지는 것은 아니다.

이때 A의 $col_2$는 $col_1$의 위에 있다. 따라서 Identity matrix를 만들 수 없게 된다. 그 이유는 $col_2$에 어떠한 수를 곱해도 $col_1$의 scalar 배이기 때문에 $\begin{bmatrix} 1\\0 \end{bmatrix}$과 $\begin{bmatrix} 0\\1 \end{bmatrix}$ 같이 서로 방향이 다른 vector를 만들 수가 없기 때문이다.

그리고 $Ax=0$을 만드는 경우가 존재하게 되는데 $x = \begin{bmatrix} -3\\1 \end{bmatrix}$과 같은 경우이다. 이 경우에 계산을 해보면 $Ax=0$이 된다. 이러한 $A$를 singular matrix라고 한다.

다시 정리를 해보면, $Ax = 0$에서 $x$를 $x \ne 0$인 vector라고 가정해보자.
$A^{-1}Ax = Ix = x = 0$ 이기에 $x = 0$이 되어야하는데, 가정에 $x \ne 0$이라고 했기 때문에 모순이 발생한다. 따라서 $A$는 solution이 존재하기 위해서는 inverse matrix가 존재하야하고, $x=0$이 아닌 solution이 존재한다면 $A$를 singular matrix라고 한다.

→ $Ax = 0$를 만족하는 0이 아닌 vector $x$가 있다면 역행렬은 존재하지 않는다.
→ $A$가 invertible하면 $Ax = 0$이 되는 $x$는 0 밖에 없다.

🍪 Calculate Inverse of Matrix

하나의 예시를 통해 inverse matrix를 계산하는 방법을 알아보자.

Determinants를 안다면 그 값이 0이 아니라는 것을 통해 inverse가 있음을 알 수 있다.
Column 입장에서는 2개의 column vectors이 서로 다른 방향을 가르키고 있으므로 모든 b를 만들 수 있다는 점을 확인할 수도 있다.

$A$가 역행렬이 있다면 column 입장에서 해석하여 2차 연립방정식 2개를 푸는 것으로 해석할 수 있다.

→ $A$와 첫번째 column이 $I$의 첫번째 column이 되는 연립방정식

→ $A$와 두번째 column이 $I$의 두번째 column이 되는 연립방정식

→ 따라서 $A \times column \; j \; of \; A^{-1} = column \; j \; of \; I$로 정리할 수 있다.

이렇게 두개의 이차 연립방정식을 푸는 것은 Gaussian Elimination이랑 흡사하게 Gauss-Jordan Elimination으로 해결할 수 있다.

☕️ Gauss-Jordan Elimination to solve Inverse of a matrix

바로 위에서 우리는 $A^{-1}$를 미지수로 두어 2개의 연립 방정식을 풀어보았다. 하지만 2개의 방정식을 한번에 푸는 방법을 소개하려고 한다. Gauss-Jordan elimination이 그 방법이다.

두 방정식은 다음과 같고 각각을 해결할 수 있다면 invertible하고 둘을 한번에 해결하기 위해 augmented matrix를 사용하려고 한다.

$A$와 $I$를 augmented matrix form으로 이어서 쓰면 다음과 같다.

이제 Gaussian Elimination을 진행하면 다음과 같다.

가우스는 여기서 step을 멈추지만 Gauss-Jordan은 윗 방향으로 더 진행 한다.

이렇게 나온 matrix는 좌측은 $I$ 되었고 우측은 $A^{-1}$가 된다.
→ $A^{-1}$와 $A$를 곱하여 확인해보면 $I$가 나옴을 확인할 수 있다!

---

6가지 규칙
다음은 inverse matrix의 몇가지 규칙들이다.

1. n$\times$n 행렬의 elimination이 n개의 pivots를 가진다면 inverse는 존재한다.

2. matrix $A$는 inverse를 2개 가지지 않는다.

   if $BA = I, \ AC = I$ then, $B = C$.

   → left inverse = right inverse

3. $A$가 invertible하면 $Ax=b$의 solution은 하나 ($x = A^{-1}b$)이다.

4. $Ax = 0$를 만족하는 0이 아닌 vector $x$가 있다면 역행렬은 존재하지 않는다.

5. 2 $\times$ 2 행렬에 대해서 $ad-bc$가 0이 아니면 inverse가 존재한다.

   $2 \times 2 \, Inverse : \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}^{-1} = {1 \over {ad-bc}} \begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix}$

6. diagonal matrix 대각행렬은 대각 성분이 0이 아닌 경우 inverse가 존재한다.

   $A = \begin{bmatrix} d_1 & & \\ & \ddots & \\ & & d_n\\ \end{bmatrix} \quad then \quad A^{-1} = \begin{bmatrix} 1/d_1 & & \\ & \ddots & \\ & & 1/d_n\\ \end{bmatrix}$

이렇게 이번 lec 3에서는 행렬의 곱셈에 대한 해석, Inverse matrix, Gauss-Jordan까지 알아보았다. 다음 강의는 LU decomposition에 대해서 알아본다.