#Lec 1. The Geometry of Linear Equations

HoDu PyTHON·2023년 2월 13일

Linear Algebra linear equations 선형대수

선형대수

목록 보기

2/4

🌌 선형대수학에서 배울 것

n개의 식, n개의 미지수로 구성된 linear equation 풀기 : 연립 선형방정식(system of linear equation)을 푸는 것
row picture : 일반적으로 알고 있는 n개의 식, n개의 미지수 → 보통 좌표평면 상 교점으로 해결
column picture : 새로이 배우게될 관점 → vector의 linear combination으로 해결
matrix $A$ 를 통해 linear algebra 관점에서의 문제 해결

간단한 예시를 보자.

\begin{aligned} 2x - y &= 0 \\ -x + 2y &= 3 \end{aligned}

위의 두 수식을 행렬식으로 바꾸는 것을 배울 것이다.

\begin{bmatrix} 2 & -1 \\ -1 & 2 \\ \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} = \begin{bmatrix} 0\\3 \end{bmatrix}

다음과 같이 $Ax = b$ 의 꼴로 바꾸는 것이며, 이때 A는 계수 행렬 (Coefficient Matrix)라고도 한다.
x는 미지수들의 vector이고 b 역시 vector이며 관습적으로 $Ax$ 의 결과를 b라고 부른다.
→ 선형 방정식 (linear equation)은 $Ax=b$ 의 형태이며 이를 푸는 것이 목표

🌌 Row picture & Column picture

✔ Row picture

\begin{aligned} 2x - y &= 0 \\ -x + 2y &= 3 \\ \end{aligned}

Row picture는 두 연립 방정식을 각 식 입장에서 해석하는 문제를 의미한다.

위 두 식에 대해서 row 관점에서 해석하면 아래 그림과 같다.

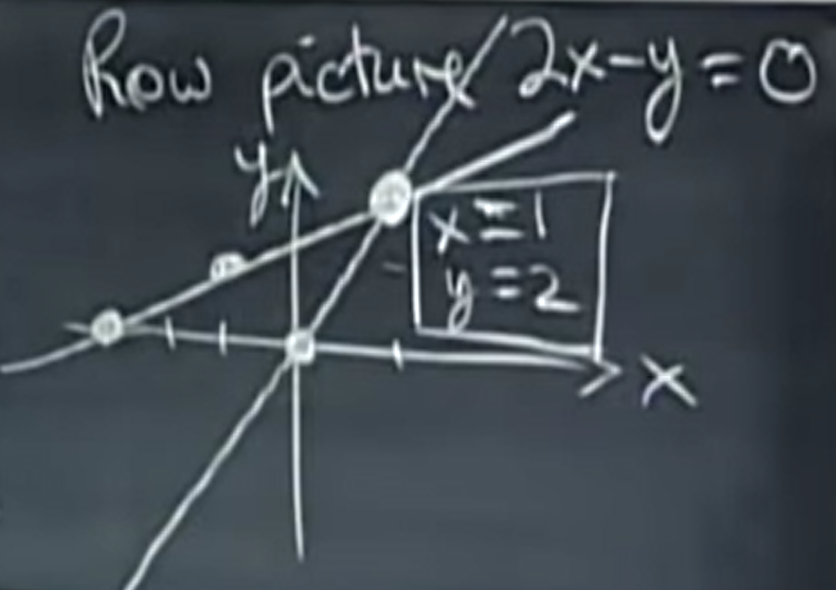
각 식들을 일반적으로 아는 방법으로 두 선분을 그리고 교점을 찾으면 문제를 해결할 수 있다.
이때 x=1, y=2라는 solution(교점)을 가진다.
즉, 한번에 하나의 방정식에 대한 그림

\begin{aligned} 2x - y &= 0 \\ -x + 2y -z &= -1 \\ -3y + 4z &= 4 \end{aligned}

위 처럼 식 3개 미지수 3개에 대한 row picture를 그리면 다음과 같다.

다음과 같이 특별한 경우(평행)가 아니면 3 평면을 ~~(정확하게 그리기는 어렵지만)~~ 한점에서 만난다 (: solution)
하지만 고차원이 될 수록 그리기는 더 어려워지며 시각적으로 확인하는 것은 거의 불가능해진다.

✔ Column picture

x\begin{bmatrix} 2\\-1 \end{bmatrix} + y\begin{bmatrix} -1 \\2 \end{bmatrix} = \begin{bmatrix} 0 \\3 \end{bmatrix}

row picture에서 봤던 식을 위의 식처럼 column vector의 곱과 합 형태로 바꿀수 있으며 이를 linear combination 이라고 한다.

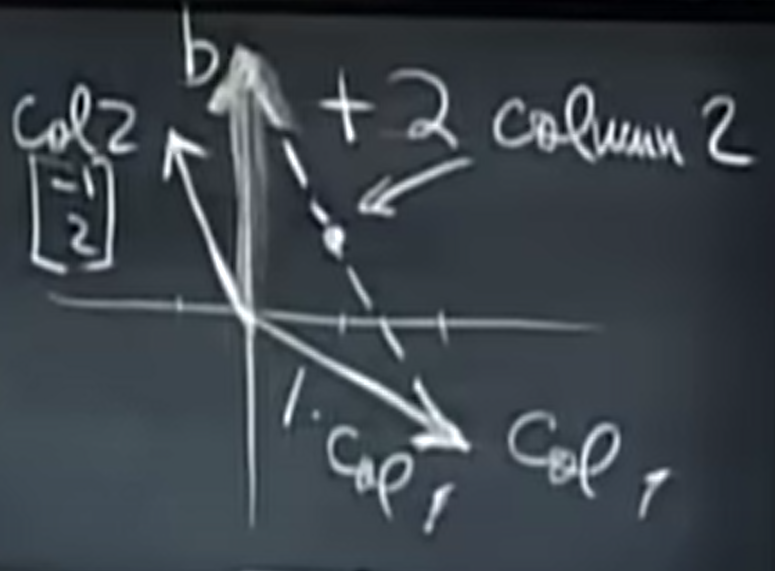이를 vector로 좌표평면 상에 표시하면 다음과 같이 문제를 vector b를 구할 수 있다. (이때 x=1, y=2) + 모든 x,y에 대해서는 평면을 채울 수 있게 된다

즉, 한번에 하나의 column에 대한 그림

x\begin{bmatrix} 2\\-1\\0 \end{bmatrix} + y\begin{bmatrix} -1 \\2\\-3 \end{bmatrix} + z\begin{bmatrix} 0 \\-1 \\4 \end{bmatrix} = \begin{bmatrix} 0 \\-1 \\4 \end{bmatrix}

위의 식처럼 3개의 3차원 vector들의 linear combination으로 표현하고 column picture를 그리면 다음과 같다.

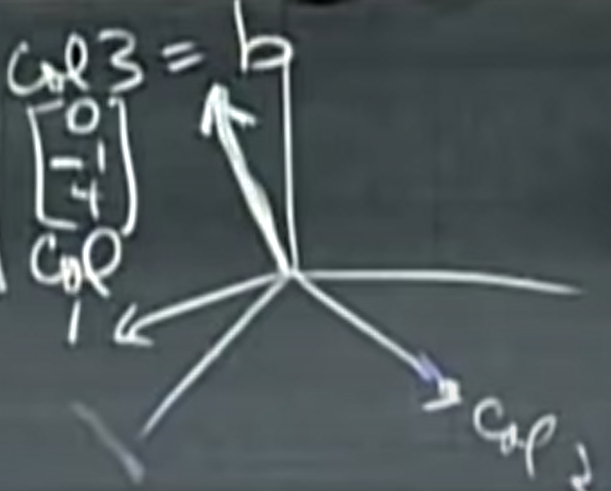solution은 col 3과 같음을 쉽게 알 수 있게 된다. (x=0,y=0,z=1)

위의 3차 연립방정식에 대해 다음과 같은 질문을 할 수 있다.

Can I solve $Ax=b$ for every b?

그리고 위의 질문은 다음과 같이 해석할 수 있다.

→ Do the linear combinations of the columns fill 3-D space?

즉, Ax=b에서 모든 b 대한 해가 존재한다는 것은 3개의 column vectors로 구성된 linear combinations이 3차원 공간을 모두 채운다는 것이다.

위의 case에서 답은 YES 이며 이때 matrix A는 non-singular matrix 이며 invertible matrix라고 한다. (invertible matrix는 역행렬이 존재하는 행렬을 의미)

Elimination (소거) 방법은 solution을 찾기위한 방법을 제공해준다. (lec 2에서)

그렇다면 언제 go wrong할까?
3개의 column vectors이 한 평면위에 놓인다면? (col3가 col1과 col2의 linear combination으로 만들수 있다면) 이때 matrix A는 singular matrix(특이행렬)이자 not invertible matrix이다.

… 아이디어를 확장해서 만약 9차원 벡터가 9개 있다면?

9개의 column vectors이 모두 independent 하다면 1개의 solution이 존재할 수 있다.
하지만 하나의 vector라도 independent하지 못하다면(dependent하면) 9차원 공간을 모두 채울 수 없을 것이다.
가령 9번째 vector가 8번째 vector에 dependent하다면, 9차원 공간 안에 있는 8차원 평면을 채울 것이다. → 해가 존재하지 않는 경우가 있다.

✔ 행렬곱 (Matrix multiplication)

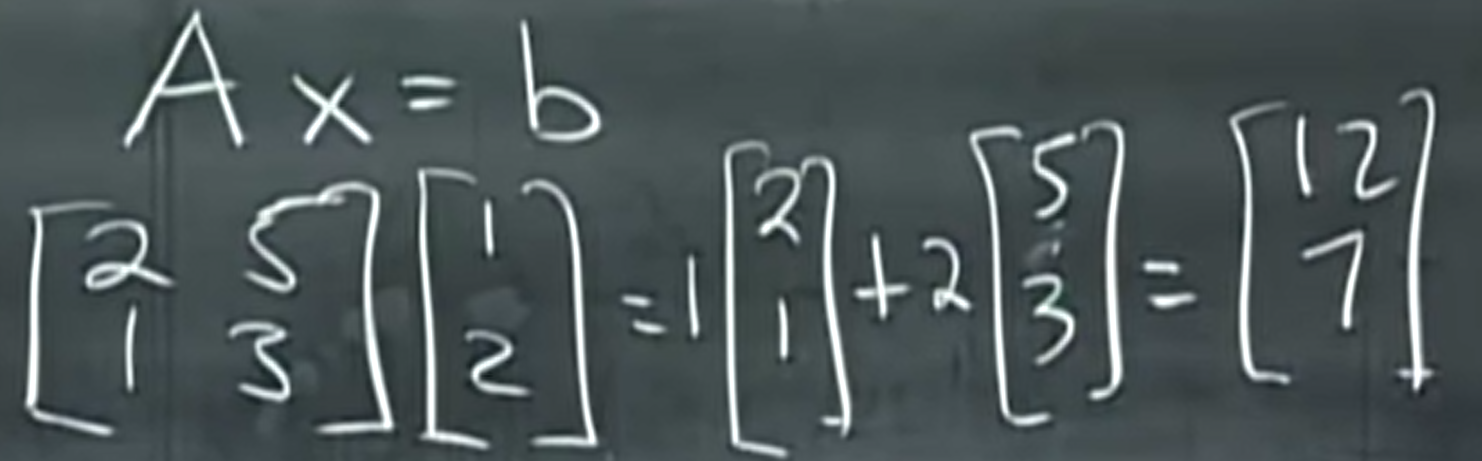
계속 앞에서 봐왔던 수식 $Ax = b$ 는 행렬 A와 벡터 x의 곱이다.
행렬곱은 일반적으로 A의 row와 x의 dot product를 통해 구할 수 있으나 앞선 column picture에서 봤던 form(linear combination 꼴)으로 해석이 가능하다.
더 자세한 내용을 뒤에서 다루기로 하자.

HoDu PyTHON

나는야 척척'박사' & ML/DL & Coffee

이전 포스트

선형대수학 정리노트 #0

다음 포스트