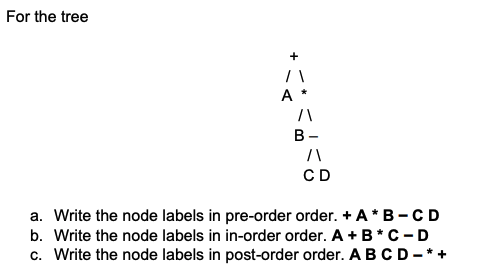
Trees

Problem 4

Write a C++ function TreeNode* copy_tree(TreeNode* T) that returns a copy of binary tree T.

struct TreeNode {
    int m_data;
    TreeNode *m_left;
    TreeNode *m_right;
};


TreeNode* copy_tree(TreeNode* T)
{
   if (T==nullptr) 
        return nullptr;
   return new TreeNode(T->m_data, copy_tree(TreeNode* T->m_left),
   copy_tree(TreeNode* T->m_right));
}

Problem 5

Write a C++ function TreeNode* expand_leaf(TreeNode* node, ItemType x, ItemType y) that returns a new binary tree that is identical to the binary tree T except that every leaf in T now has a left child and a right child whose values are equal to x and y, respectively.

For example, invoking expand_leaf(T, 9, 12) on the tree on the left produces the tree on the right.

TreeNode* expand_leaf(TreeNode* T, ItemType x, ItemType y)
{
   if (T == nullptr) return T;
   
   else {
     if (T->m_left == nullptr && T->m_right == nullptr) {
       T->m_left = new TreeNode(x);
       T->m_right = new TreeNode(y);
     }
     
     if (T->m_left != nullptr)
     	T->m_left = expand_leaf(T->m_left, x, y);
        
     if (T->m_right != nullptr)
     	T->m_right = expand_leaf(T->m_right, x, y);
     return T; // return the (unchanged) pointer T
   }
}

Problem 6

Write a C++ function int height(TreeNode* T) that returns the height of the binary tree T

int height(TreeNode* T) {
    if (T == nullptr) return 0;
    else {
        int lHeight = height(T->m_left);
        int rHeight = height(T->m_right);
        
        if (T->m_left == nullptr && T->m_right == nullptr) {
            if (lHeight > rHeight) return lHeight;
            else return rHeight;
        }
        else {
            if (lHeight > rHeight) return lHeight + 1;
            else return rHeight+1;
        }
    }
}

Problem 7

Write a C++ function bool same_tree(TreeNode* T1, TreeNode* T2) that returns true if binary trees T1 and T2 are exactly the same (same values, same structure) and returns false otherwise.

You may assume that values of ItemType can be compared by means of the == operator.

bool same_tree(TreeNode* T1, TreeNode* T2)
{
    if (T1 == nullptr && T2 == nullptr) return true;
    if (T1 == nullptr || T2 == nullptr) return false;
    return (same_tree(T1->m_left, T2->m_left) 
         && same_tree(T1->m_right, T2->m_right));
}

Problem 8

Write a C++ function TreeNode* bst_insert(ItemType item, TreeNode* T) that inserts item into the binary search tree T. After the insertion, T must remain a binary search tree.

You may assume that ItemType values are comparable using the ==, <, and > C operators.

TreeNode* bst_insert(DataType item, TreeNode* T) {
     if (T == nullptr) {
         T = new TreeNode(item);
         return T;
     }
     else {
         if (item <= T->m_data) 
              T->m_left = bst_insert(item, T->m_left);
         else 
              T->m_right = bst_insert(item, T->m_right);
         return T; // return the (unchanged) pointer T
     }
}

Draw the binary search tree resulting from sequentially calling bst_insert on an initially empty binary tree with the values 9,12,5,15,7,10,18

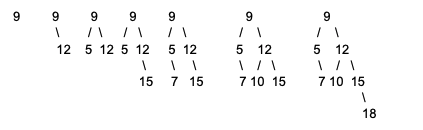
Tree Traversal

Searching

Problem 1

Given an array containing the sequence 1, 5, 29, 45, 67, 76, 92, 104, 187, 234 (in that order)

a. State each comparison made in finding the number 234 using linear search. (For example, 234:1 is a comparison of 234 with 1.)

234:1, 234:5, 234:29, 234:45, 234:67, 234:76, 234:92, 234:104, 234:187, 234:234

b. State each comparison made in determining that the number 48 is not present using linear search.

48:1, 48:5, 48:29, 48:45, 48:67, 48:76, 48:92, 48:104, 48:187, 48:234

Problem 2

a. Given the following sequence of integers (for example, integers received from the keyboard)
29, 234, 1, 45, 92, 76, 67, 187, 104, 5

b. State each comparison made in finding the number 234 using binary search. (For example, 234:1 is a comparison of 234 with 1.)

234:29, 234:234

c. State each comparison made in determining that the number 48 is not present using binary search

48:29, 48:234, 48:45, 48:92, 48:76, 48:67

d. Write the integers as they would be encountered in an in-order traversal of the tree.

(If you use a trick that draws dots under the node along the line starting from 29...)

1, 5, 29, 45, 67, 76, 92, 104, 187, 234

Problem 3

Linear search can be done on data in an array or in a list. Name an advantage and a disadvantage of the list implementation over the array implementation.

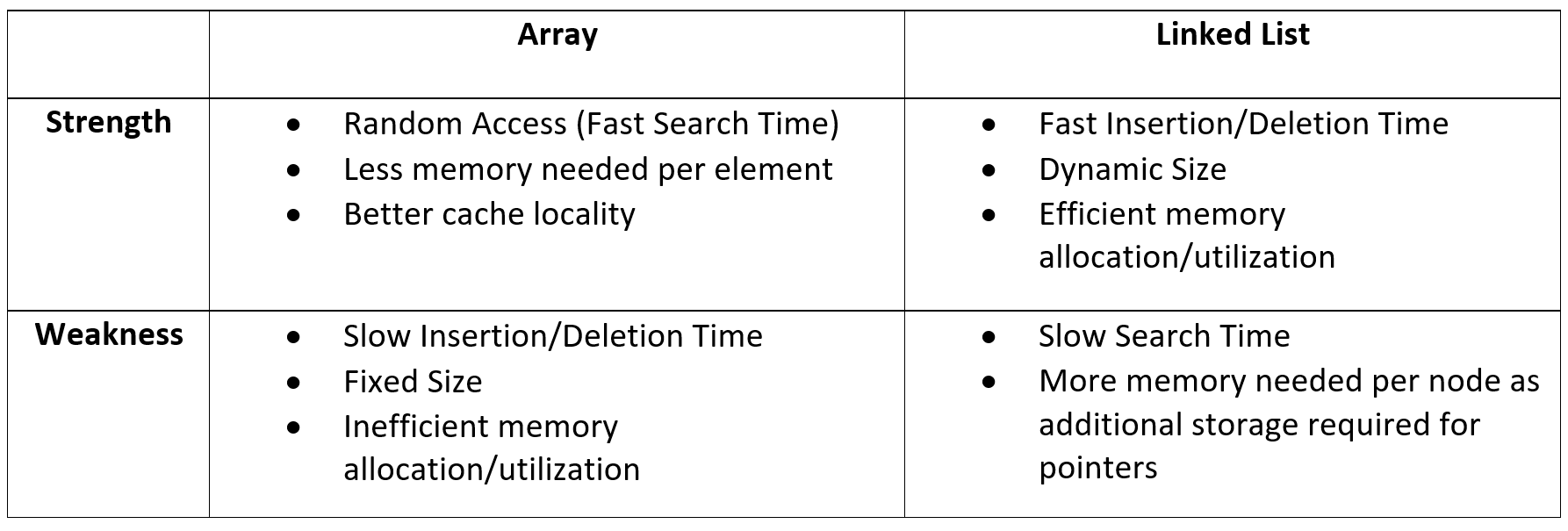
Advantage of list implementation

• No memory restriction

Disadvantage of list implementation

• not as simplistic to implement a list as it is an array

Problem 4

Binary search can be done on data in a sorted array or in a binary search tree. Name an advantage and a disadvantage of the array implementation over the BST implementation.

Advantage of array implementation

• code is easier

Disadvantage of array implementation:

• finite number of items

Sorting

Problem 1

How many permutations of N distinct items are there? N!

Problem 2

Explain why selection sort is O(N2) on average.

Selection sort is O(N2) on average because it takes typically N swap steps with for each of the N items.

Problem 3

Explain why quicksort is O(N log N) on average, but O(N2) worst case.

Quicksort is typically O(N log N) when the data is randomly distributed. However, when the data is mostly or fully sorted, the worst case is O(N2).

Problem 4

Given an array containing the integers 12 9 3 6 4 1 (in that order)

a. Show the array as it is sorted by the selection sort

12 9 3 6 4 1
1 9 3 6 4 12
1 3 9 6 4 12
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12

b. Show the array as it is sorted by the mergesort

12 9 3 6 4 1
12 9 3   6 4 1
12   9 3    6   4 1
12   9   3   6   4   1
12   3 9   6   1 4
3 9 12   1 4 6
1 3 4 6 9 12

c. Show the array as it is sorted by the insertion sort

12 9 3 6 4 1
9 12 3 6 4 1
3 9 12 6 4 1
3 6 9 12 4 1
3 4 6 9 12 1
1 3 4 6 9 12

d. Show the array as it is sorted by the bubble sort

Iteration 1:
12 9 3 6 4 1
9 12 3 6 4 1 (SWAP)
9 3 12 6 4 1 (SWAP)
9 3 6 12 4 1 (SWAP)
9 3 6 4 12 1 (SWAP)
9 3 6 4 1 12 (SWAP)

Iteration 2:
9 3 6 4 1 12
3 9 6 4 1 12 (SWAP)
3 6 9 4 1 12 (SWAP)
3 6 4 9 1 12 (SWAP)
3 6 4 1 9 12 (SWAP)
3 6 4 1 9 12

Iteration 3:
3 6 4 1 9 12
3 6 4 1 9 12
3 4 6 1 9 12 (SWAP)
3 4 1 6 9 12 (SWAP)
3 4 1 6 9 12
3 4 1 6 9 12

Iteration 4:
3 4 1 6 9 12
3 4 1 6 9 12
3 1 4 6 9 12 (SWAP)
3 1 4 6 9 12

3 1 4 6 9 12
3 1 4 6 9 12

Iteration 5:
3 1 4 6 9 12
1 3 4 6 9 12 (SWAP)
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12

Iteration 6:
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12
1 3 4 6 9 12

Problem 5

Write a templated version of both bubble and selection sort.

a. As the numbers of elements to be sorted increases how do the two sorts
compare to one another? They are both O(n2)

Asymptotic Analysis

Put in increasing order based on the following set: O(n3), O(2n), O(n), O(nlog n), O(log n), O(1), O(n2)

O(1), O(log n), O(n), O(n log n), O(n2), O(n3), O(2n)

2. Linear search can be done on data in an array or in a list.

What is the average time complexity for successful search using an array? O(n)
Using a list? O(n)

3. Binary search can be done on data in a sorted array or in a binary search tree.

What is the average time complexity for successful search using the array?
Using the BST? O(log n)

What is the worst case time complexity for each? O(n), which can happen if the data inserted is in fully ascending or descending order

Heap

3. Show a maxheap after inserting each of the following numbers:
   13, 9, 4, 5, 2, 8, 3, 0, 12

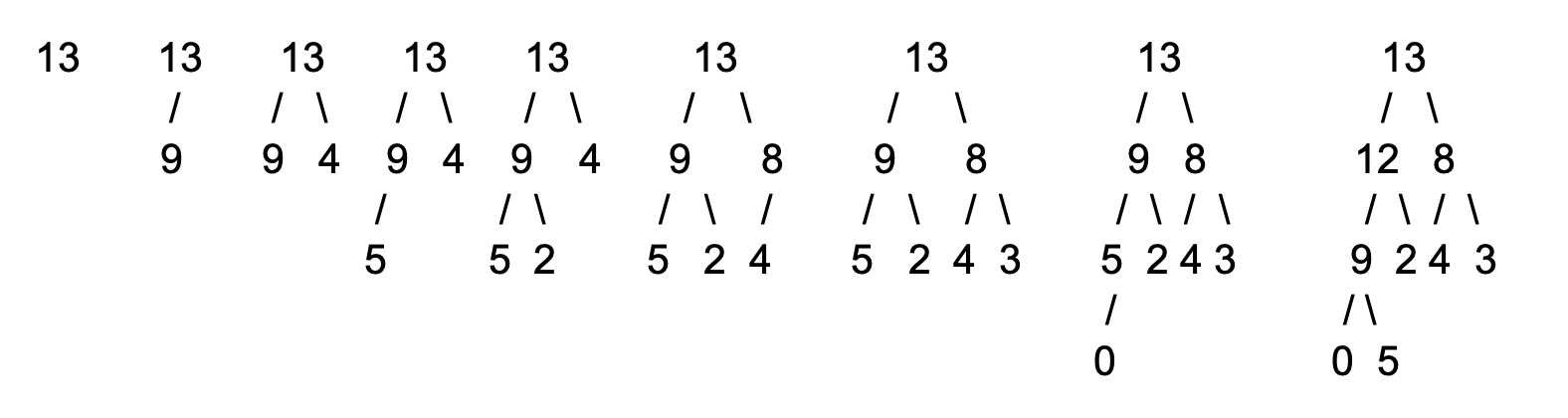
4. Remove the two biggest numbers from the maxheap, showing the heap structure after each deletion.