Quick Sort

Select an arbirary item from the array and set it as P.
Move items smaller than or equal to P to the left and bigger than P to the right.

void QuickSort(int Arr[], int First, int Last)
{ 
   if (Last-First >= 1) {
   	int pivotIndex;
    
    pivotIndex = Partition(Arr, First, Last);
    QuickSort(Arr, First, pivotIndex-1);
    QuickSort(Arr, pivotIndex+1, Last);
   }
}

int Partition(int a[], int low, int high)
{
   int pi = low;
   int pivot = a[low];
   
   do 
   {
    	while (low <= high && a[low] <= pivot)
    		low++;
    	while (a[high] > pivot)
    		high-- ; 
    	if (low < high)
    		swap(a[low], a[high]);
   } while (low < high);
   
   swap(a[pi], a[high]);
   pi = high;
   return pi;
}

Big-O Analysis: nlog_2(n)

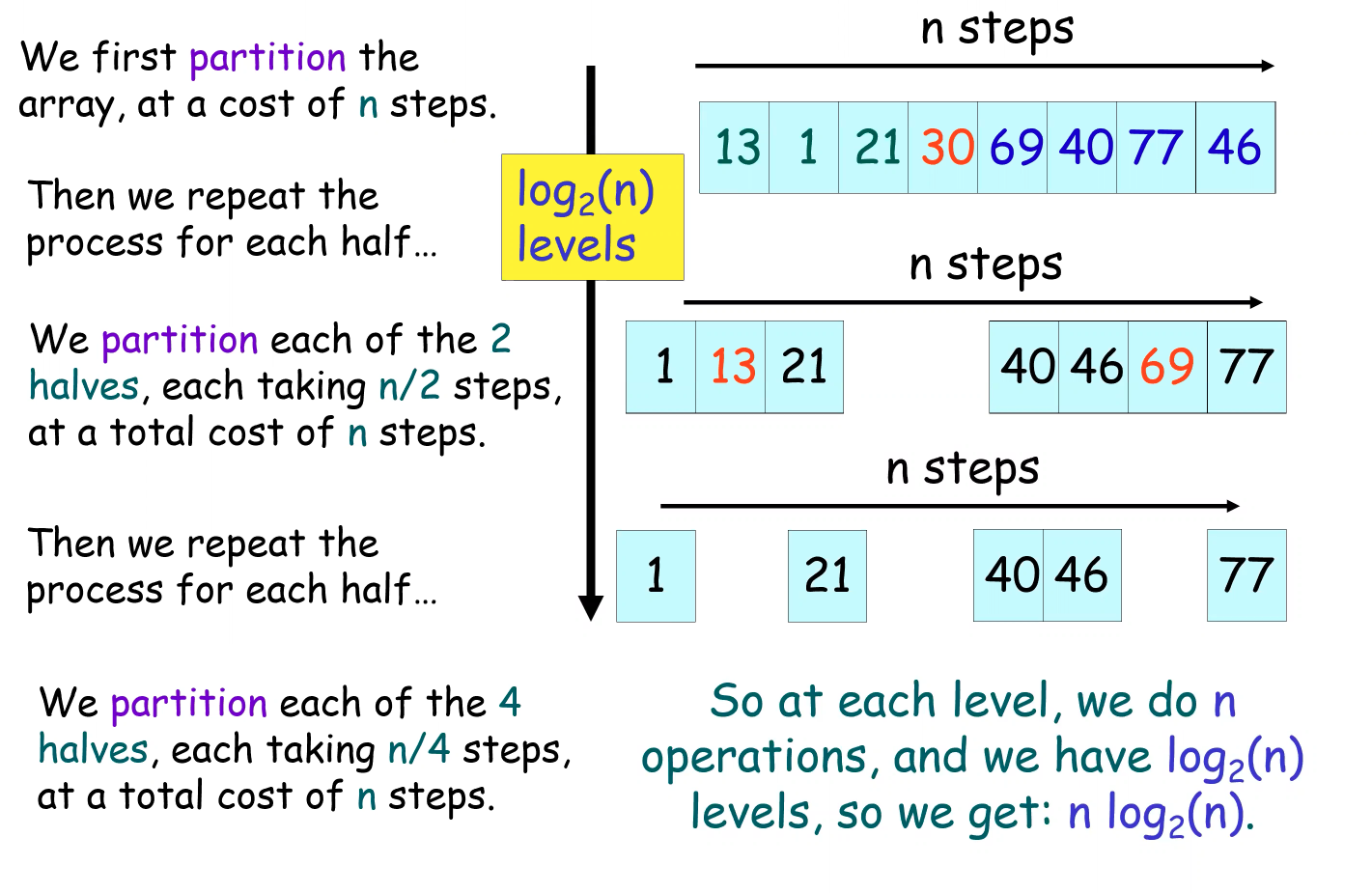
Big-O Worst Case Scenario: n^2

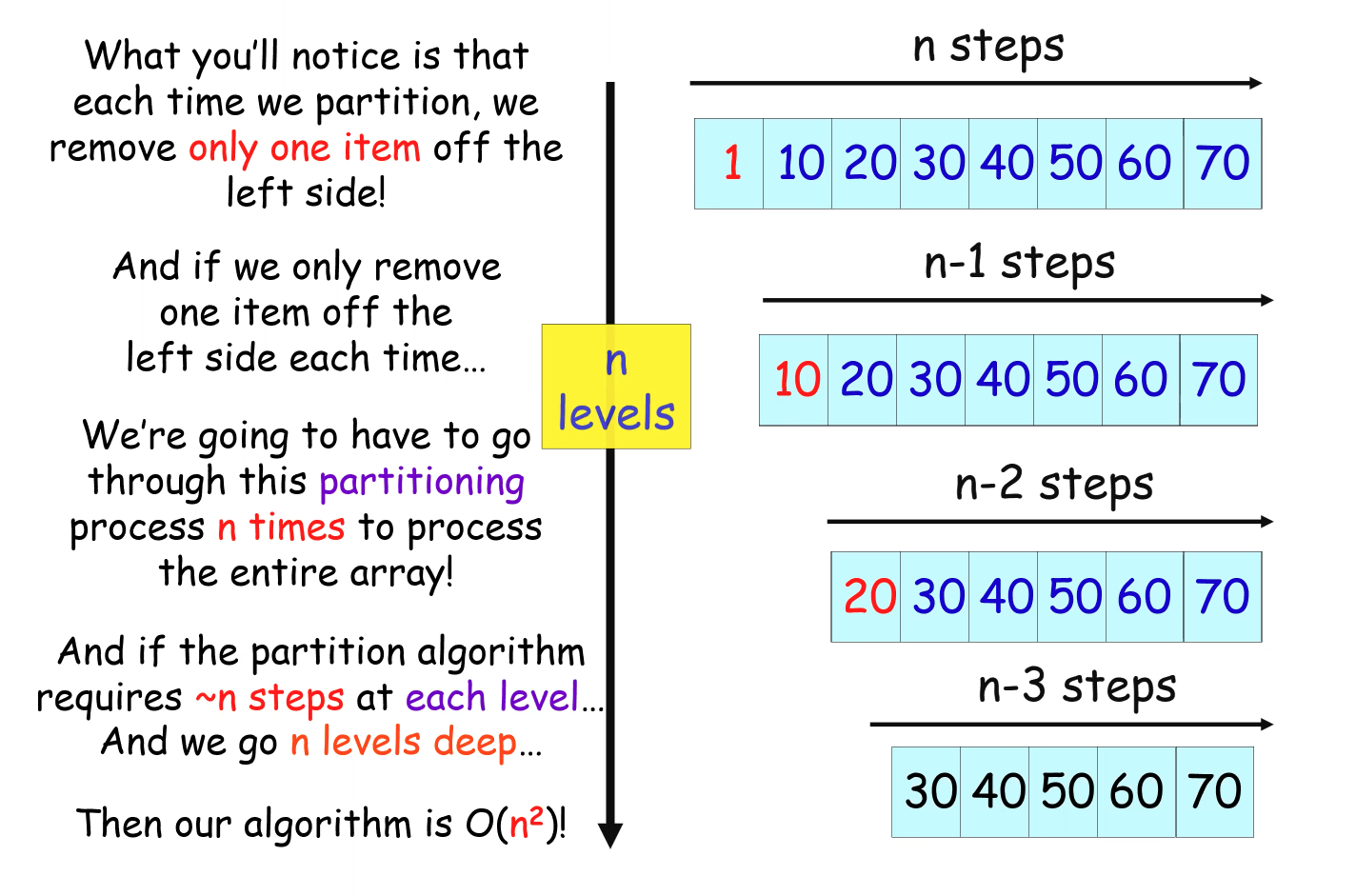
If the items are mostly sorted, or have to do it in a reverse order, avoid quick sort!

Questions

1. Can it be applies easily to sort items within a linked list? Yes
2. Is quick sort a "stable" sort? No
3. Does quick sort use a fixed amount of RAM, or can it vary? Fixed.
4. Can it be parallelized across multiple cores? Yes
5. When might you use quick sort?

Merge Sort

The basic merge algorithm takes two-presorted arrays as inputs and outputs a combined, third sorted array.

void merge(int data[], int n1, int n2)
{
   int i=0, j=0, k=0;
   int *temp = new int[n1+n2];
   int *sechalf = data + n1;
   
   while (i<n1 || j<n2)
   {
      if (i==n1)
         temp[k++] = sechalf[j++];
      else if (j==n2)
         temp[k++] = data[i++];
      else if (data[i] <= sechalf[j])
         temp[k++] = data[i++];
      else 
         temp[k++] = sechalf[j++];
   }
   
   for (i=0; i<n1+n2; i++)
      data[i] = temp[i];
   delete[] temp;
}

Instead of passing in A1, A2, and B, you pass in an array called data and two sizes: n1 and n2.

The function also uses new/delete to allocate temporary array for merging.

Big-O Analysis: n*log_2(n)

There is not really worst case scenario for merge sort

Questions

1. Can merge sort be applied easily to sort items within a linked list? Yes
2. "stable"? Yes
3. Can it be parallelized across multiple cores? Yes

Summary

Trees

• To organize hierarchial data
• To make information easily searchable
• To simplify the evaluation of mathematical expressions
• To make decisions

Binary Tree

In a binary tree, every node has at most two children nodes.

Traversal

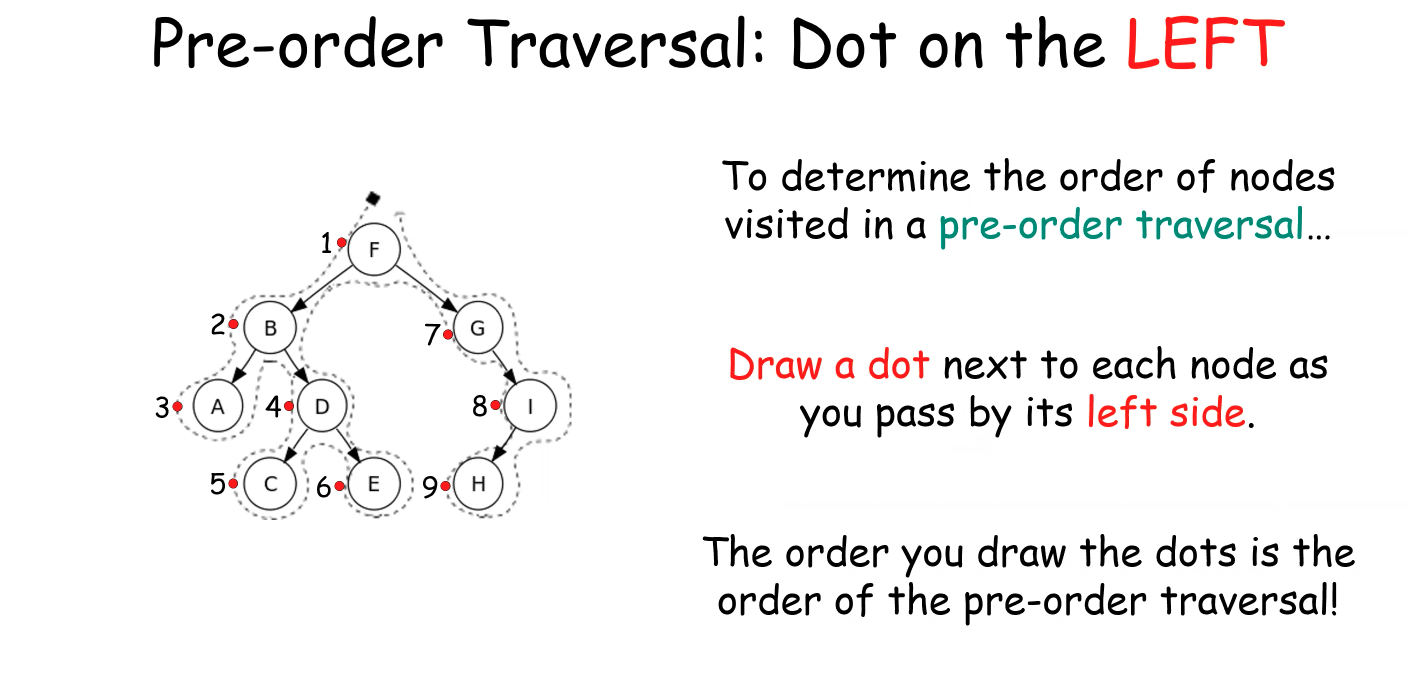
Pre-order Traversal

1. Process the current node.
2. Recursively call PreOrder on the left sub-tree.
3. Recursively call PreOrder on the right sub-tree.

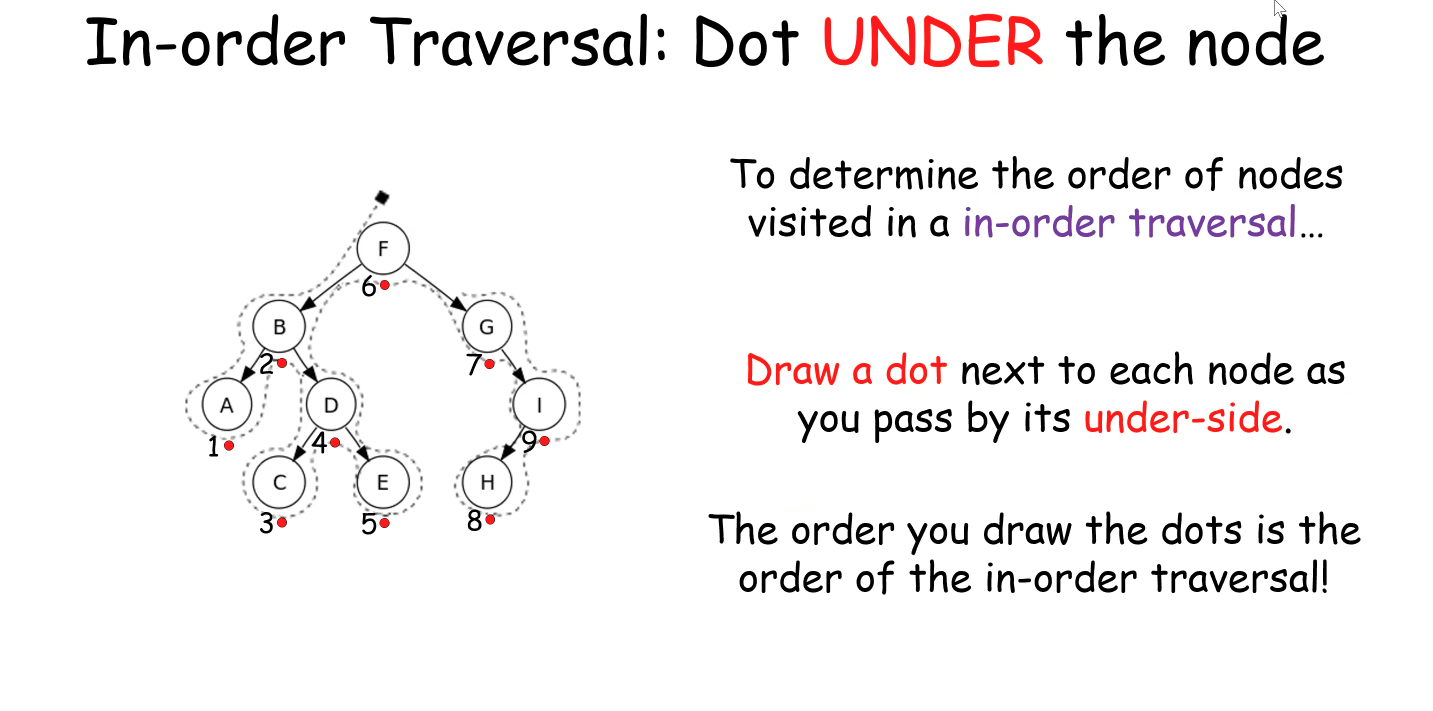
In-order Traversal

1. Process the nodes in the left sub-tree
2. Process the current node
3. Process the nodes in the right sub-tree

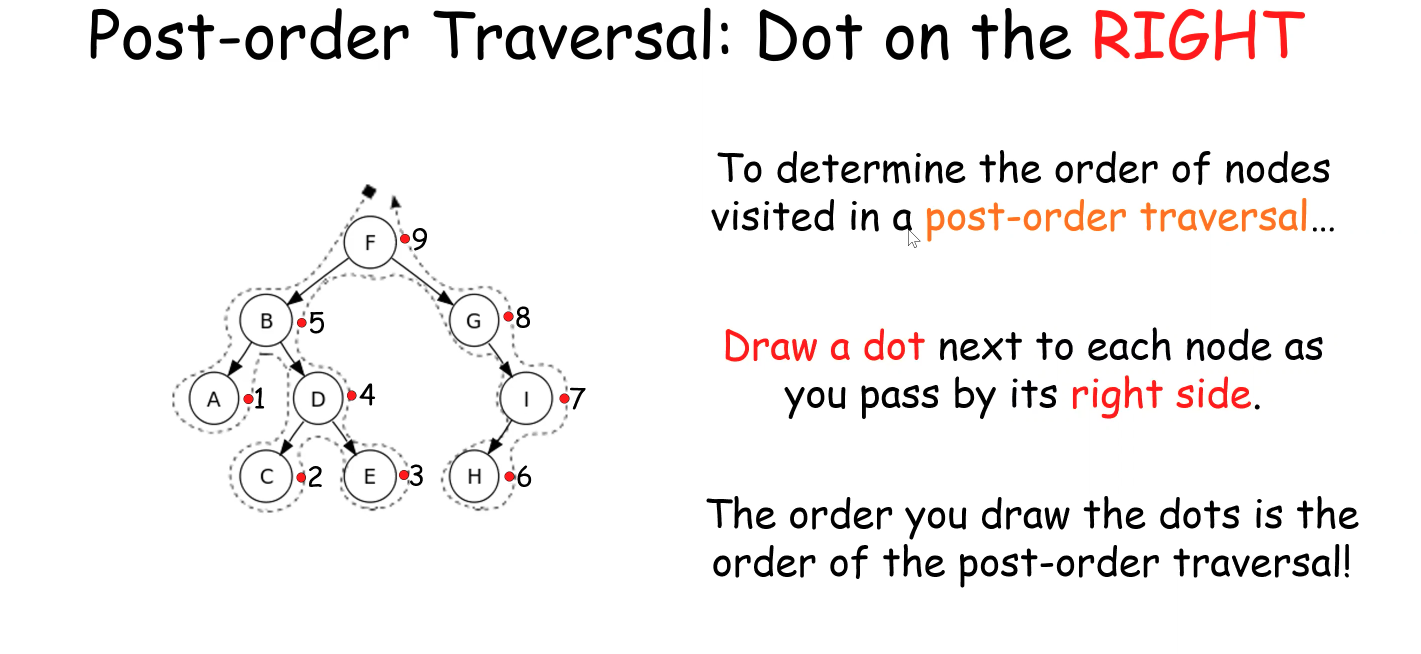
Post-order Traversal

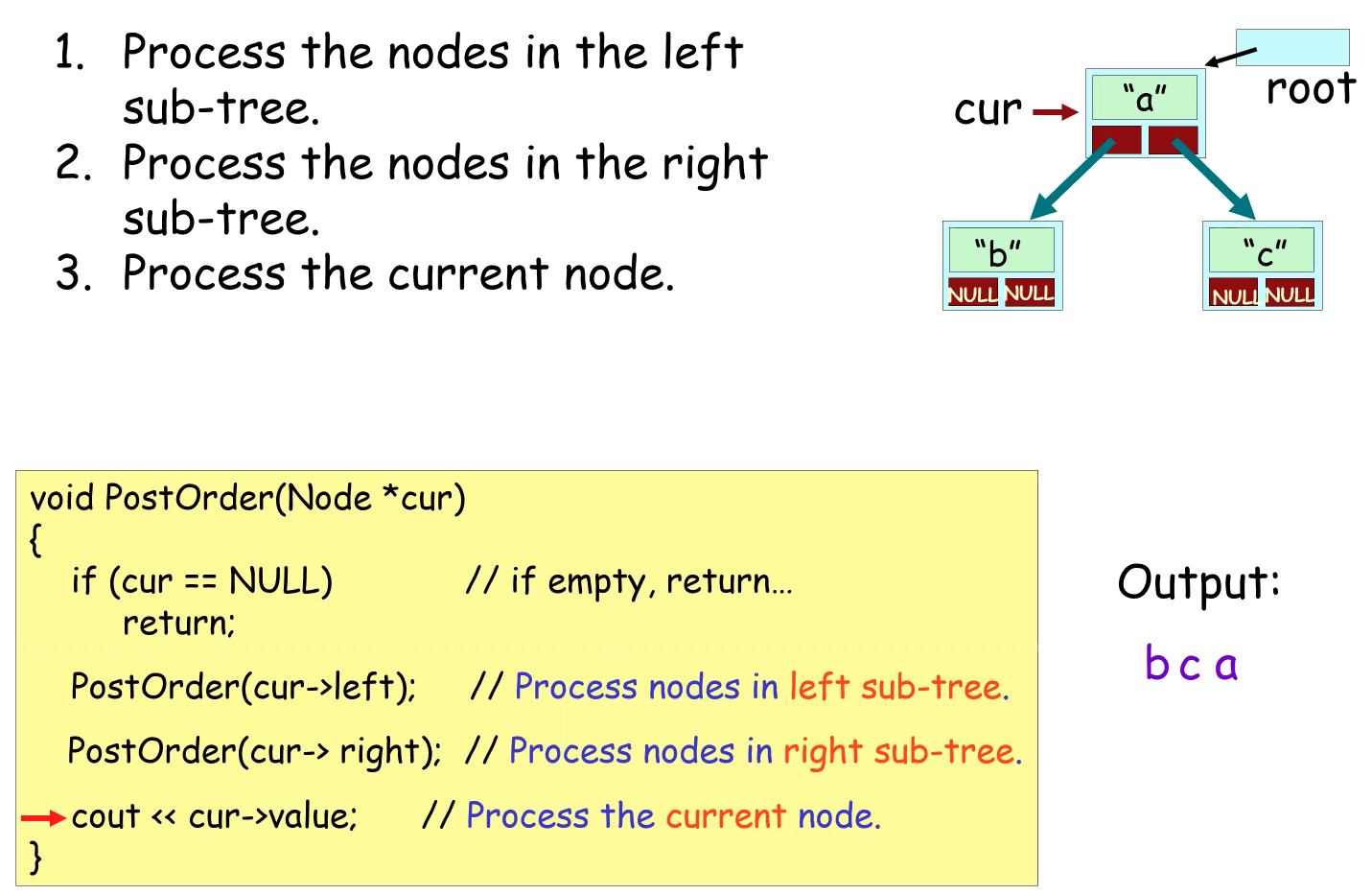
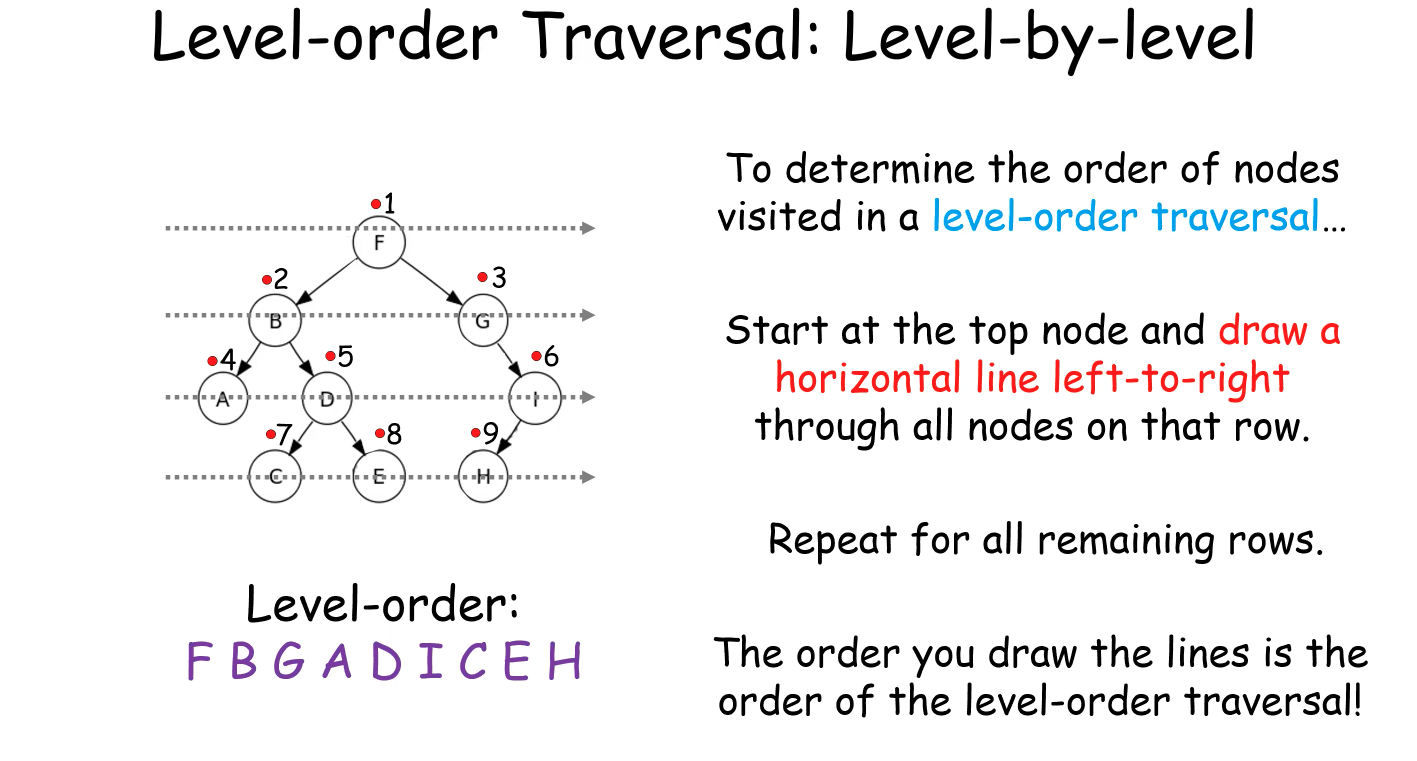
Level-order Traversal

Big-O for traversal: O(n)

N nodes in a tree. As a traversal must visit each node in the tree, no matter what traversal is, O(n).

Class Challenge

1. In-order?

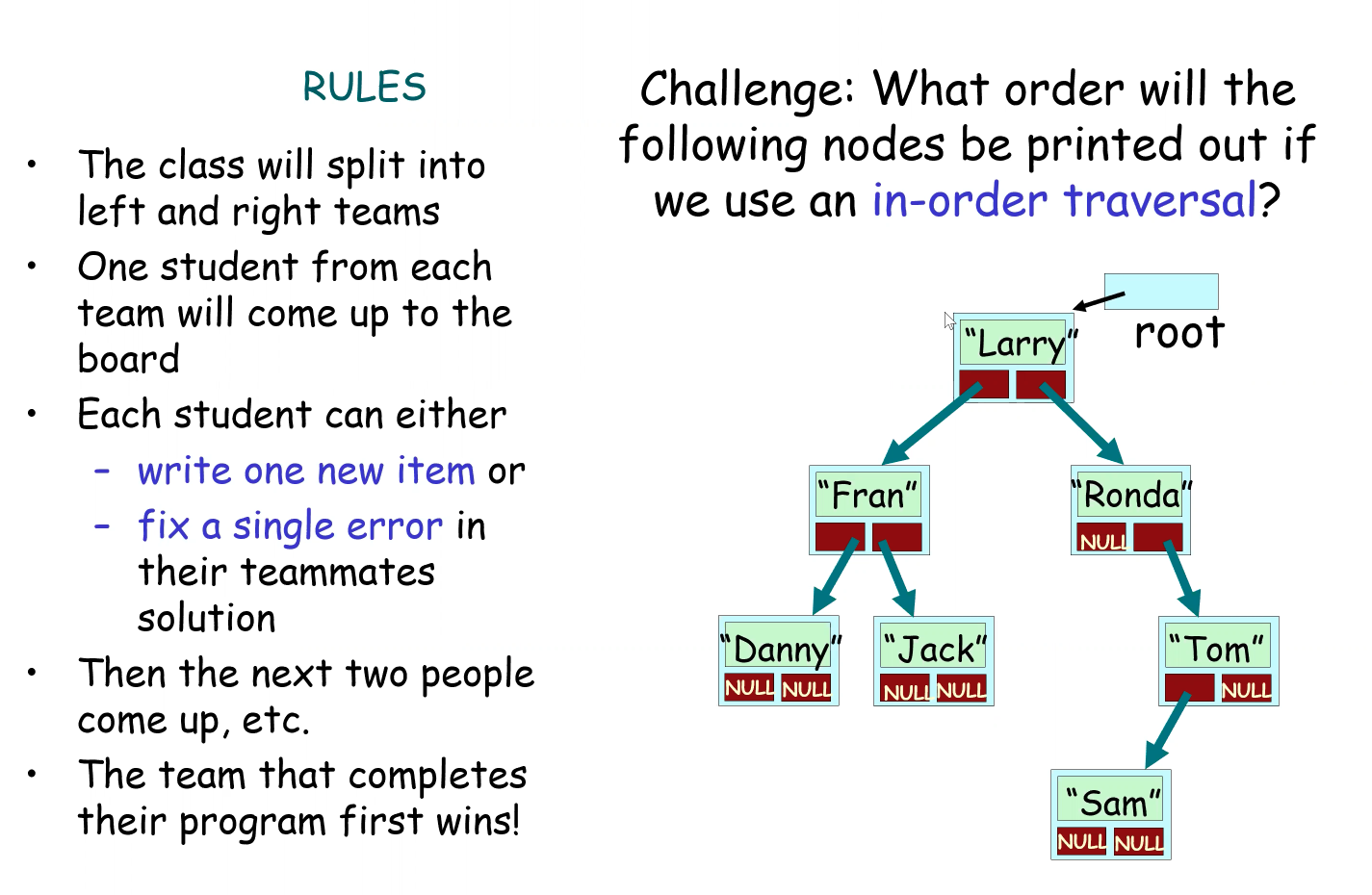
Start from far-left:
Danny-Fran-Jack-Larry-Ronda-Sam-Tom

Handy Tricks (Draw Lines and Dots)

선과 점을 그리는 것으로부터 각 Traversal이 어떤 순서로 진행될지 예측할 수 있다.