Heap

Priority Queue

Priority queue: queue that allows us to keep a prioritized list of items

Operations:

• Insert a new item into the queue
• Get the value of the highest priority item
• Remove the highest priority item from the queue

For a limited number of set of priorities, we can use a linked list.

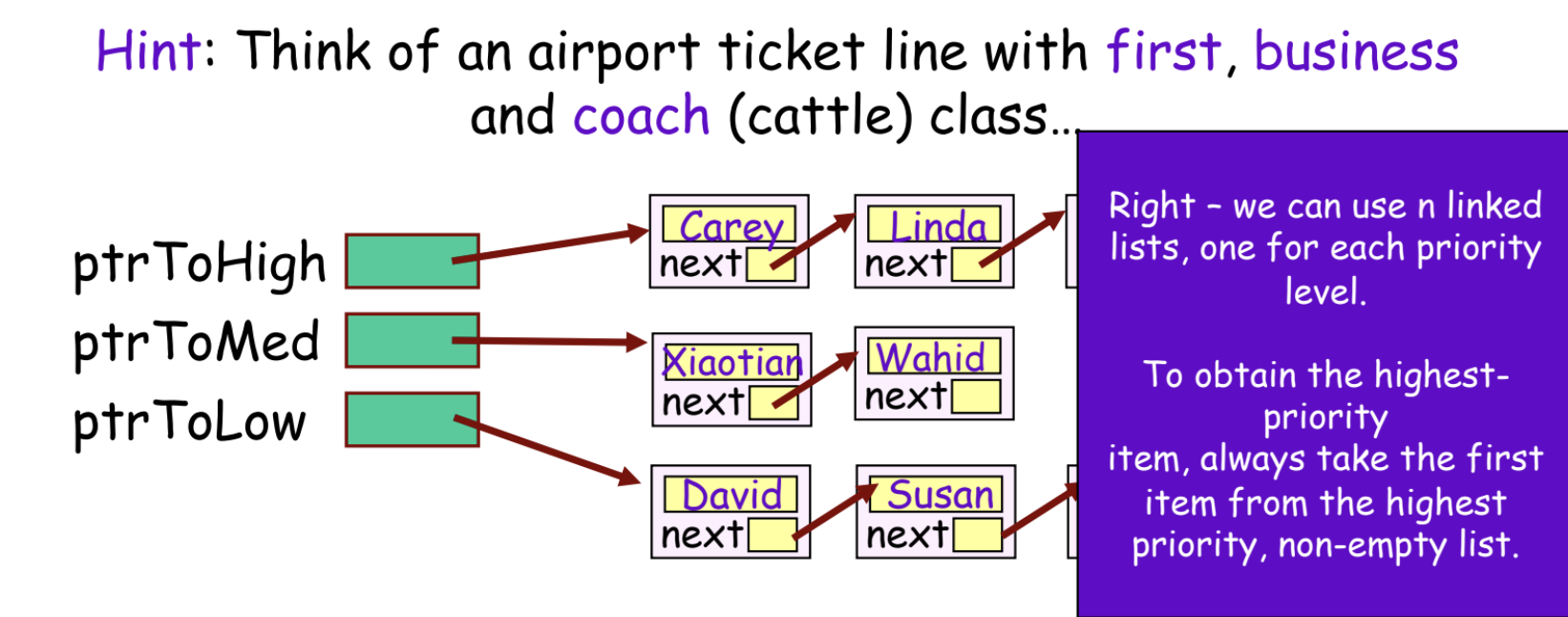
For a huge number of priorities, the heap data structure is one of the most efficient ones we can use to implement a priority queue.

complete binary tree

All heaps use a "complete binary tree".

complete binary tree

• The top n-1 levels of the tree are completely filled with nodes
• All nodes on the bottom-most level must be as far left as possible

---

Maxheap

1. The value contained by a node is always greater than or equal to the values of the node's children.
2. The tree is a complete binary tree.

Extraction

How to take 12 out of the heap?

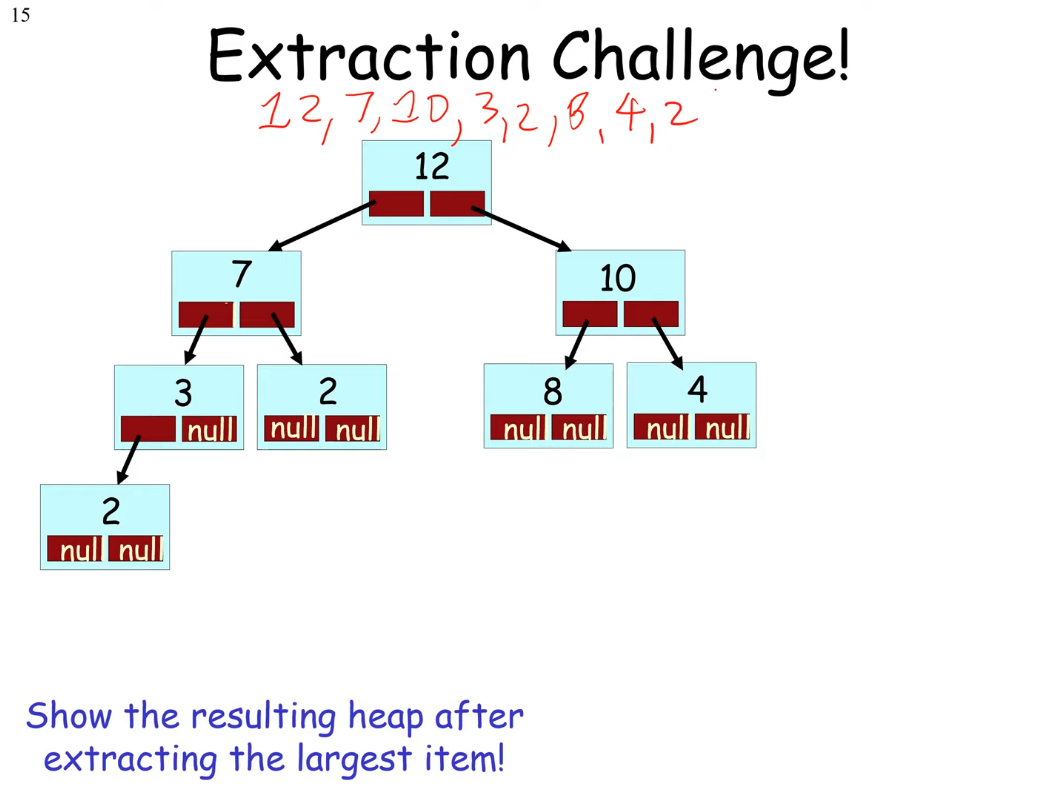
Process:
1. 12 is extracted
2. 2 (bottom-left) goes to where 12 was
3. Pick 10 (10 > 7) and swap 2 and 10.
4. Swap 2 and 8.


Result:
        10
      /    \
    7        8
  /   \    /   \
 3     2  2     4 
  
  
10, 7, 8, 3, 2, 2, 4

Insertion

This process is called "reheapification".

How to insert 9?

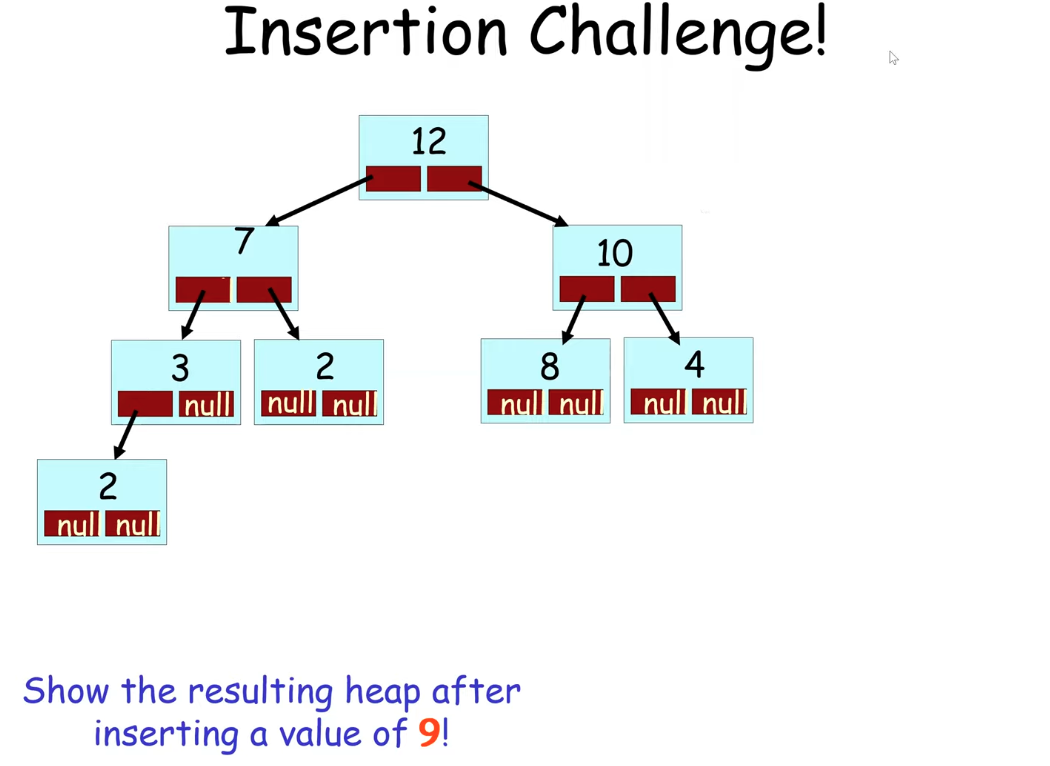
Result:
             12
           /    \
          9      10
        /  \    /  \
       7    2  8    4
     /  \
    2    3
      
Result: 12, 9, 10, 7, 2, 8, 4, 2, 3

Array-based Maxheap

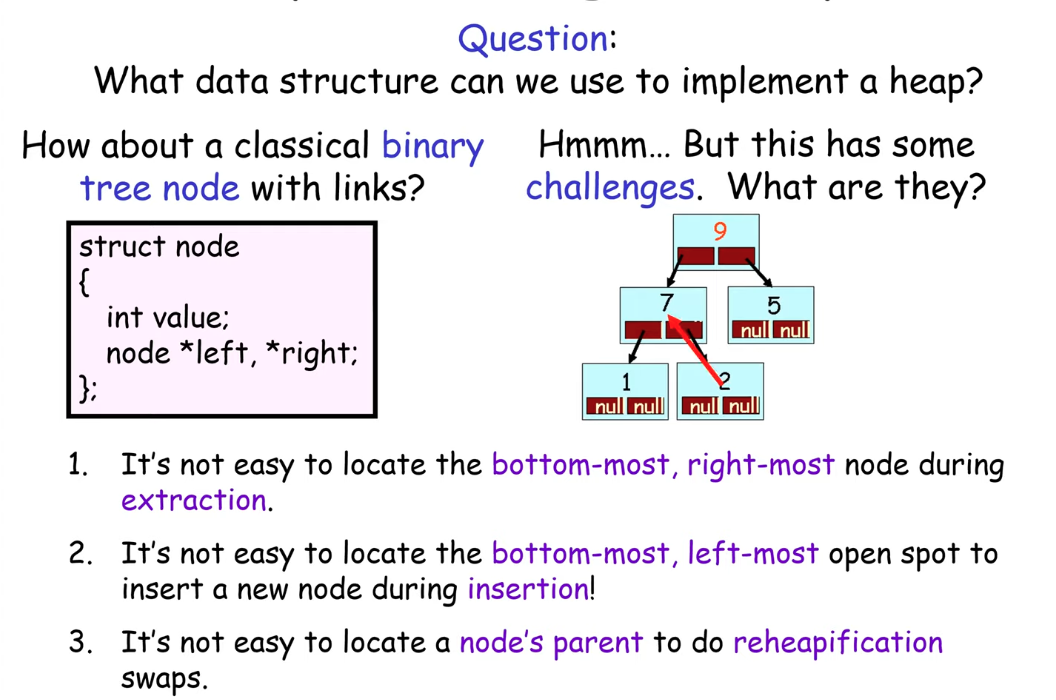
Then, rather than with a classical binary tree node, how about implementing a heap with an array??

With some formula, an array-based heap allows us to

• locate the root node of the tree
• locate and delete the bottom-right, right-most node in the tree
• add a new node in the bottom-most, left-most empty position in the tree
• easily locate the parent and children of any node in the tree

Big-O Analysis: log_2(n)

---

Heapsort

Summary of algorithm

1. Convert your randomly-arranged input array into a maxheap by shuffling around the values.

2. While there are numbers left in the heap:
   A. Remove the biggest value from the heap
   B. Place it in the last open slot of the array