[알고리즘] 깊이 우선 탐색(DFS)

깊이 우선 탐색(DFS, Depth-First Search)

깊이 우선 탐색(DFS) 이란

루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

• 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로 부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
• 즉, 넓게(wide)탐색하기 전에, 깊게(deep) 탐색하는 것이다.
• 사용하는 경우 : 모든 노드를 방문하고자 하는 경우에 이 방법을 선택한다.
• 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
• 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.

깊이 우선 탐색(DFS)의 특징

• 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다
• 전위 순회(Pre-Order Traversalas)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
• 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
  - 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
  

깊이 우선 탐색(DFS)의 과정

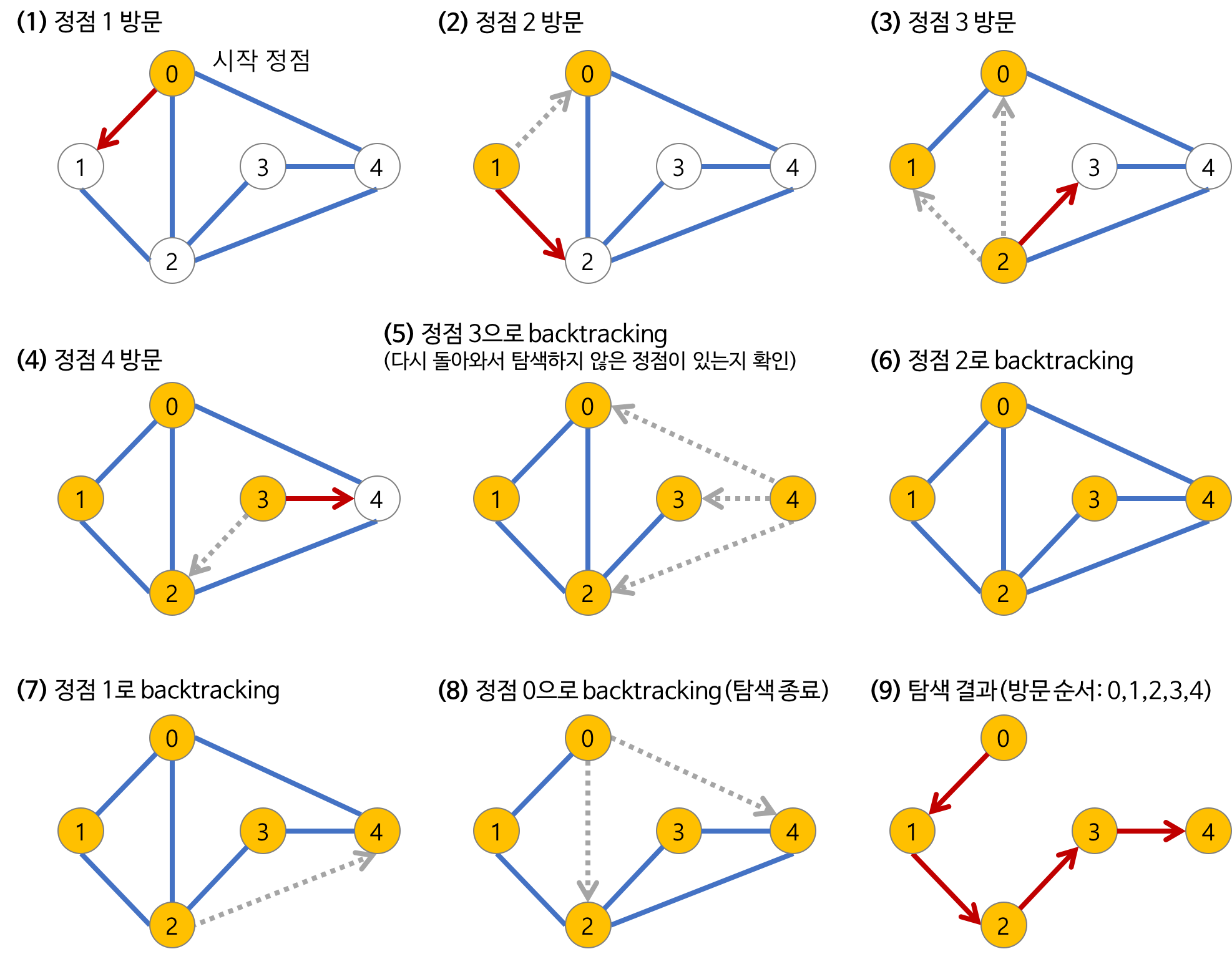
1. a노드(시작 노드)를 방문한다

• 방문한 노드는 방문했다고 표시한다.

2. a와 인접한 노드들을 차례로 순회한다.

• a와 인접한 노드가 없다면 종료한다.

3. a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.

• b를 시작 정점으로 DFS를 다시 시작하게 하여 b의 이웃 노드들을 방문한다.

4. b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.

• 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃노드들을 방문할 수 있다는 뜻이다.
• 아직 방문이 안 된 정점이 없으면 종료한다.
• 있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.

깊이 우선 탐색(DFS)의 구현

• 구현방법 2가지
  - 1. 순환 호출 이용 (재귀함수)
  • 2. 명시적인 스택 이용
    • 명시적인 스택을 사용하여 방문한 정점들을 스택에 저장하였다가 다시 꺼내어 작업한다.

Recursion 이용

#include <iostream>
#include <stdio.h>
#include <vector>
#include <algorithm>
#define MAXV 5
using namespace std;

int visit[MAXV] = { 0 };
vector<int> adj[MAXV];

void dfs_recursion(int start) {
	if (visit[start]) { //방문한 경우 바로 빠져나옴
		return;
	}
	
	visit[start] = true; //방문한 노드 표시
	printf("%d ", start);

	//인접한 노드들 방문
	for (int i = 0; i < adj[start].size(); i++) {
		int x = adj[start][i];
		dfs_recursion(x);
	}
}

stack 이용

#include <iostream>
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <stack>
#define MAXV 5
using namespace std;

int visit[MAXV] = { 0 };
vector<int> adj[MAXV];

void dfs_recursion(int start) {

	if (visit[start]) return;

	stack<int> s;
	s.push(start);
	visit[start] = 1;
	printf("%d ", start);

	while (!s.empty()) {
		int here = s.top();
		s.pop();
		for (int i = 0; i < adj[here].size(); i++) {
			int next = adj[here][i];
			if (visit[next] == 0) {
				printf("%d ", next);
				visit[next] = 1;
				s.push(here);
				s.push(next);
				break;
			}
		}
	}
	
}

main

int main() {
	adj[0].push_back(1);
	adj[1].push_back(0);
	adj[0].push_back(2);
	adj[2].push_back(0);
	adj[0].push_back(4);
	adj[4].push_back(0);

	adj[1].push_back(2);
	adj[2].push_back(1);

	adj[2].push_back(3);
	adj[3].push_back(2);
	adj[2].push_back(4);
	adj[4].push_back(2);

	adj[3].push_back(4);
	adj[4].push_back(3);

	dfs_recursion(0);

	return 0;
}

깊이 우선 탐색(DFS)의 시간 복잡도

• DFS의 그래프(정점의 수:N, 간선의 수:E)의 모든 간선을 조회한다.
  * 인접리스트로 표현된 그래프 : O(N+E)
  • 인접 행렬로 표현된 그래프 : O(N^2)
• 즉, 그래프 내에 적은 숫자의 간선만을 가지는 희소그래프의 경우 인접 행렬 보다 인접 리스트를 사용하는 것이 유리하다.