이진탐색트리?
이진탐색트리란 이진탐색(binary search)와 연결리스트(linked list)를 결합한 자료구조의 일종이다.
이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게 끔 고안되었다.
이진탐색의 경우, 탐색에 소요되는 계산 복잡성은 O(log n)으로 빠르지만 자료 입력, 삭제가 불가능하다. 연결리스트의 경우 자료 입력, 삭제에 필요한 계산 복잡성은 O(1)로 효율적이지만 탐색하는 데에는 O(n)의 계산 복잡성이 발생한다. 두마리 토끼를 잡아보자는 것이 이진탐색 트리의 목적이다.
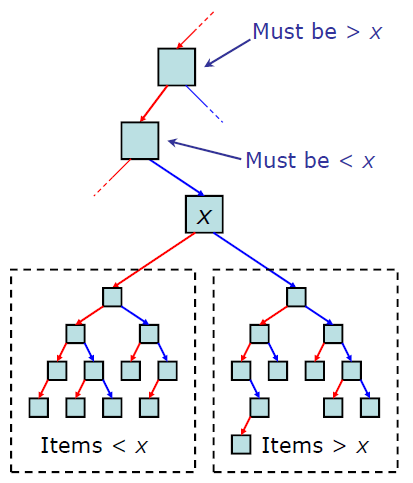
<이진탐색트리의 특징>
* 각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있다.
* 각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있다.
* 중복된 노드가 없어야 한다.
* 왼쪽 서브트리, 오른쪽 서브트리 또한 이진 탐색 트리이다.이진탐색트리를 순회할 때는 중위순회(inorder)방식을 쓴다. 이렇게 하면 이진탐색트리 내에 있는 모든 값들을 정렬된 순서대로 읽을 수 있다.
검색, 삽입, 삭제
이진탐색트리의 핵심 연산은 검색, 삽입, 삭제 세가지 이다.
이 밖에 이진탐색트리 생성 삭제, 비어있는지 확인, 순회 등 연산이 있다.
typedef struct node{
int key;
struct node* left;
struct node* right;
}NODE;
NODE* init_node(NODE * node, int data){
node->key=data;
node->left=NULL;
node->right=NULL;
return node;
}
탐색
아래 이진탐색트리에서 10을 탐색한다고 가정하자. 이진탐색트리는 부모노드가 왼쪽 자식노드보다 크거나 같고, 오른쪽 자식노드 보다 작거나 같다는 점에 착안하면 효율적인 탐색이 가능하다.
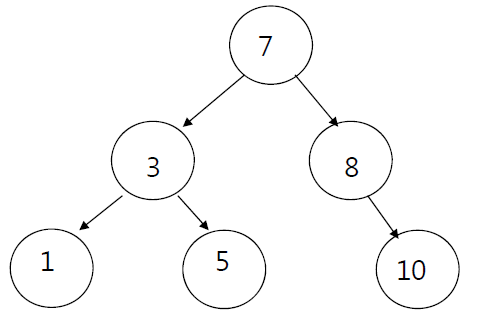
우선 루트노드(7)과 10을 비교한다. 10은 7보다 크므로 따라서 왼쪽 서브트리(1,3,5)는 고려할 필요가 없다. 탐색 공간이 대폭 줄어든다는 말이다.
이번엔 오른쪽 서브트리의 루트노드(8)과 10을 비교한다. 10은 8보다 크다. 따라서 오른쪽 서브트리의 루트노드(10)과 10을 비교한다. 원하는 값을 찾았다.
요컨대 10을 탐색할때 비교하는 값은 다음과 같다.
7,8,10
이번엔 4를 탐색해보자. 위와 같은 방식으로 4를 탐색할 때는 비교하는 값은 다음과 같다.
7,3,5
하지만 5까지 비교했는 데도 원하는 값(4)를 찾지 못했다. 그 다음은 5의 왼쪽 서브트리를 비교할 차례인데 5는 리프 노드여서 서브트리가 존재하지 않는다. 이 경우 '값을 찾지 못했다'고 반환하고 탐색을 종료한다.
이진탐색트리의 탐색 연산에 소요되는 시간복잡도는 트리의 높이가 h일때 O(h)가 된다. 최악의 경우 리프노드까지 탐색해야 하기 떄문이다. 이때 h번이 비교 연산을 수행한다.
<recursive version>
NODE *search1(NODE *node, int key){
//찾고자 하는 값을 찾아봤는데 아예 없었을 경우 혹은 애초에 node 자체가 null이였을 경우
if(!node)
return NULL;
//순환으로 탐색 중 원한느 값을 찾았을 때
if(key == node->val)
return node;
//찾는 값보다 루트 키 값이 작은 경우 오른쪽 서브트리로 이동
else if(key > node->val)
search1(node->right, key);
//찾는 값보다 루트 키 값이 큰 경우 왼쪽 서브트리로 이동
else
search1(node->left, key);
}
<iterative version>
NODE *search2(NODE *node, int key){
/*찾고자 하는 값을 찾아봤는데 아예 없었을 경우
혹은 애초에 node 자체가 null 이었을 경우 whild 문을 탈출하게 된다*/
while(node) //node가 NULL이 아니라면 일단 탐색을 계속 한다.
{
//원하는 키 값을 발견했을 경우
if(key == node->key)
return node; //해당 노드의 주소 반환
//찾고자 하는 값보다 루트키 값이 더 큰 경우 왼쪽 서브트리로 이동
else if(key < node->key)
node = node->left;
//찾고자 한느 값보다 루트키 값이 더 작은 경우 오른쪽 서브트리로 이동
else
node = node->right;
}
return NULL;
}매개변수로 넘어온 NODE *node의 경우 원본의 복사본이므로, 변경하여도 원본에 영향이 가지는 않는다. 물론 node->val 값을 건드리는 것은 절대 안된다. 그렇게 하면 원본에 영향이 가는 것 이기 떄문이다. 여기서 변경해도 된다고 한건 node가 가지고 있는 주소값 자체다. 애초에 탐색 알고리즘은 값을 쓰는게 아니라 읽고 비교만 하는 것 이기 떄문에 node->key 값을 변경하는 일은 없을테지만 말이다.
삽입
이번에는 삽입연산이다. 새로운 데이터는 트리의 리프노드에 붙인다. 예를들어 탐색 예시에 제시한 트리에 4를 추가한다고 가정해보자. 아래와 같다
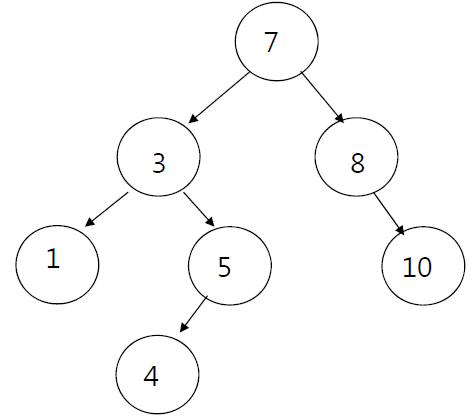
그런데 위 트리에서 7과 3 사이에 트리를 추가해도 이진트리의 속성이 깨지지 않음을 확인할 수 있다. 하지만 이진탐색트리가 커질 경우 이렇게 트리의 중간에 새 데이터를 삽입하게 되면 서브트리의 속성이 깨질 수 있기 떄문에 삽입 연산은 반드시 잎새노드에서 이뤄지게 된다.
이진탐색트리의 가장 왼쪽 잎새노드는 해당 트리의 최소값, 제일 오른쪽 잎새노드는 최대값이 된다.
이진탐색트리의 삽입 연산에 소요되는 시간복잡도는 트리의 높이가 h일때 O(h)가 된다. 삽입할 위치의 잎새노드까지 찾아내려가는데 h번 비교를 해야하기 때문이다. 물론 탐색연산과 비교해 삽입이라는 계산이 추가되긴 하나 연결리스트 삽입의 계산복잡성은 O(1)이므로 무시할 만한 수준이다.
덧붙여 삽입하려는 데이터가 이미 존재하는 것 일수도 있기 때문에 먼저 탐색을 해야만 한다. 결과적으로 탐색을 실패한 위치가 바로 새로운 노드를 삽입하는 위치가 된다.
위에서 4를 삽입하기 위해 먼저 4가 있나 탐색을 시작한다. 루트키인 7보다 4가 더 작으므로 왼쪽 서브트리로 이동한다. 새로운 루트키인 3보다는 크므로 오른쪽 서브트리로 이동한다. 새로운 루트키인 5보다는 4가 작으므로 왼쪽 서브트리로 이동한다. 왼쪽 서브트리는 NULL이므로 탐색이 끝난다.
void insert_node(NODE *node, int key){
//t는 탐색을 위한 포인터이다.
NODE *p, *t; //p는 부모노드를 가리키는 포인터, t는 현재 노드 포인터
NODE *n; //n은 새로운 노드
t = *root; //처음 시작 시 현재 노드는 root 그 자체다.
p = NULL; //root의 부모노드는 없다. root 자체가 시초
//탐색을 먼저 수행한다.
while(t){
if(key == t->key) return; //해당 키가 이미 트리에 존재할 경우 리턴한다.
p = t; //부모 노드를 현재 노드로 설정한다. 새로운 루트노드
//서브트리의 새로운 루트노드가 등장하는 것과 같은 원리다.
if(key < p->key) //부모의 키 값과 비교
t = p->left; //현재 노드는 부모의 왼쪽 서브트리가 된다.
else
t = p->right; //현재 노드는 부모의 오른쪽 서브트리가 된다.
}
//key가 트리안에 없으므로 삽입이 가능하다.
//새로 삽입될 노드를 생성한다.
n = (NODE*)malloc(sizeof(NODE));
if(!n) return; //동적할당 실패했을 경우 return
//데이터를 복사한다.
if(p) // 부모노드가 존재할 경우
{
if(key < p->key)
p->left = n;
else
p->right = n;
}
else
*root = n; //부모노드가 없으니 새로생긴 노드가 루트 노드가 된다.
}부모노드와 현재노드에 대한 포인터를 각각 p,t로 따로 주고있다. 왜냐하면 부모노드에 대한 포인터 없이 탐색을 해나가서 NULL이 나왔다고 가정하면 여기다가 새로운 노드를 삽입할 방법이 없다. 새로운 노드를 생성해서 NULL에 붙인다는 건 말이 안된다. 무조건 그 전에 있던 부모에 대한 포인터를 알아야만 하기 때문에 이렇게 따로 둔것이다.
삭제
삭제연산은 탐색, 삽입보다는 약간 복잡하다. 삭제 결과로 자칫 이진탐색트리의 속성이 깨질 수 있기 때문이다. 삭제도 삽입과 마찬가지고 탐색을 먼저해야한다. 삭제하길 원하는 키 값이 트리 안의 어디에 위치하는지를 알아야 삭제할 수 있기 때문이다. 노드를 탐색했다면, 아래의 가능한 세가지 경우의 수를 모두 따져보아야 한다. 삭제시 발생할 수 있는 상황 3가지 이다.
-
삭제할 노드에 자식노드가 없는 경우 (삭제하려는 노드가 단말노드일 경우)
-해당 노드를 그냥 없애기만 하면 된다. 부모노드를 찾아서 부모노드 안의 해당 링크(그림의 경우 오른쪽 링크)필드를 NULL로 만들어서 연결을 끊어주면 된다. 동적으로 할당된 노드였을 경우, 메모리를 반납하고 링크 필드를 NULL로 만들어주면 된다.
-
삭제할 노드에 자식노드가 하나 있는 경우
-노드를 지우고, 해당 노드의 자식노드와 부모노드를 연결해주면 된다.
-68을 가지고 있는 노드를 삭제하고자 한다. 35를 가지고 있는 부모노드의 오른쪽 링크 필드가 99를 가리키게 수정하면 된다. 동적할당된 노드였다면 68을 먼저 반납해주고, 부모의 오른쪽 링크에 99를 연결해 주면 된다.
-
삭제하려는 노드가 두개의 서브트리를 모드 가지고 있는 경우
-18을 삭제하려 한다. 삭제한 이후에 35를 가지고 있는 부모 노드의 왼쪽 링크필드를 어떤 노드에 연결시켜야 할까? 결론부터 말하면 왼쪽 서브트리에 있는 값 중 가장 큰 값, 혹은 오른쪽 서브트리에 있는 값 중 가장 작은 값 을 가지고 있는 노드를 연결시켜주면 된다-이러한 판단의 근거는 트리의 변동성을 최소화하기 위함에 있다. 18이 있는 상태에서 중위순회를 한다고 가정해보자. 중위순회의 순서는 LVR이다. 순회를 하던 도중 12까지 이르렀다고 가정한다.12 다음에는 어딜 방문할까? 18을 방문한다. 18 다음에는 22를 방문한다. 즉, 12-18-22 순서로 방문하게 된다. 12와 22는 각각 삭제할 노드의 중위 선행자 후속자에 속한다. 이들을 선택해서 18자리를 대체하면 트리의 변동성을 최소로 할 수 있다. 딱 하나만 바꾸면 트리가 정상적으로 작동한다.
-22를 선택했다고 가정해보자. 그러면 우리가 할 일은 삭제되는 노드의 오른쪽 서브트리에서 왼쪽 자식의 링크를 타고 NULL이 나올때까지 계속 진행하면 된다. 그렇게 찾아낸 값을 35의 왼쪽 링크 필드에 이어주고 22의 왼쪽 링크 필드를 7에, 오른쪽 링크 필드를 26에 연결해주면 된다. 복잡하지만 코드를 천천히 살펴보자.
void delete_node(NODE **root, int key){
NODE *parent, *child, *suc, *suc_p, *t;
//key를 갖는 노드 t를 탐색한다. parent는 t의 부모노드이다.
parent = NULL; //시초가 되는 root의 부모는 없다.
t = *root;
//key를 갖는 노드 t를 탐색한다.
while(t != NULL && t->key != key){
parent = t; //부모를 t 값과 동일하게 준 후 t를 통해 탐색한다.
//t는 key값에 따라 왼쪽이나 오른쪽으로 내려간다.
t = (key < parent->key) ? parent->left : parent->right;
}
//탐색이 끝난 시점에서 만약 키 값이 트리에 없었다면 t는 NULL일 것이다.
if(!t){
printf("key is not in the tree");
return;
} //원하는 값이 없으므로 return 한다.
//위에서 탐색을 못했을 경우를 다뤘기 떄문에 이 아래부터는 탐색이 성공적으로 이루어졌다는 가정 하에 경우의 수를 따진다.
//첫 번째 : 단말노드 였을 경우
if(t->left == NULL && t->right == NULL){
if(parent){ //부모노드가 NULL이 아닐떄, 즉 존재할때
if(parent->left == t)
parent->left = NULL;
else
parent->right = NULL;
}
else
*root = NULL; //부모노드가 NULL이라면, 삭제하려는 노드가 루트노드다.
}
//두 번째 : 하나의 서브트리만 가지는 경우
else if((t->left == NULL) || (t->right == NULL)){
child = (t->left != NULL) ? t->left : t->right;
if(parent) {
if(parent->left == t)
parent->left = child;
else
parent->right = child;
}
else //부모노드가 NULL 이라면 삭제되는 노드가 루트노드다.
*root = child;
}
//세 번째 : 두개의 서브트리를 모두 가지는 경우
else {
//오른쪽 서브트리에서 가장 작은 값을 찾는다.
suc_p = t;
suc = t->right;
while(suc->left != NULL){
suc_p = suc;
suc = suc->left;
}
//후속자의 부모와 후속자의 자식을 연결
if(suc_p->left == suc)
suc_p->left = suc->right;
else //왼쪽 끝까지 내려왔는데 그 끝에 오른쪽 서브트리가 있을 수도 있을 경우.
suc_p->right = suc->right;
t->key = suc->key;
t = suc;
}
free(t); //옮겨준 후속자 없앰
}
위 그림의 빨간색 표시 부분이 현재 지워야할 부분 t라고 가정하고, 세번째 알고리즘을 그대로 따라가보도록 하자.
기존의 그림과 달라진 점은 맨 밑에 22노드 우측 자식노드로 23이 추가됐다는 점이다.
-
t->key = suc->key;
-
t = suc;
우리가 현재 삭제하고 싶은 노드는 18이다. 18노드를 삭제하고, 우측 서브트리에서 제일 작은 값인 22를 그 자리에 대체하고 싶다. 이러한 상황에서 만약 t->key=suc->key; 문장을 써주지 않으면 어떤 일이 발생할까? 를 생각해보면 이해가 쉬울 것이다.
써주지 않는다면, suc->left = t->left; suc->right = t->right; 작업을 해줘야 한다. 만약 이렇게 해줬을 경우 뒤에 따라나오는 문장인 t=suc;는 필요가 없다. suc를 있는 그대로 대체하고 싶다면, 삭제하고 싶은 노드가 원래 가지고 있던 왼쪽 링크필드와 오른쪽 링크필드를 그대로 suc의 링크필드에 복사해야한다. 이 작업이 번거롭다고 판단한 나머지 그냥 기존에 있던 t를 버리지 않고, 키 값을 suc의 키 값으로 대체한 것이다.
기존에 있던 suc는? free로 메모리 반납해 주면 된다. 하지만, 왜 굳이 또 t=suc; 란 문장을 넣은 걸까? 이유는 간단하다. 우리는 3가지 케이스는 if 문으로 한데 모아 다루고 있다. free(t) 부분이 if 문을 벗어난 맨 마지막에 있으므로, 세번째 케이스 또한 free(t)문을 그대로 이용할 필요가 있는 것이다. 그래야 중복된 코드 작성이 안되고 일관성이 있으니까. 그래서 t를 그대로 활용한 뒤, t가 가리키는 노드를 suc으로 대체한 후 반납하는 것이다. 마치 대리반납과 비슷한 느낌이다.
이진탐색트리의 시간복잡도 분석
이진탐색트리에서의 탐색, 삽입, 삭제 연산의 시간복잡도는 트리의 높이를 h라고 했을때 O(h)가 된다 따라서 n개의 노드를 가지는 이진탐색트리의 경우, 균형 잡힌 이진트리의 높이는 log(2n)이므로 이진탐색트리의 평균적인 경우의 시간복잡도는 O(log2n)이다.
편향 이진 트리의 경우에는 n개의 노드를 가지는 트리의 높이가 n과 같게되어 탐색, 삽입, 삭제 시간이 거의 선형 탐색과 같이 O(n)이 된다.
편향 이진트리의 경우 선형탐색에 비하여 전혀 시간적으로 이득이 없다. 이러한 최악의 경우를 방지하기 위해 트리의 높이를 log(2n)으로 한정시키는 균형 기법이 필요하다.
트리를 균형있게 만드는 기법으로는 AVL트리를 비롯한 여러 기법들이 존재한다. 균형트리의 경우 별도의 포스팅으로 다룰 예정이다.




