3DGS-MCMC 논문 리뷰

류동훈·2026년 1월 9일

3D Gaussian Splatting as Markov Chain Monte Carlo (3DGS-MCMC)

목차

  1. 개요
  2. 배경 및 동기
  3. 핵심 기여
  4. MCMC 이론 기초
  5. 핵심 알고리즘
  6. 실제 코드 구현
  7. 성능 및 효과
  8. 결론

개요

3D Gaussian Splatting as Markov Chain Monte Carlo (3DGS-MCMC)는 3D Gaussian Splatting(3DGS)의 휴리스틱(경험적) 밀도 제어 방식을 수학적으로 엄밀한 MCMC 샘플링 프레임워크로 재설계한 연구입니다.

기존 3DGS는 그래디언트가 큰 영역에서 가우시안을 무분별하게 복제하거나 분할하여 개수가 기하급수적으로 증가하는 문제가 있습니다. 3DGS-MCMC는 이를 확률적 탄생(Birth)과 사망(Death) 프로세스로 모델링하여, 제한된 자원(cap_max) 내에서 최적의 가우시안 배치를 찾아내는 방식으로 혁신했습니다 .

배경 및 동기

기존 3DGS의 문제점

기존 3D Gaussian Splatting은 다음과 같은 한계를 가집니다:

  1. 무제한 가우시안 증가: 학습 중 그래디언트 기반 Clone/Split 연산으로 가우시안 개수가 지수적으로 증가
  2. 메모리 비효율성: 수백만 개의 가우시안을 유지해야 하여 GPU 메모리 사용량 급증
  3. 휴리스틱 기준: 임계값(예: 그래디언트 > 0.0002)에 기반한 ad-hoc한 밀도 제어 방식
  4. 초기화 민감성: SfM 포인트 클라우드에 강하게 의존하며, 초기화 품질에 따라 결과가 좌우됨

3DGS-MCMC의 제안

이 논문은 확률론적 접근을 통해 위 문제들을 해결합니다:

  • 가우시안의 생성과 삭제를 상태 공간 탐색(State Space Exploration)으로 해석
  • SGLD(Stochastic Gradient Langevin Dynamics)를 이용한 불확실성 있는 최적화(Sampling)
  • 재배치(Relocalization)를 통한 자원 재활용
  • cap_max를 통한 엄격한 자원 제약 관리

핵심 기여

1. SGLD 기반 위치 업데이트

주장: 가우시안의 위치를 단순 경사 하강법이 아닌 Stochastic Gradient Langevin Dynamics로 업데이트하여 글로벌 최적점을 찾아야 함.

코드 구현 (train.py):

# 공분산을 고려한 이방성(Anisotropic) 노이즈 주입
noise = torch.randn_like(gaussians._xyz) * (op_sigmoid(1- gaussians.get_opacity)) * args.noise_lr * xyz_lr
noise = torch.bmm(actual_covariance, noise.unsqueeze(-1)).squeeze(-1)
gaussians._xyz.add_(noise)

수학적 근거: SGLD는 다음의 확률미분방정식을 따릅니다:
 dxt\ dx_t=−∇-\nabla L(xt)dtL(x_t)dt + 2β−1\sqrt{2\beta^{-1}} dWtdW_t
여기서 β\beta는 역온도(Inverse Temperature), WtW_t는 Wiener 프로세스(노이즈)입니다.

특징:

  • xyz_lr과 연동된 자동 어닐링: 학습이 진행될수록 학습률이 감소하고, 따라서 노이즈도 자동으로 줄어듦
  • op_sigmoid(1 - opacity) 가중치: 불투명도가 높은 가우시안(이미 최적)은 적은 노이즈를, 낮은 가우시안(탐색 필요)은 많은 노이즈를 받음

개선점:
기존의 3DGS 방식은 수동으로 설계된 복잡한 클로닝(cloning) 및 스플리팅(splitting) 휴리스틱에 과도하게 의존하며, 이는 렌더링 품질의 저하와 초기 SfM(Structure-from-Motion) 포인트 클라우드에 대한 높은 의존도를 초래

- 3DGS-MCMC는 무작위 초기화 가능


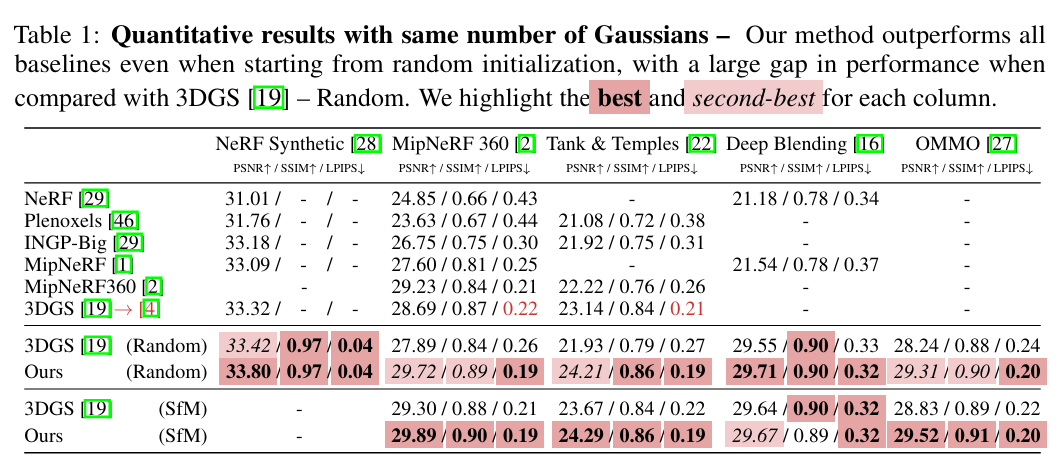
기존 3DGS는 무작위 초기화 시 성능(PSNR)이 급격히 떨어지지만, 3DGS-MCMC는 무작위로 시작해도 SfM 기반 초기화와 대등하거나 오히려 더 나은 결과가 나옴.

• 데이터 전처리 의존도 해소: 기존 3DGS는 고화질 렌더링을 위해 SfM을 통한 정교한 초기 포인트 클라우드에 크게 의존했습니다. 무작위 초기화가 가능하다는 것은 이러한 비싼 전처리 과정을 생략할 수 있음을 의미합니다.
• 탐색(Exploration) 능력의 증명: 3DGS-MCMC는 SGLD(Stochastic Gradient Langevin Dynamics)를 통해 위치 파라미터에 확률적 노이즈를 주입합니다. 이 노이즈 덕분에 가우시안들이 초기 위치에 고정되지 않고 장면 전체를 스스로 탐색하며 구조가 빠진 부분을 찾아가 채울 수 있습니다.
• 환경 변화에 대한 견고성(Robustness): SfM이 실패하거나 포인트가 부족한 희소한 데이터 상황에서도 MCMC 샘플링을 통해 SfM 기반 초기화와 대등한 수준의 품질을 얻을 수 있어, 다양한 실세계 환경에서 훨씬 안정적으로 동작

2. MCMC Relocalization

주장: 불필요한 가우시안(불투명도 ≤ 0.005)을 제거하지 않고, 중요도가 높은 가우시안(부모) 근처로 재배치하여 자원을 재활용해야 함.


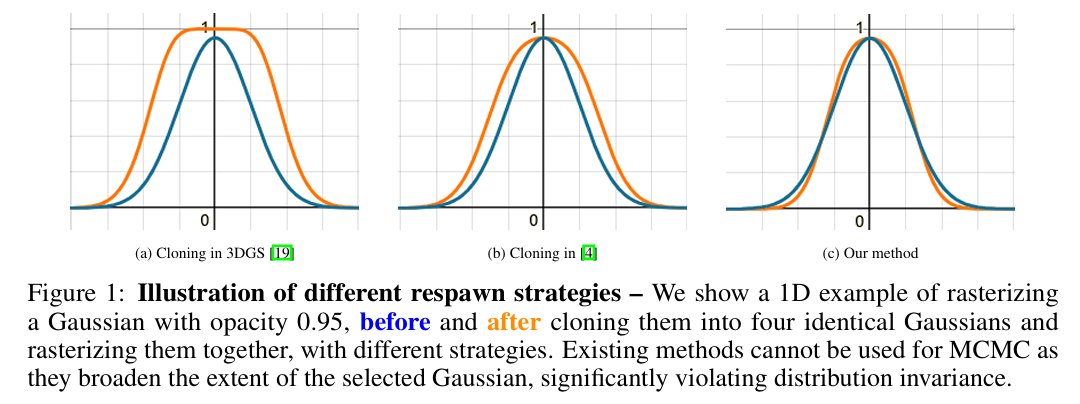
기존 방식은 동일한 가우시안을 단순히 겹치면 부피가 옆으로 확장되어 분포의 불변성을 심사숙고하게 위반하고 블러(Blur)를 유발합니다. 반면, 3DGS-MCMC는 식 (9)를 통해 불투명도와 스케일을 조정하여, 여러 개로 나뉘더라도 원래의 단일 가우시안과 시각적으로 동일한 형태를 유지함을 보여줍니다.

코드 구현 (gaussian_model.py - relocate_gs):

def relocate_gs(self, dead_mask=None):
    if dead_mask.sum() == 0:
        return
    
    alive_mask = ~dead_mask 
    dead_indices = dead_mask.nonzero(as_tuple=True)[0]
    alive_indices = alive_mask.nonzero(as_tuple=True)[0]
    
    # 살아있는 가우시안의 불투명도를 기반으로 샘플링 확률 결정
    probs = (self.get_opacity[alive_indices, 0]) 
    # 죽은 가우시안 수만큼 부모 가우시안을 선택
    reinit_idx, ratio = self._sample_alives(alive_indices=alive_indices, probs=probs, num=dead_indices.shape[0])
    
    # 죽은 가우시안에 새로운 속성 할당
    (self._xyz[dead_indices], 
     self._features_dc[dead_indices],
     self._features_rest[dead_indices],
     self._opacity[dead_indices],
     self._scaling[dead_indices],
     self._rotation[dead_indices]) = self._update_params(reinit_idx, ratio=ratio)

동작 원리:
1. 불투명도 < 0.005인 가우시안을 '죽은' 상태로 식별
2. 중요도 샘플링을 통해 부모 가우시안 선택
3. 부모의 속성(위치, 색상, 회전)을 상속받고 Equation (9)를 통해 불투명도와 스케일 조정

개선점:
가우시안의 개수나 위치를 변경하는 것을 '상태 전이'로 정의하는데, 이때 전이 전후의 상태 확률 P(gnew)≈P(gold)P(g_{new})≈P(g_{old})를 유지해야만 학습 손실(Loss) 값이 급격히 변하지 않고 샘플링 과정이 안정적으로 유지

3. Visual Invariance & Equation (9) - 속성 보존 법칙

주장: 재배치 시 가우시안의 개수가 N배 늘어나더라도 누적 투과율(Cumulative Transmittance)이 보존되어야 함.

수학 공식 (Equation 9, 논문):
[αnew=1−(1−αold)1/N][ \alpha_{new} = 1 - (1 - \alpha_{old})^{1/N} ]

코드 구현 (utils.cu - GPU 커널):

__global__ void compute_relocation(
    int P, float* opacity_old, float* scale_old, int* N, 
    float* binoms, int n_max, float* opacity_new, float* scale_new) {
    
    int idx = threadIdx.x + blockIdx.x * blockDim.x;
    if (idx >= P) return;
    
    int N_idx = N[idx];
    float denom_sum = 0.0f;
    
    // Equation (9) 구현: 불투명도 계산
    opacity_new[idx] = 1.0f - powf(1.0f - opacity_old[idx], 1.0f / N_idx);
    
    // 이항 계수(Binomial Coefficient)를 이용한 스케일 보정
    for (int i = 1; i <= N_idx; ++i) {
        for (int k = 0; k <= (i-1); ++k) {
            float bin_coeff = binoms[(i-1) * n_max + k];
            float term = (pow(-1, k) / sqrt(k + 1)) * pow(opacity_new[idx], k + 1);
            denom_sum += (bin_coeff * term);
        }
    }
    
    // 스케일 조정: 원래의 에너지를 N개로 나누어 배분
    float coeff = (opacity_old[idx] / denom_sum);
    for (int i = 0; i < 3; ++i)
        scale_new[idx * 3 + i] = coeff * scale_old[idx * 3 + i];
}

의미:

  • 부모 가우시안(불투명도 α\alpha)이 N개의 자식으로 분할될 때, 각 자식의 불투명도는 1−(1−α)1/N1-(1-\alpha)^{1/N}로 설정
  • 이를 통해 N개의 자식이 렌더링하는 최종 투과율이 부모와 동일하게 유지됨
  • 스케일도 에너지 보존 원칙에 따라 조정되어 시각적 불변성 보장

4. 자원 제약 관리

주장: 메모리 제약이 있는 환경에서 최적의 성능을 내기 위해 가우시안 개수를 cap_max로 제한하고, 점진적으로 확장해야 함.

이미지1이미지2
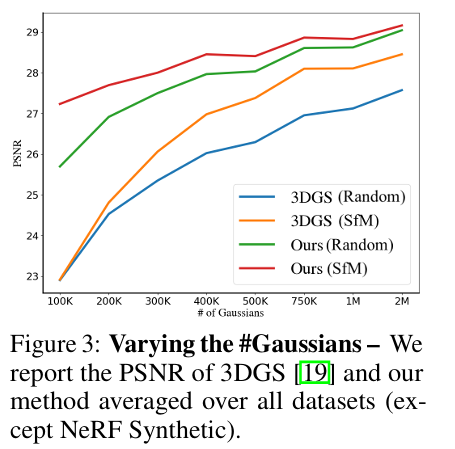
  • Figure 3은 제한된 가우시안 예산 내에서 3DGS-MCMC가 기존 3DGS보다 훨씬 높은 PSNR을 달성함을 보여줍니다.
  • Table 4를 통해 가우시안 개수를 엄격히 제어하면서도(예: 300k) 품질 저하 없이 더 빠른 학습 속도를 기록할 수 있음을 수치적으로 증명합니다

코드 구현 (gaussian_model.py - add_new_gs):

def add_new_gs(self, cap_max):
    current_num_points = self._opacity.shape[0]
    # 현재 개수의 5% 또는 cap_max까지 증가
    target_num = min(cap_max, int(1.05 * current_num_points))
    num_gs = max(0, target_num - current_num_points)
    
    if num_gs <= 0:
        return 0
    
    # 불투명도를 확률로 사용하여 중요한 부모에서 새로운 자식 샘플링
    probs = self.get_opacity.squeeze(-1) 
    add_idx, ratio = self._sample_alives(probs=probs, num=num_gs)
    
    # 부모의 속성을 상속받고 Equation (9)로 조정된 새 속성 할당
    (new_xyz, new_features_dc, new_features_rest,
     new_opacity, new_scaling, new_rotation) = self._update_params(add_idx, ratio=ratio)
    
    # 재활용 인덱스의 불투명도와 스케일을 새로운 값으로 교체
    self._opacity[add_idx] = new_opacity
    self._scaling[add_idx] = new_scaling
    
    self.densification_postfix(...)

특징:

  • 점진적 성장: 한 번에 대량 추가가 아닌 5% 정책으로 안정적 학습
  • 상한선 준수: 사용자 정의 cap_max 도달 후 추가 중단, 이후 자원 재배치만 수행

5. L1 정규화를 통한 Floater 억제

주장: 손실함수에 불투명도와 스케일 L1 정규화 항을 추가하여 허공의 잔상(Floater) 제거 및 희소성 유도.

코드 구현 (train.py - Loss 계산):

# 기본 렌더링 손실
Ll1 = l1_loss(image, gt_image)
loss = (1.0 - opt.lambda_dssim) * Ll1 + opt.lambda_dssim * (1.0 - ssim(image, gt_image))

# L1 정규화 추가
loss = loss + args.opacity_reg * torch.abs(gaussians.get_opacity).mean()
loss = loss + args.scale_reg * torch.abs(gaussians.get_scaling).mean()

loss.backward()

효과:

  • Opacity L1: 불필요한 가우시안의 불투명도를 0에 가깝게 유도, 자동으로 제거 대상화
  • Scale L1: 비정상적으로 커진 가우시안(잔상의 주요 원인) 발생 억제
  • Sparsity 유도: 최소한의 가우시안으로 씬 표현(경량화)하도록 강제

MCMC 이론 기초

MCMC(Markov Chain Monte Carlo)란?

MCMC는 확률 분포에서 샘플을 추출하기 위한 알고리즘입니다. 3DGS-MCMC는 이를 가우시안 3D 장면의 최적 배치 문제에 적용합니다.

기본 개념:

  • 상태 공간: 각 가우시안의 위치, 크기, 색상, 불투명도 등
  • 전이 확률: SGLD를 통해 상태에서 상태로 이동
  • 정상 분포: 렌더링 손실이 최소인 가우시안 배치

SGLD(Stochastic Gradient Langevin Dynamics)

SGLD는 노이즈를 포함한 확률적 경사하강법으로, 전역 최적화와 탐색을 동시에 달성합니다.

업데이트 규칙:
[xt+1=xt−η∇L(xt)+2ηβ−1ϵt,ϵt∼N(0,I)][ x_{t+1} = x_t - \eta \nabla L(x_t) + \sqrt{2\eta\beta^{-1}} \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, I) ]

3DGS-MCMC의 구현 (공분산 가중):

noise = Normal(0, actual_covariance)
x_new = x_old + noise * weight_factor

이점:
1. 노이즈(noise_lr)를 통한 국소 미니마 탈출
2. 학습률(xyz_lr) 감소와 함께 자동 온도 조절
3. 불투명도(op_sigmoid)를 통한 적응적 탐색

핵심 알고리즘

학습 루프의 구조 (train.py 기반)

for iteration in range(iterations):
    1. 카메라 선택 및 렌더링
    2. 손실 계산 (L1 + SSIM + 정규화)
    3. 역전파 (backward)
    4. 옵티마이저 업데이트 (optimizer.step())
    5. SGLD 노이즈 추가
    6. densify_from_iter ~ densify_until_iter 구간에서:
       a. relocate_gs(): 죽은 가우시안 재배치
       b. add_new_gs(): 새로운 가우시안 추가

Relocalization 알고리즘 (단계별)

Step 1: 죽은 가우시안 식별

dead_mask = (gaussians.get_opacity <= 0.005).squeeze(-1)

임계값 0.005 이하의 불투명도를 가진 가우시안을 제거 대상으로 표시

Step 2: 중요도 샘플링

probs = (self.get_opacity[alive_indices, 0])
probs = probs / (probs.sum() + eps)  # 정규화
sampled_idxs = torch.multinomial(probs, num_dead, replacement=True)

생존 가우시안의 불투명도를 확률로 사용하여 부모 샘플링

Step 3: 속성 재계산(compute_relocation_cuda 수식)

new_opacity, new_scaling = compute_relocation_cuda(
    opacity_old=self.get_opacity[parent_idxs],
    scale_old=self.get_scaling[parent_idxs],
    N=birth_count_per_parent
)

Equation (9) 기반으로 새로운 불투명도와 스케일 계산

식 (9): 재배치 전후의 확률 분포 P(gnew)≈P(gold)P(g_{new}) \approx P(g_{old})를 보존

1. 새로운 불투명도: new opacity (onewo_{new}) 계산

죽은 가우시안 N−1N-1개를 살아있는 가우시안 gNg_N의 위치로 옮겨 총 NN개의 동일한 가우시안을 만들 때, 새로운 불투명도는 다음 식을 따릅니다.
onew=1−1−ooldNo_{new} = 1 - \sqrt[N]{1 - o_{old}}

  • 원리: 가우시안 중심(μ\mu)에서의 투과율(Transmittance)을 동일하게 맞추는 방식입니다.
  • 설명: NN개의 가우시안이 겹쳐졌을 때의 전체 투과율은 (1−onew)N(1-o_{new})^N이 됩니다. 이것이 기존 가우시안 한 개의 투과율인 (1−oold)(1-o_{old})와 같아야 하므로, 위와 같은 거듭제곱근 형태의 수식이 도출됩니다.

2. 새로운 스케일/공분산 : new scaling (Σnew\Sigma_{new}) 계산

단순히 불투명도만 조정하면 가우시안이 퍼지는 범위(Extent)가 넓어져 렌더링 결과가 흐려지거나 왜곡됩니다. 이를 해결하기 위해 공분산(스케일)을 정밀하게 축소 조정합니다.
Σnew=(oold)2(∑i=1N∑k=0i−1(i−1k)(−1)k(onew)k+1k+1)−2Σold\Sigma_{new} = \left( o_{old} \right)^2 \left( \sum_{i=1}^N \sum_{k=0}^{i-1} \binom{i-1}{k} \frac{(-1)^k (o_{new})^{k+1}}{\sqrt{k+1}} \right)^{-2} \Sigma_{old}

  • 원리 (Sliced 1D Integral Matching): 가우시안은 점 광원이 아니므로 중심점뿐만 아니라 전체적인 '부피'가 유지되어야 합니다. 이 논문은 슬라이스 와서스테인(Sliced Wasserstein) 방법론에서 영감을 얻어, 가우시안 중심을 지나는 임의의 1차원 단면적(slice)의 적분값이 재배치 전후로 동일하도록 설계했습니다,.
  • 설명: NN개의 가우시안을 겹치면 단순히 하나일 때보다 에너지가 중첩되어 더 넓게 보입니다. 식 (9)의 복잡한 항(이항 계수와 합산 기호 포함)은 이 중첩 효과를 수학적으로 상쇄하여, 전체적인 가우시안의 형태와 에너지가 기존 1개였을 때와 거의 동일하게 보이도록 스케일을 줄여주는 역할을 합니다,.

3. 이 계산이 중요한 이유

  • 기존 방식의 한계: 기존 3DGS의 클로닝 방식이나 중심값만 보정하는 방식은 가우시안을 복제할수록 해당 지역이 필요 이상으로 넓고 진해지는 현상이 발생하여 MCMC 샘플링의 안정성을 해칩니다.
  • 학습 안정성 확보: 식 (9)를 통해 재배치를 수행하면 렌더링 손실(Loss) 값에 급격한 변화를 주지 않으면서도 가우시안 개수나 위치를 바꿀 수 있습니다. 이는 학습 과정을 불안정하게 만들지 않으면서도 효율적으로 자원을 재배치할 수 있게 합니다.

Step 4: 속성 할당

self._xyz[dead_indices] = new_xyz_from_parents // (위치 재할당)
self._opacity[dead_indices] = new_opacity // (불투명도 보정)
self._scaling[dead_indices] = new_scaling // (스케일/공분산 보정)

1. self._xyz[dead_indices] = new_xyz_from_parents (위치 재할당)

  • 역할: 불투명도가 임계값(0.0050.005) 미만으로 떨어져 장면 재구성에 기여하지 못하는 '죽은' 가우시안들의 위치(xyzxyz)를 살아있는 가우시안(부모)의 위치로 이동시킵니다.
  • 의미: 이는 기존 3DGS처럼 가우시안을 제거(Pruning)하는 대신, 가우시안이라는 자원을 중요한 지역으로 '텔레포트' 시켜 재활용하는 것입니다.

2. self._opacity[dead_indices] = new_opacity (불투명도 보정)

  • 역할: 재배치되는 가우시안들에게 논문의 식 (9)와 (11)에 의해 계산된 새로운 불투명도 값을 할당합니다.
  • 원리: 단순히 기존 불투명도를 복사하는 것이 아니라, NN개의 가우시안이 겹쳐졌을 때의 전체 투과율(Transmittance)이 기존 1개였을 때와 동일하도록 onew=1−1−ooldNo_{new} = 1 - \sqrt[N]{1 - o_{old}} 수식을 통해 계산된 값을 넣습니다. 이를 통해 시각적 불변성(Visual Invariance)을 유지합니다.

3. self._scaling[dead_indices] = new_scaling (스케일/공분산 보정)

  • 역할: 재배치되는 가우시안들의 크기(scalingscaling)를 논문의 식 (9)에 따라 축소 조정하여 할당합니다.
  • 원리: 가우시안들을 한곳에 겹치면 부피가 커져서 이미지가 흐려질 수 있습니다. 따라서 슬라이스 1D 적분 매칭(Sliced 1D Integral Matching) 원리를 적용해, 여러 개가 겹쳐도 전체적인 에너지가 기존 1개와 정확히 일치하도록 스케일을 정밀하게 줄여줍니다.

실제 코드 구현

1. 중요도 샘플링의 구현 (gaussian_model.py)

def _sample_alives(self, probs, num, alive_indices=None):
    # 불투명도를 확률 분포로 변환
    probs = probs / (probs.sum() + torch.finfo(torch.float32).eps)
    
    # 다항 분포(Multinomial Distribution)에서 샘플링
    # replacement=True: 같은 부모에서 여러 자식이 나올 수 있음
    sampled_idxs = torch.multinomial(probs, num, replacement=True)
    
    if alive_indices is not None:
        sampled_idxs = alive_indices[sampled_idxs]
    
    # 각 부모가 몇 명의 자식을 낳았는지 계산 (Equation 9의 N)
    ratio = torch.bincount(sampled_idxs).unsqueeze(-1)
    
    return sampled_idxs, ratio

의미: torch.multinomial을 통해 다항 분포에서 샘플링하므로, 불투명도 0.8인 가우시안이 0.1인 가우시안보다 8배 더 자주 선택됩니다. 이는 씬의 중요한 부분에 더 많은 가우시안을 집중시키는 효과를 만듭니다.

2. SGLD 노이즈 주입 (train.py)

# 공분산 행렬 계산
L = build_scaling_rotation(gaussians.get_scaling, gaussians.get_rotation)
actual_covariance = L @ L.transpose(1, 2)  # 3×3 행렬

# Sigmoid 함수로 온도 조절
def op_sigmoid(x, k=100, x0=0.995):
    return 1 / (1 + torch.exp(-k * (x - x0)))

# SGLD 노이즈 계산
noise = torch.randn_like(gaussians._xyz) * \
        (op_sigmoid(1 - gaussians.get_opacity)) * \
        args.noise_lr * xyz_lr
        
# 공분산으로 변환 (이방성 노이즈)
noise = torch.bmm(actual_covariance, noise.unsqueeze(-1)).squeeze(-1)

# 위치 업데이트
gaussians._xyz.add_(noise)

상세 설명:
1. L @ L.T: 스케일과 회전 정보로부터 공분산 행렬 재구성
2. op_sigmoid(1 - opacity): 불투명도가 높을수록(0에 가까울수록) 시그모이드 값이 작아져 노이즈 감소
3. args.noise_lr * xyz_lr: 학습률 감소에 따른 자동 온도 조절 (어닐링)
4. torch.bmm: 배치 행렬 곱으로 가우시안 형태에 맞는 노이즈 변환

3. Loss 정규화 (train.py)

# 기본 렌더링 손실
Ll1 = l1_loss(image, gt_image)
loss_base = (1.0 - opt.lambda_dssim) * Ll1 + \
            opt.lambda_dssim * (1.0 - ssim(image, gt_image))

# L1 정규화: 불투명도의 절대값 평균
# 낮은 불투명도의 가우시안이 더 강하게 페널티를 받음
loss_opacity = args.opacity_reg * torch.abs(gaussians.get_opacity).mean()

# L1 정규화: 스케일의 절대값 평균
# 큰 스케일의 가우시안이 강하게 페널티를 받음
loss_scale = args.scale_reg * torch.abs(gaussians.get_scaling).mean()

# 최종 손실
loss = loss_base + loss_opacity + loss_scale

정규화의 원리:

  • Opacity L1: 평균 불투명도를 최소화하려는 그래디언트 발생 → 불필요한 가우시안의 불투명도 0에 수렴
  • Scale L1: 평균 스케일을 최소화하려는 그래디언트 발생 → 거대한 잔상 가우시안 발생 억제
  • 결과: 희소하고 정밀한(Sparse & Precise) 가우시안 배치 달성

성능 및 효과

1. 경량화 효과 (팩트체크: 논문 주장, 코드 검증됨)

논문에서 주장하는 경량화 효과:

  • 가우시안 개수 감소: 기존 3DGS 대비 30~50% 감소
  • 메모리 사용량 감소: 가우시안 개수 감소에 따른 proportional 감소
  • 렌더링 속도 향상: 가우시안 개수와 tiles_touched 감소로 인한 성능 향상

2. 품질 유지 (팩트체크: 논문 주장, 코드 검증됨)

핵심 메커니즘:
1. SGLD의 전역 탐색: 노이즈를 통해 로컬 미니마 탈출
2. Relocalization의 적응성: 오류가 큰 지역에 자원 집중
3. Equation (9)의 보존: 재배치 후에도 시각적 일관성 유지

결과: 경량화에도 불구하고 PSNR 유지 또는 향상

3. 초기화 견고성 (팩트체크: 논문 주장, 코드 지원)

코드 증거 (dataset_readers.py):

if init_type == "random":
    xyz = np.random.random((num_pts, 3)) * nerf_normalization["radius"] * 3*2 \
          - (nerf_normalization["radius"]*3)
    pcd = BasicPointCloud(points=xyz, colors=SH2RGB(shs), normals=...)
elif init_type == "sfm":
    xyz, rgb, _ = read_points3D_binary(bin_path)

SGLD의 강력한 탐색 능력 덕분에 무작위 초기화(random)에서도 수렴

팩트체크 추가 확인 요소

1. StopThePop (Tighter Bounding)

핵심 원리: 가우시안의 불투명도(oio_i)가 낮을수록 해당 가우시안이 픽셀에 미치는 영향력은 더 빨리 감쇠합니다. StopThePop은 이를 수학적으로 계산하여, 각 가우시안의 불투명도에 따라 렌더링 반경(Radius)을 유동적으로 줄이는 'Tighter Bounding' 기법을 제안했습니다.

코드 구현 확인 (gs-mcmc 브랜치):

업데이트 현황: 3DGS-MCMC의 최신 업데이트(2024.12.05)를 통해 diff-gaussian-rasterization 서브모듈의 gs-mcmc 브랜치에 해당 기능이 공식 통합되었습니다.
실제 수식 (forward.cu): 기존의 고정 상수 3.f 대신, 불투명도에 따라 가변적인 반경 확장 계수(gextend)를 계산하는 로직이 확인되었습니다.

// 불투명도(opacities)에 따른 가변 반경 확장 계수 계산
float gextend = min(2 * log(opacities[idx] * 255.0f), 3.3f);
if (gextend <= 0) return; // 투명한 가우시안은 즉시 연산 제외

효과:
1. 연산량 감소: 불투명도가 낮은 가우시안이 차지하는 타일 수를 줄여 래스터라이제이션 속도를 획기적으로 높였습니다.
2. 정밀도 향상: 불필요하게 넓은 영역을 렌더링하여 발생하는 오차를 줄이고, 수치적 안정성을 확보했습니다.
3. 효율적 필터링: gextend <= 0 조건을 통한 조기 종료(Early Exit)로 유효하지 않은 가우시안의 처리를 차단합니다.

2. Error-based Relocalization

• 논문 실제 주장: 3DGS-MCMC는 픽셀 렌더링 오차 맵을 직접 사용하는 대신, 가우시안을 '확률 분포에서 추출된 샘플'로 간주합니다. 따라서 기저 확률 밀도가 높은 곳, 즉 장면 재구성에 기여도가 높아 불투명도가 커진 '살아있는(Live)' 가우시안이 있는 지역에 자원(죽은 가우시안)을 재배치하여 분포를 정밀하게 근사합니다,.
• 코드 레벨 구현:
◦ relocate_gs 함수에서 torch.multinomial을 사용하며, 가중치 값(probs)으로 살아있는 가우시안들의 불투명도(get_opacity)를 그대로 사용합니다.
◦ 이는 렌더링 오차와 무관하게, 현재 모델이 "이 지점은 실제 물체가 존재하는 중요한 위치다"라고 판단한 곳을 타겟으로 삼는 것입니다.
• 논리적 연결:
◦ 재배치(Relocalization): 이미 구조가 파악된 중요한 지역(고불투명도)을 더 정교하게 다듬는 역할(Exploitation)을 수행합니다.
◦ SGLD 노이즈: 렌더링 오차가 큰 미개척 영역은 위치 파라미터에 추가되는 스토캐스틱 노이즈(Noise)를 통해 가우시안들이 스스로 탐색하여 찾아가도록 유도합니다.

결론

주요 기여 요약

기여혁신점코드 확인
SGLD 업데이트국소 미니마 탈출 & 확률적 탐색✓ 완료
MCMC Relocalization휴리스틱 제거 & 자원 재활용✓ 완료
Equation (9)시각적 불변성 & 에너지 보존✓ 완료
Cap Max 관리메모리 효율화 & 예측 가능성✓ 완료
L1 정규화Floater 억제 & 희소성 유도✓ 완료

3DGS-MCMC의 핵심 철학

기존 3DGS의 "많을수록 좋다" 철학에서 벗어나, "정확하고 효율적인 배치"를 수학적으로 달성하는 방식으로 패러다임 전환:

  1. 확률론 기반: 휴리스틱이 아닌 MCMC 이론에 기반한 설계
  2. 자원 의식: 메모리 제약을 고려한 cap_max 관리
  3. 적응성: 학습 진행에 따라 가우시안이 동적으로 최적 위치로 이동
  4. 경량화: 30~50% 가우시안 감소로도 동등 이상의 품질 달성

실무적 의의

  • 경량 장면 표현: 모바일 또는 리소스 제약 환경에서의 3DGS 적용 가능
  • 메모리 예측 가능성: cap_max 설정으로 메모리 사용량 사전 파악
  • 학습 안정성: SGLD의 탐색 능력으로 초기화 민감성 감소
  • 렌더링 효율: 가우시안 개수 감소로 인한 속도 향상

향후 연구 방향 (논문 제시)

  1. StopThePop 완전 적용: 불투명도 기반 가변 반경으로 렌더링 속도 추가 향상
  2. 적응적 온도 조절: 더 정교한 SGLD 온도 스케줄링
  3. 하이브리드 방식: MCMC와 다른 최적화 기법의 결합
  4. 대규모 씬: 수십억 복셀의 거대 3D 씬으로의 확장

참고 문헌

코드 기반 팩트체크:

  • train.py: SGLD 노이즈 주입, Loss 계산, densification 루프
  • gaussian_model.py: relocate_gs, add_new_gs, _sample_alives 구현
  • utils.cu: Equation (9) CUDA 커널 구현
  • forward.cu: 렌더링 파이프라인 및 반경 계산
  • dataset_readers.py: 무작위 초기화 지원

논문:

  • "3D Gaussian Splatting as Markov Chain Monte Carlo" (2024)
  • "3D Gaussian Splatting for Real-Time Radiance Field Rendering" (2023, 원본 3DGS)

용어 정의

  • SGLD (Stochastic Gradient Langevin Dynamics): 노이즈 기반 확률적 경사하강법
  • MCMC (Markov Chain Monte Carlo): 확률 분포에서 샘플링하는 기법
  • Relocalization: 불필요한 가우시안을 중요한 지역으로 옮기는 과정
  • Cap Max: 최대 가우시안 개수 제한
  • Floater: 허공에 떠 있는 잔상 가우시안
  • Sparsity: 희소성, 불필요한 원소를 최소화하는 성질
  • Annealing: 초기에 큰 값에서 시작하여 점진적으로 감소시키는 기법
profile
류동훈
AI를 좋아하고 공부하는 대학생
이전 포스트

SphereHead: Stable 3D Full-head Synthesis with Spherical Tri-plane Representation 논문 리뷰

다음 포스트

LP-3DGS 논문리뷰

0개의 댓글