[알고리즘] Big-O 표기법

시간 복잡도와 공간 복잡도

알고리즘을 설계할 때 가장 중요한 요소 중 하나는 바로 효율성이다. 알고리즘의 효율성은 크게 시간 복잡도와 공간 복잡도로 나눌 수 있으며, 이 두 가지는 알고리즘의 성능을 결정짓는 요소이다.

• 공간 복잡도

  공간 복잡도는 알고리즘을 실행하는 데 필요한 메모리 공간의 양을 나타낸다.

  • 메모리 자원이 제한된 환경에서는 공간 복잡도를 최적화하여 메모리 사용량을 줄임으로써 시스템의 전반적인 성능을 향상시켜야 한다.

  • 요즘은 하드웨어 성능이 과거에 비해 비약적으로 발전하여 메모리 문제에 대해 크게신경 쓰지 않아 공간복잡도보다 시간복잡도를 중요하게 다룬다.

• 시간 복잡도

  시간 복잡도는 알고리즘을 실행하는 데 걸리는 시간과 입력 데이터의 크기 사이의 관계를 나타낸다.

  • 정확히는 알고리즘의 속도는 시간이 아닌 단계로 측정한다. 컴퓨터의 성능에 따라 똑같은 연산을 하더라도 시간은 모두 다르기 때문이다.
  • 시간복잡도의 표기방법

    Big-O: 최악의 실행 시간을 표기
    Big-Ω: 최상의 실행 시간을 표기
    Big-θ: 평균 실행 시간을 표기

  • 시간복잡도를 표기할 때는 가장 큰 영향력이 있는 항만 표시하며 계수와 상수항은 무시한다.
    어떤 알고리즘이 $O(5N^3+N^2+3N+9)$의 복잡도를 가졌으면 $O(N^3)$으로 표기한다.
  • 시간 복잡도는 데이터 원소 $N$개에 대한 알고리즘 단계 수를 나타낸다. 하지만 정확한 단계수가 아닌 데이터가 늘어날 때의 단계수가 어떻게 증가하지 나타낸다.
    예를 들어 테이터가 몇개가 있더라도 항상 5단계가 걸리는 알고리즘이 있다면 $O(5)$가 아닌 $(1)$로 표기를 한다.

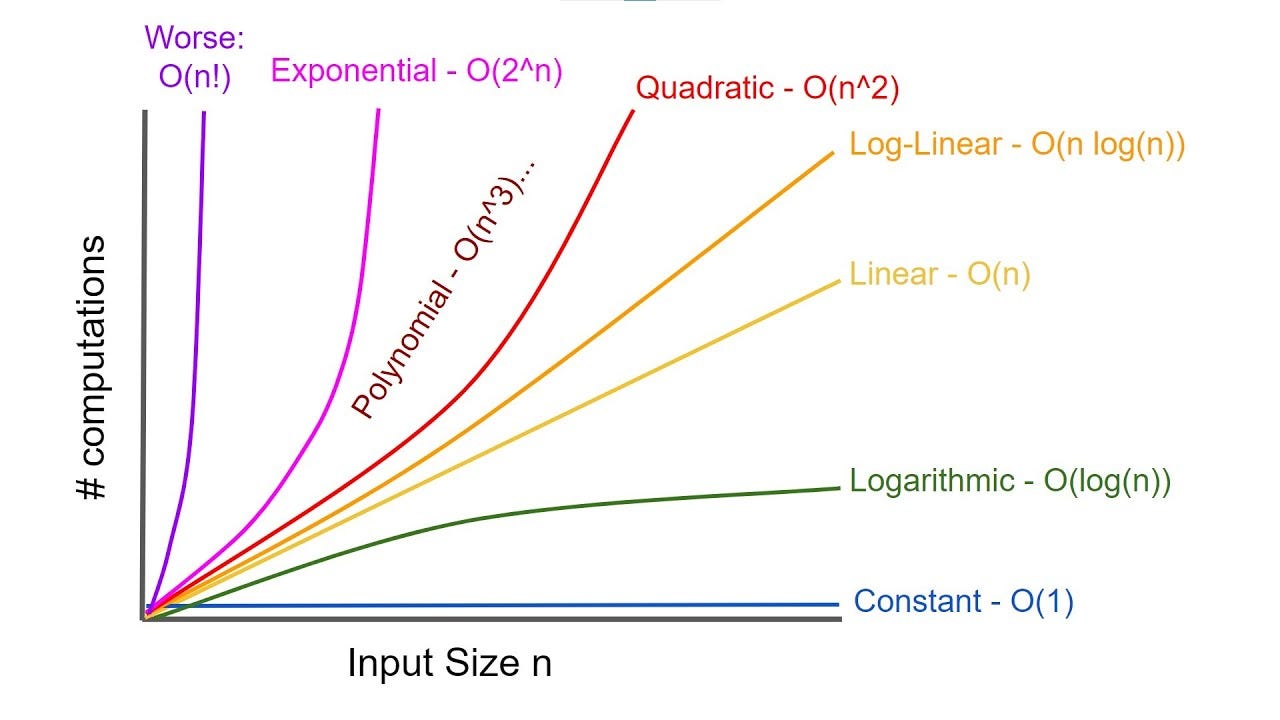
Big-O 표기법

실행 속도: $O(1) < O(log N) < O(N) < O(N log N) < O(N^2) < O(2^N)$
상수 함수 < 로그 함수 < 선형 함수 < 다항 함수 < 지수 함수

1. $O(1)$ 상수 함수
   입력 데이터의 크기에 상관없이 실행시간은 항상 동일하다.
   예시: Stack의 Push, Pop

2. $O(logN)$ 로그 함수
   컴퓨터 과학에서 $O(logN)$는 $O(log_2N)$를 줄여 부른것이다.
   입력 데이터의 크기가 커질수록 실행시간이 로그만큼 짧아진다.
   연산이 한번 실행될 때마다 데이터의 크기가 절반으로 감소된다.
   예시: 이진검색, 이진트리

3. $O(N)$ 선형 함수
   입력 데이터의 크기에 비례해 실행시간이 선형적으로 증가한다.
   예시: for문

4. $O(N logN)$ 선형로그 함수
   로그함수와 마찬가지로 $O(NlogN)$는 $O(Nlog_2N)$를 줄여 부른것이다.
   입력 데이터가 많아질수록 처리 시간이 로그 배만큼 더 늘어난다.
   예시: 퀵 정렬(Quick Sort), 합병 정렬(Merge Sort), 힙 정렬(Heap Sort)

5. $O(N^2)$ 다항 함수
   입력 데이터가 많아질수록 처리시간이 급수적으로 증가한다.
   예시: 삽입 정렬(Insertion Sort), 버블 정렬(Bubble Sort), 선택 정렬(Selection Sort), 이중for문

6. $O(2^n)$, 지수
   입력 데이터가 많아질수록 처리시간이 기하급수적으로 증가한다.
   주로 재귀적 알고리즘에서 발생
   예시: 피보나치(Fibonacci) 수열(메모지에이션 기법을 활용하면 시간복잡도는 $O(N)$)

# 재귀 방식으로 구현한 피보나치
def fibonacci_recursive(n):
	if n <= 1:
    	return n
    return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

# 동적 프로그래밍을 사용한 피보나치
def fibonacci(n, memo = {}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
    return memo[n]