자료구조 (Data Structure)

1. 배열 (Array)

같은 성격을 가진 변수들을 하나로 묶어서 저장하는 자료구조 (연속된 메모리 공간을 할당)

• 배열을 사용하면 같은 성격을 가진 변수들을 하나로 묶어서 사용이 가능해 코드를 쉽고 효율적으로 작성이 가능하다.
• 배열은 인덱스와 인덱스에 대응하는 데이터(요소)들로 이루어진 자료 구조를 나타낸다.
• index는 0부터 시작한다.

index	0	1	2	3	4	5	6	7	8	9	10
Element	37	78	87	36	76	27	45	93	23	12	66

• A라는 배열이 있을 때 배열의 각 원소에 접근할때는 인덱스를 사용한다.
  A[n] 형식으로 접근하며(n은 index), 이때 A[n]은 A배열의 n번째 원소가 아닌 (n+1)번째 원소이다. (인덱스는 0부터 시작하기 때문)
  7번째 원소를 읽고 싶다면 A[6]로 접근하여 45라는 값을 읽어낸다.

배열의 시간복잡도

• 접근(읽기)
  • index로 접근하여 해당 값을 읽기 때문에 시간복잡도는 $O(1)$
• 검색(값 가져오기)
  • 원하는 값을 찾고 싶을 때 어느 index있는지 모른다면, 최악의 경우 전체를 검색해야 하므로 시간 복잡도는 $O(N)$
  • 원하는 값의 index를 알고 있다면 시간복잡도는 $O(1)$
• 삽입, 삭제
  • 해당 인덱스를 찾아야 한다면 시간 복잡도는 $O(N)$
  • 삽입(삭제)를 하고 싶은 index를 정확히 알고 있더라도 시간복잡도는 $O(N)$이다.
    이유는 다음과 같다.

  예를들어 10개의 원소를 가지는 배열이 있다 가정하고 5번째 자리에 새로운 원소를 삽입하고자 한다면 기존에 있던 총 6개의 원소(5번째 원소부터 10번째 원소)가 이동해야 하기 때문이다.
  이러한 경우 삽입자체에는 1단계만 수행되지만, 삽입을 위해 데이터를 이동하여 빈 메모리 공간을 만드는데 6단계가 더 필요하기 때문이다 (배열은 연속된 메모리 공간이기 때문).

정적배열과 동적 배열

• 정적 배열 (Static Array)
  • 배열 크기를 미리 정해야 함. (C언어의 배열)
  • 크기 고정, 크기 초과 시 새 배열 생성 필요
• 동적 배열 (Dynamic Array)
  • 크기 초과 시 자동으로 확장
    예시: (Python의 List, Java의 ArrayList)

---

2. 스택 (Stack)

데이터를 차곡차곡 쌓아 올린 형태의 자료구조

• LIFO(Last Input First Out) 방식으로 마지막으로 입력된 데이터부터 처리한다.
• 삽입(push)은 스택의 끝에서만 이루어지며, 삭제(pop)도 마찬가지로 끝에서 이루어진다.
• 스택은 데이터들을 마치 접시를 위로 쌓은 것과 같아 스택의 끝을 top, 시작을 bottom이라 한다.

스택의 시간복잡도

• 읽기
  • 가장 위에 있는 데이터를 읽어내므로 시간복잡도는 $O(1)$
• 삽입, 삭제
  • 가장 위에서 삽입, 삭제가 이루어지므로 시간복잡도는 $O(1)$
• 검색
  • 특정 데이터를 찾을 때까지 pop이 계속진행되어 시간복잡도는 $O(N)$

스택의 활용 사례

• 함수 호출 스택 (재귀 호출 시 사용)
• 브라우저의 뒤로 가기 기능
• 괄호 짝 맞추기 문제

---

3. 큐 (Queue)

데이터가 줄지어 있는 형태의 자료구조

• FIFO(First Input First Out) 방식으로 가장 처음 입력된 데이터부터 처리한다.
• 삽입(Enqueue)은 큐의 끝에서만 이루어지며, 삭제(Dequeue)는 가장 앞쪽에서 이루어진다.
• 큐는 줄서있는 형태와 같아 큐의 시작을 front, 끝을 back이라 한다.

큐의 시간복잡도

• 읽기
  • 가장 앞에 있는 데이터를 읽어내므로 시간복잡도는 $O(1)$
• 삽입, 삭제
  • 삽입은 가장 뒤에서, 삭제는 가장 앞에서 이루어지므로 시간복잡도는 $O(1)$
• 검색
  • 특정 데이터를 찾을 때까지 dequeue가 계속진행되어 시간복잡도는 $O(N)$

큐의 활용 사례

• 프로세스 관리 (운영체제의 작업 대기열)
• 프린터 작업 순서 관리
• 그래프의 너비 우선 탐색(BFS)

---

4. 연결 리스트 (Linked list)

배열과 비슷해 보이지만 내부적으로 크게 다르다.
각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장한 자료구조

• 배열은 연속된 메모리 공간을 할당 받지만, 연결 리스트의 경우 데이터가 메모리 곳곳에 흩어져있다.
• 각 노드에는 데이터와 다음 노드의 메모리주소(포인터)를 포함하고 있다.
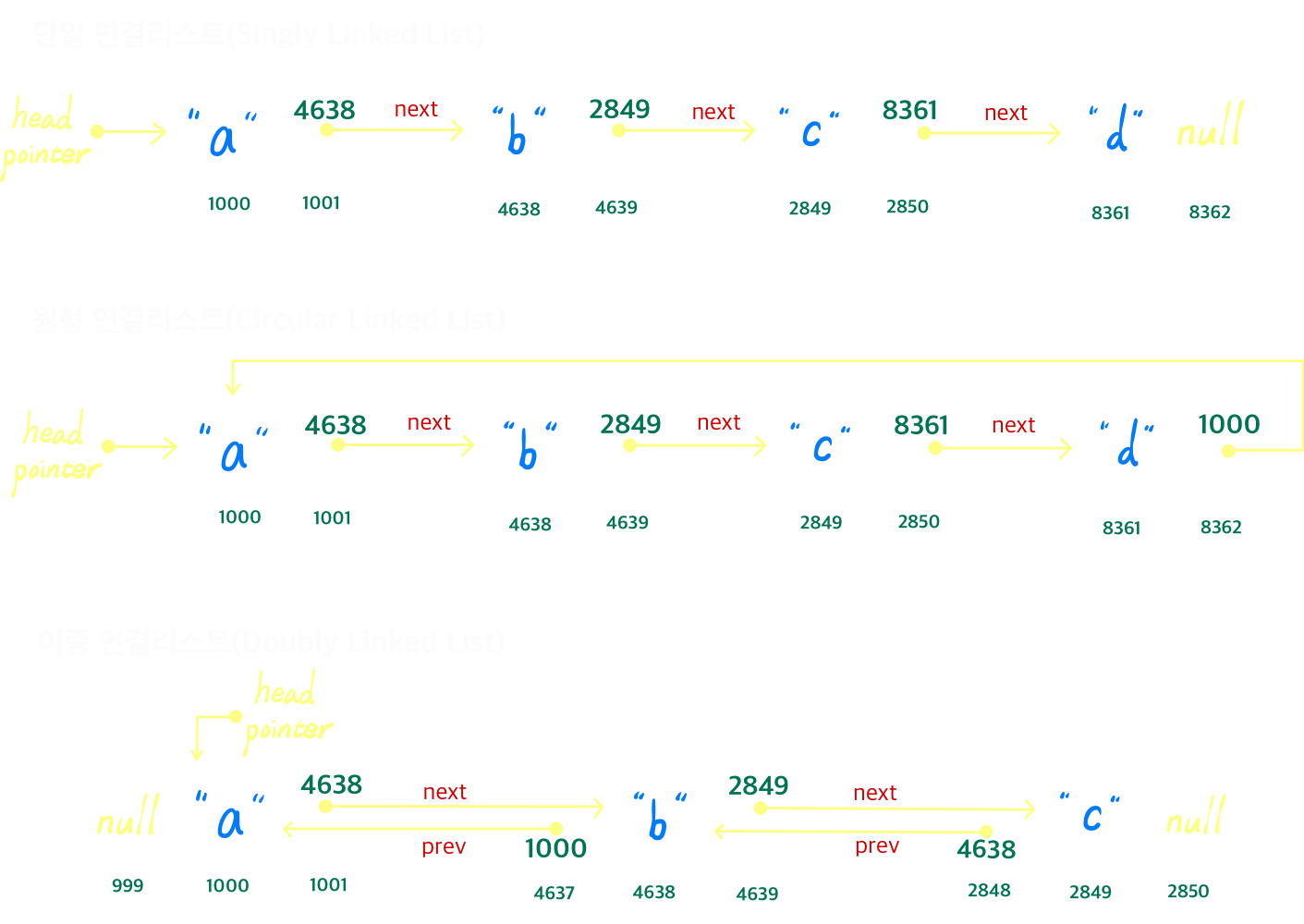
• 연결리스트의 첫번째 노드를 head, 마지막 노드를 tail이라고 한다.
• tail의 next field null을 저장하여 연결리스트의 끝임을 표기한다.
  원형 연결리스트의 경우 head의 주소값을 저장
  이중 연결리스트의 경우 헤드의 prev field와 테일의 next field에 null 저장
• 이중원형 연결리스트를 구현하고 싶다면 헤드의 prev field에 테일의 주소값, 테일의 next field에 헤드의 주소값을 저장하면 된다.
  

연결리스트의 시간복잡도

• 읽기, 검색
  • 데이터를 읽거나 검색하기 위해서는 순차적으로 탐색해야하므로 시간복잡도는 $O(N)$
• 삽입, 삭제
  • 삽입, 삭제 행위 자체는 주소값만 변경하면 되기 때문에 시간복잡도는 $O(1)$이지만, 삽입(삭제) 하려는 위치에 따라 시간복잡도는 달라진다.
  • 삽입, 삭제가 헤드위치라면 시간복잡도는 $O(1)$
  • 삽입, 삭제가 중간노드에서 이루어진다면 순차적으로 탐색하여 해당위치로 이동해야 하기 때문에 시간복잡도는 $O(N)$
  • 원형 연결리스트의 경우 삽입, 삭제가 헤드나 테일에서 이루어진다면 시간복잡도는 $O(1)$

연결리스트의 활용 사례

• 파일 시스템의 디렉토리 구조
• 브라우저 히스토리 관리

연결리스트와 배열의 차이점

• 연결리스트는 배열과 달리 데이터를 삽입또는 삭제할 때 메모리 재구성이 필요가 없어 메모리를 효율적으로 사용이 가능하다.
• 배열은 생성할 때 크기를 정하여 연속된 메모리 주소를 할당받아 데이터를 배열의 크기만큼만 저장이 가능하다. 이러한 이유로 배열은 static(정적) 자료구조이다.
• 연결리스트는 크기를 미리 정할 필요가 없고, 메모리주소가 흩어져 있어도 선형구조로 데이터 저장이 가능하여 크기에 제한이 없다. 이러한 이유료 연결리스트는 dynamic(동적) 자료구조이다.

---

5. 해시 테이블 (Hash table)

key와 value로 데이터를 저장하는 자료구조

• 각각의 키에 해시함수를 적용하여 고유한 해시값을 받고 이를 인덱스로 활용하여 값(value)를 저장한다. 이때 저장되는 배열을 bucket이라고 한다.
  

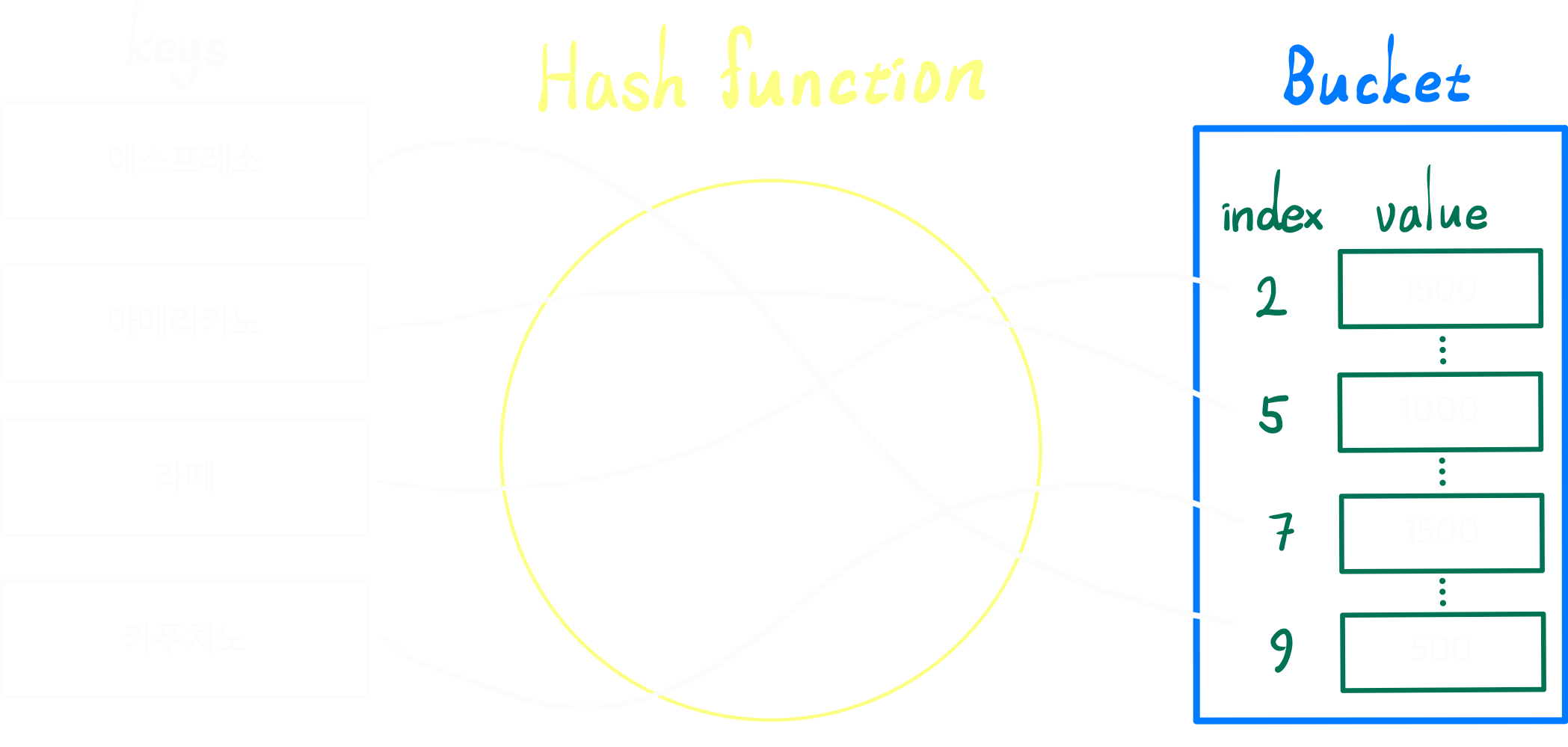
• 예를들어 카페의 메뉴이름과 가격을 배열로 만든다면 다음과 같이 생성할 수 있다.

# 해당 언어는 python으로 작성하였습니다.
cafe_menu = [["에스프레소", 500], ["아메리카노", 1000], ["라떼", 1500], ["카푸치노", 1500]]

         이때 라떼의 가격을 확인하고 싶다면 선형검색을 수행해야 하므로 $O(N)$의 단계가 걸린다.

# 해당 언어는 python으로 작성하였습니다.
for i in range(len(cafe_menu)):
  if cafe_menu[i][0] == "라떼":
    latte_price = cafe_menu[i][1]
print(latte_price)

• 이제 다음과 같이 해시테이블을 생성한 후 라떼의 가격을 한다면 다음과 같이 $O(1)$의 단계가 걸린다.

# 해당 언어는 python으로 작성하였습니다.
cafe_menu = {"에스프레소":500, "아메리카노":1000, "라떼":1500, "카푸치노":1500}
latte_price = cafe_menu["라떼"]
print(latte_price)

• 해시값이 동일하게 나온 경우를 충돌이라 부르며 해시충돌 해결방법에는 분리연결법과 개방주소법이 있다.
  • 분리연결법은 셀에 하나의 값을 넣는 대신 배열로의 참조를 넣는 방식(Linked List)이다.
  • 개방주소법은 해시 충돌이 발생했을 때 충돌한 데이터를 새로운 빈 슬롯에 저장하는 방식이다.
    개방주소법에는 대표적으로 3가지가 있다.
    • Linear Probing: 현재의 index로부터 한칸씩 이동하여 비어 있는 버킷에 데이터를 저장
    • Quadratic Probing: 충돌횟수에 따라 $n^2$씩 index를 이동하여 비어있는 버킷에 저장
    • Double Hashing Probing: 충돌이 발생하면 그 값을 한번 더 해싱하여 데이터를 저장

해시테이블의 시간복잡도

• 읽기, 검색, 삽입, 삭제
  • key를 해시함수에 적용하여 만든 해시값을 버킷의 index로 사용하므로 해시충돌이 발생하지 않는다면 시간복잡도는 $O(1)$
  • 해시충돌이 지속적으로 발생하여 동일한 해시값에 여러 데이터들이 계속해서 연결된다면 시간복잡도는 $O(N)$에 수렴한다.

해시테이블의 활용 사례

• 데이터베이스에서의 인덱스 관리
• 파이썬의 딕셔너리(dict), 자바의 HashMap

---

6 . 트리 (Tree)

데이터 사이의 계층 관계를 표현하는 자료구조

• 트리는 그래프의 한 종류이다. (모든 트리는 그래프이지만, 그래프가 모두 트리는 아니다.)
• 트리는 아래 그림과 같이 노드와 가지로 구성된다. 노드는 가지를 통해 다른 노드와 연결된다.
• 트리는 방향성이 있는 비순환 그래프이다. (이부분에 대해선 다음 그래프 부분에 다룸)

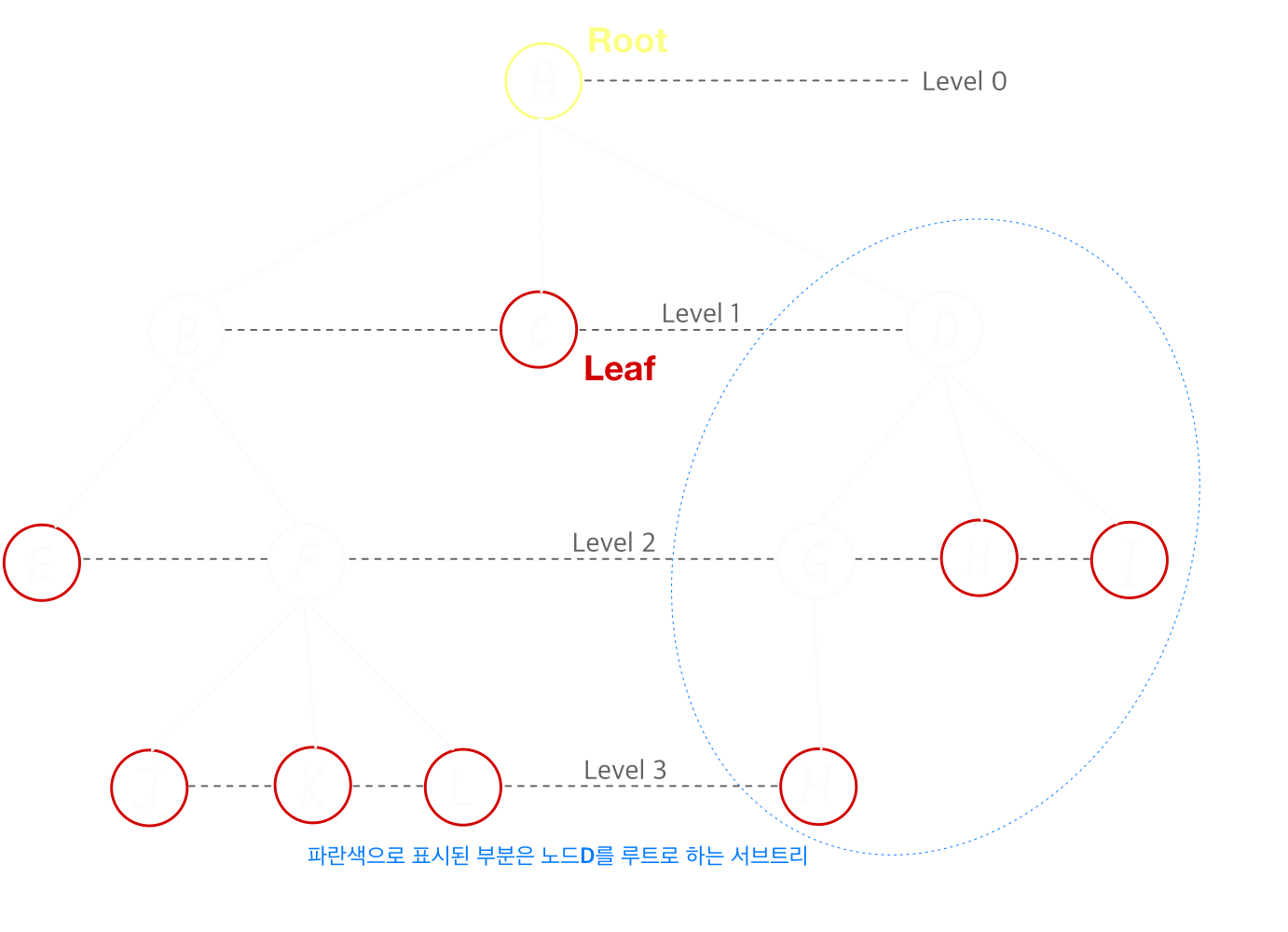
• 트리 용어

  • 루트(root): 트리의 가장 위쪽에 있는 노드, 루트는 트리 하나에 1개만 존재 (노란 노드)
  • 리프(leaf): 트리의 가장 아래쪽에 있는 노드, 가지가 더이상 뻗어나갈 수 없는 마지막 노드 (빨간 노드)
  • 자식(child): 어떤 노드와 가지가 연결되어 있을 때 아래쪽에 있는 노드 (E와 F는 B의 자식노드)
  • 부모(parent): 어떤 노드와 가지가 연결되어 있을 때 위쪽에 있는 노드 (F는 J, K, L의 부모노드)
  • 형제(sibling): 부모가 같은 노드 (G, H, I는 형제노드)
  • 레벨(level): root에서 얼마나 떨어져 있는지 나타냄 (root는 level 0)
  • 차수(degree): 각 노드가 갖는 자식의 수 (B의 차수는 2, G의 차수는 1)
    모든 노드의 차수가 n이하인 트리를 n진트리라 한다. 따라서 위 트리는 삼진트리
    모든 노드의 자식이 2개이하면 이진트리

트리의 시간 복잡도

1. 이진 탐색 트리 (Binary Search Tree):
   • 탐색, 삽입, 삭제:
     • 최악의 경우 트리가 편향될 수 있어 $O(N)$
     • 트리가 균형을 이루면 $O(log N)$
2. AVL 트리 (자기 균형 이진 탐색 트리):
   • 탐색, 삽입, 삭제: 항상 균형을 유지하여 $O(log N)$
3. 힙(Heap):
   • 삽입, 삭제: $O(log N$)
   • 최댓값/최솟값 접근: $O(1)$

트리 탐색 알고리즘

• DFS/BFS: 모든 노드를 한 번씩 방문하므로 시간 복잡도는 $O(N)$
  

트리 순회(Traversal)의 종류

• 전위(pre-order): Root → Left → Right
• 중위(in-order): Left → Root → Right (이진 탐색 트리에서 오름차순 정렬 결과)
• 후위(post-order): Left → Right → Root

트리의 활용 사례

• 파일 시스템의 디렉토리 구조
• HTML/XML의 DOM 구조

---

7. 그래프 (Graph)

그래프는 노드와 노드를 연결하는 간선으로 이루어진 자료구조

• 정점(Vertex): 데이터를 저장하는 위치 (노드)
• 간선(Edge): 두 정점을 연결하는 선, 관계를 나타냄
• 그래프는 방향성과 순환성 여부에 따라 여러 유형으로 나뉨
  • 무방향 그래프: 간선에 방향이 없음
  • 방향 그래프: 간선에 방향이 존재
  • 순환 그래프: 순환하는 경로가 존재
  • 비순환 그래프(DAG): 순환하지 않음
• 그래프는 네트워크, 소셜 네트워크, 도로망 등 다양한 응용에서 사용

그래프의 시간 복잡도

1. 탐색 시간 복잡도
   • 정점 탐색: 각 정점을 한 번씩 방문하므로 $O(V)$
   • 간선 탐색: 무방향 그래프는 간선을 두 번 탐색, 방향 그래프는 한 번씩 탐색하여 $O(E)$
   • 전체 시간 복잡도 $O(V + E)$
2. 그래프 구현 방식에 따른 차이
   • 인접 행렬: 정점 간 연결 정보를 2차원 배열로 저장. 탐색 시간 복잡도는 O(V^2)
   • 인접 리스트: 정점마다 연결된 정점을 리스트로 저장. 탐색 시간 복잡도는 O(V + E)
3. 특정 알고리즘 시간 복잡도
   • 다익스트라 알고리즘: $O((V + E) log V)$
   • 프림 알고리즘: $O((V + E) log V)$

유명한 그래프 알고리즘

• 다익스트라(Dijkstra) 알고리즘: 최단 경로 탐색
• 프림(Prim), 크루스칼(Kruskal) 알고리즘: 최소 신장 트리(MST)
• 플로이드-와샬(Floyd-Warshall) 알고리즘: 모든 정점 간 최단 거리 계산

그래프의 활용 사례

• 소셜 네트워크 분석
• 내비게이션의 경로 탐색
• 웹 페이지의 링크 구조 분석