K-MOOC 1회차 - Recursion (재귀)
Recursion - 재귀
재귀함수
- 자기 자신을 호출하는 함수
재귀적 방법
- 자기자신을 호출하는데 반복되는 함수가 자신보다 범위가 좁은 함수를 호출하는 방법
- 자기 자신을 쪼개서 문제를 해결합니다(Reduction)
- 반복하여 재귀가 돌아가며, 특정 지점에 도달하면 재귀가 종료되며 값들이 역으로 반환됩니다.
- Recursion은 Recursive case와 Base case로 구성되어 있습니다.
재귀를 사용하는 이유
- 코드가 간편하다.
- 정렬, 탐색, 선택 알고리즘의 경우에 Recursion으로 쉽게 해결 가능 하다.
💡 Recursion
- Base Case인 경우 Recursion이 종료됩니다.
- Recursion을 반복해서 실행할 수록 추가적인 메모리 공간을 요구합니다.
- 무한 Recursion에 빠지게 된다면 결국 스택 오버플로우가 발생하게 됩니다.
- 어려운 문제들의 경우에 Recursion을 사용하여 쉽게 해결 가능합니다.
💡 Loop(for, while)
- 조건이 거짓일 경우에 Loop가 종료됩니다.
- Loop를 반복해서 실행 하더라도 추가적인 메모리 공간을 요구하지 않습니다.
- 무한 Loop에 빠지게 되더라도 스택 오버플로우는 발생하지 않습니다.
- 어려운 문제들의 경우에 Recursion에 비해 쉽게 해결되지 않을 수 있습니다.
Recursion의 참고사항
- Recursion은 Base Case와 Recursive Case 2 종류로 이루어져 있습니다.
- 무조건 Base Case에서 Recursion이 종료되어야 합니다. (종료되는 지점이 반드시 있어야 합니다.)
- 보통 Loop가 Recursion보다 효율적입니다. (Recursion은 스택이 쌓일 때 마다 추가 메모리를 요구하기 때문입니다.)
- Recursion으로 해결되는 문제의 경우, Loop로도 해결되는 경우가 있습니다.
- 문제에 따라서 최적의 해결 방식이 다릅니다.
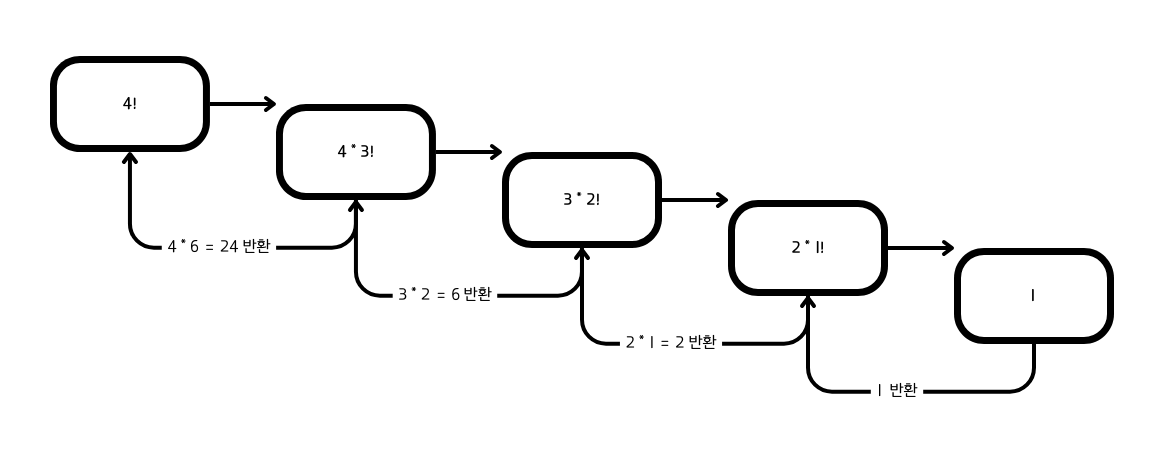
Recursion 활용 알고리즘 1 - 팩토리얼
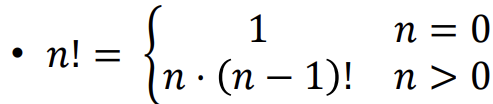
void fact(int n) {
if(n == 0) { //base case
return 1;
}
else { //recursive case
return n * fact(n-1);
}
}