분할 정복 알고리즘

---

어려운 문제를 해결하기 위해 Recursion을 사용하여 여러 문제로 쪼갠 다음 다시 합치는 문제 해결 알고리즘이다.

문제를 나눠 해결함으로써 어려운 문제를 쉽게 해결하고 알고리즘의 시간복잡도를 최적의 값으로 만들기 위해 쓰인다.

D&C의 pattern

---

Divide : 문제에서 주어진 인스턴스를 여러개로 동일하게 갈라진 독립적이고 작은 인스턴스로 분할한다.

Delegate : 각각의 작은 인스턴스를 Recursion을 통해 대신 연산을 수행한다.

Combine : 작은 인스턴스들에 대한 solution을 주어진 인스턴스들의 최종 solution 으로 결합한다.

Divide-and-Conquer를 사용하는 알고리즘 1 : Mergesort(평균:O(n log n), 최악:O(n^2))

---

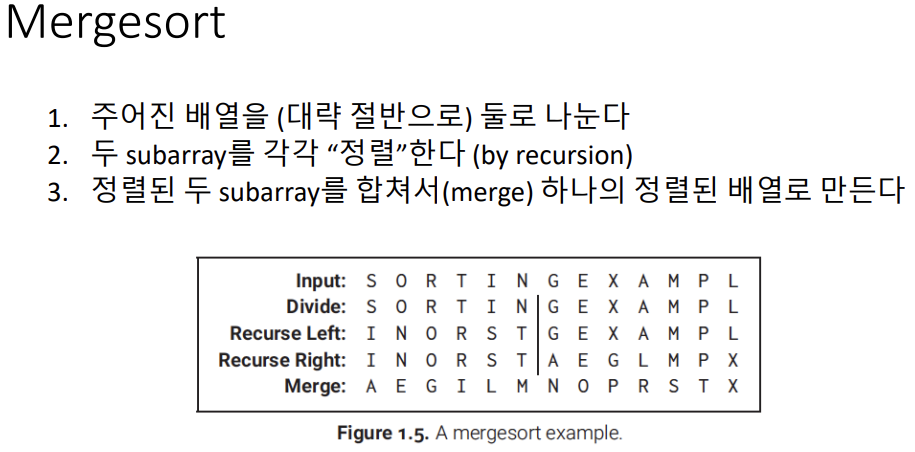
Mergesort의 pseudocode

MergeSort(A[1…n]):
if n > 1
    m ← ⌊n/2⌋
    MergeSort(A[1…m])         //Recurse
    MergeSort(A[m+1…n])       //Recurse
    Merge(A[1..n, m)

Merge(A[1…n], m):
    i ← 1; j ← m + 1
    for k ← 1 to n
        if j > n
            B[k] ← A[i]; i← i + 1
        else if i > m
            B[k] ← A[j]; j ← j + 1
        else if A[i] < A[j]
            B[k] ← A[i]; i ← i + 1
        else
            B[k] ← A[j]; j ← j + 1
    for k ← 1 to n
        A[k] ← B[k]

Divide-and-Conquer를 사용하는 알고리즘 2 : Quicksort(평균:O(n log n), 최악:O(n^2))

---

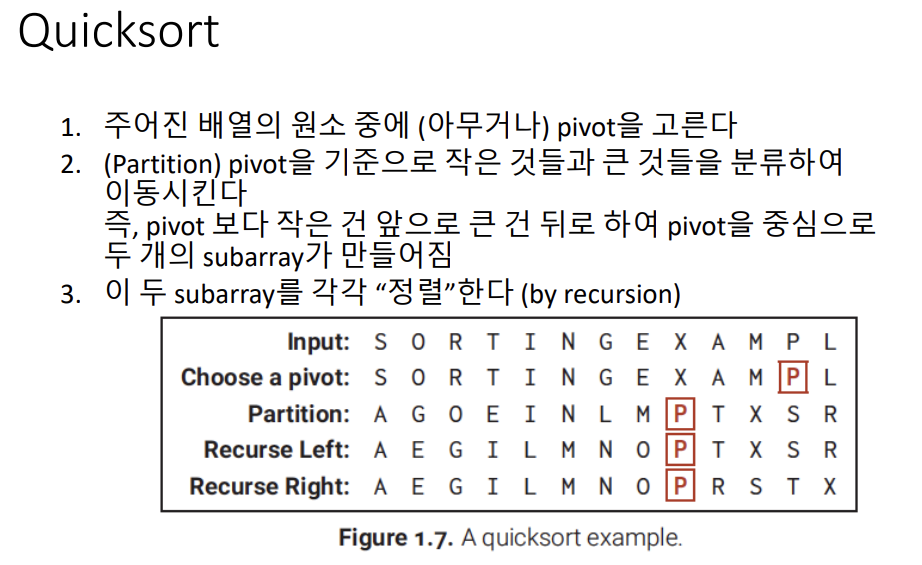
Quicksort의 pseudocode

QuickSort(A[1…n]):
    if(n > 1)
        Choose a pivot element A[p]
        r ← Partition(A, p)        //pivot의 idx
        QuickSort(A[1…r-1])        //Recurse
        QuickSort(A[r + 1…n])      //Recurse

Partition(A[1…n], p):
    Partition(A[1…n], p):
    swap A[p] ↔ A[n]
    l ← 0        //작은 값이 스왑되는 자리
    for i ← 1 to n - 1
        if A[i] < A[n]
            l ← l + 1
            swap A[l] ↔ A[i] //작은 값을 앞으로 당김
    swap A[n] ↔ A[l + 1]
    return l + 1